Rotation runt y axeln
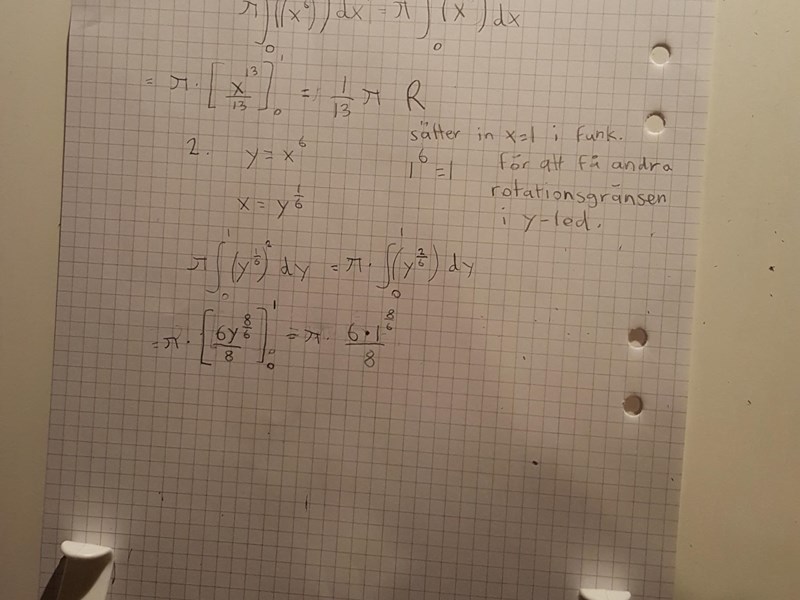
Jag ska rotera y=x^6 som avgränsas av y=0 och x=1 runt y axeln. Vad blev fel?
Elias93 skrev:
Jag ska rotera y=x^6 som avgränsas av y=0 och x=1 runt y axeln. Vad blev fel?
Felet är att du inte har ritat en figur så att du har klart för dig vilken integrationsmetod du ska använda eller hur volymelementet ser ut.
Du har integrerat i x-riktning som om du skulle använda skalmetoden men av din integrand att döma verkar du använda skivmetoden.
-------------
EDIT - jag trodde att även din första uträkning gällde samma uppgift, men om den handlar om rotation kring x-axeln så är den rätt.
Din andra uträkning är rätt.
Jag tycker det ser rätt ut. blir 1, så den kan du ta bort.
Min lärobok är på engelska, vad betyder skalmetod och skivmetod? Jag har bara hittat en formel i boken för att vara ärlig och en förklaring till den. Den beskriver volymen som en basarea som är cirkulär och sen lägger man till många skivor med bredden deltax. Sen finns det ett exempel där ska rotera runt y axeln men då löser de bara ut y ur funktionen och kör samma formel.
Varför tror du att det blev fel?
enligt facit är det fel och yngve vet något som kan hjälpa
Det är två olika uppgifter. Men enligt facit är andra uppgiften fel
Hej!
Du har inte talat om om det är en rotationsvolym eller en rotationsarea som ska beräknas; bara för att det är en "rotationsuppgift" så behöver det inte automatiskt handla om volym.
Beräkna den volym som erhålls då området i R^2 som begränsas av
y=0, y=x^6 och x=1 roteras runt y axeln
Elias93 skrev:Det är två olika uppgifter. Men enligt facit är andra uppgiften fel
Kan du låta oss få veta vad som står i facit?
Nu hittade jag en annan formel. Jag ska läsa på ordentligt nästa vecka om hur man vet vilken av dem man ska använda. 2Pi/8 var rätt
Elias93 skrev:Min lärobok är på engelska, vad betyder skalmetod och skivmetod? Jag har bara hittat en formel i boken för att vara ärlig och en förklaring till den. Den beskriver volymen som en basarea som är cirkulär och sen lägger man till många skivor med bredden deltax. Sen finns det ett exempel där ska rotera runt y axeln men då löser de bara ut y ur funktionen och kör samma formel.
Jag missuppfattade din fråga och har korrigerat mitt svar.
Det du beskriver är skivmetoden, där rotationskroppen delas upp i ett stort antal cirkulära skivor som är vinkelräta mot rotationsaxeln. Varje skiva har arean , där radien beror på skivans position längs med rotationsaxeln. Integrationsriktningen är längs med rotationsaxeln.
Skalmetoden går ut på att rotationskroppen istället delas upp i ett stort antal cylindriska skal runt rotationsaxeln. Varje skal har en mantelarea som är , där är avståndet från rotationsaxeln och är skalets höjd. Integreringen sker då i radiell riktning ut från rotationsaxeln.
Elias93 skrev:Beräkna den volym som erhålls då området i R^2 som begränsas av
y=0, y=x^6 och x=1 roteras runt y axeln
Då är rätt svar a.e.
EDIT -många fel i samma svar här. Varken mätetal eller enhet blev rätt.
Hej!
Om du ritar en figur om problemet så ser du att den sökta volymen (den blå volymen) kan uppfattas som en differens mellan två volymer: Cylindern med radie 1 och höjd 1, samt volymen som fås när kurvan med roterar kring -axeln.
Cylinderns volym är och kurvans volym är där så den sökta volymen är
Yngve skrev:Elias93 skrev:Beräkna den volym som erhålls då området i R^2 som begränsas av
y=0, y=x^6 och x=1 roteras runt y axelnDå är rätt svar a.e.
Men inte areaenheter.
Jag missade att volymen begränsades av y = 0, jag trodde det var y = 1.
Laguna skrev:Jag missade att volymen begränsades av y = 0, jag trodde det var y = 1.
Jag med.
Laguna skrev:
Men inte areaenheter.
Varken areaenheter elle tre pi genom fyra var rätt.
Albiki skrev:Hej!
Om du ritar en figur om problemet så ser du att den sökta volymen (den blå volymen) kan uppfattas som en differens mellan två volymer: Cylindern med radie 1 och höjd 1, samt volymen som fås när kurvan med roterar kring -axeln.
Cylinderns volym är och kurvans volym är där så den sökta volymen är
Beräknas integralen bör man få den sökta volymen



