Rotationsarea

Här gäller det att inte vara för snabb med krångliga variabelbyten. Vad händer om vi multiplicerar ihop rötterna?

$\displaystyle 4\pi \int_{0}^{21} \sqrt{7y}\sqrt{1+\frac{7}{y}}\ dy=4\pi \int_{0}^{21} \sqrt{7y(1+\frac{7}{y})}\ dy=4\pi \int_{0}^{21} \sqrt{7y+49}\ dy=...$

Ok, jag ska försöka innan jag ropar på dig.

$$\begin{gathered} \sqrt{7y+49}= t \\ dt=\frac{1}{2\sqrt{7y+49}}dy \iff dy=\frac{dt}{2t} \end{gathered}$$

Integralen blir...

 $$\begin{gathered} 4\mathrm{\pi } \frac{1}{2}\int \frac{2dt}{2t} \leftrightarrow \frac{1}{2}\ln \left|2t\right| = \\ 2\mathrm{\pi } \ln \left|2\sqrt{7y+49}\right| \end{gathered}$$

?

Nja, inte riktigt daja, om

$t=\sqrt{7y+49}$

blir ju derivatan

$\dfrac{dt}{dy}=\dfrac{7}{2\sqrt{7y+49}}$

$dt=\dfrac{7}{2t}\ dy$

$dy=\dfrac{2t}{7}\ dt$

Annars kan jag rekommendera en substitution med lite roligare siffror, $t=7y+49$, alltså bara det som står i roten, utan själva roten.

Orright.

$$\begin{gathered} t=7y+49 \\ dy=\raisebox{1ex}{$dt$}\!\left/ \!\raisebox{-1ex}{$7$}\right. \end{gathered}$$

$$\begin{gathered} \frac{4\mathrm{\pi }}{7}{\int }_0^{21}\sqrt{t}dt = \frac{{\displaystyle 2·4\mathrm{\pi }}}{{\displaystyle 3·7}}{\left[t^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right]}_0^{21} \iff \\ \frac{{\displaystyle 8\mathrm{\pi }}}{{\displaystyle 21}}{\left[{\left(7y+49\right)}^{3/2}\right]}_0^{21} =\frac{{\displaystyle 8\mathrm{\pi }}}{{\displaystyle 21}}\left[{\left(7·21+49\right)}^{3/2}-{49}^{3/2}\right]= \\ \frac{{\displaystyle 8\mathrm{\pi }}}{{\displaystyle 21}}\left[{196}^{3/2}-{49}^{3/2}\right]=\frac{{\displaystyle 8\mathrm{\pi }}}{{\displaystyle 21}}\left[{14}^3-7^3\right] \end{gathered}$$

Yes, det är rätt!

Även om jag klantrade mig på förkortning nånståns...

dajamanté skrev:

...

Även om jag klantrade mig på förkortning nånståns...

Klantrade, kantrade eller klantade?

Du är väl inte ute och seglar igen Daja? 😉

Det ser ut som min processor kan focca på BARA ett ämne :)

Jag kantrade på faktorisering.

Finns det ett bättre sätt? Jag tror faciten föreslår 56pi delat med något.

Vad säger facit?

Det mest förenklade jag kan få det till är:

$\dfrac{2744\pi}{3}$

Den säger: 

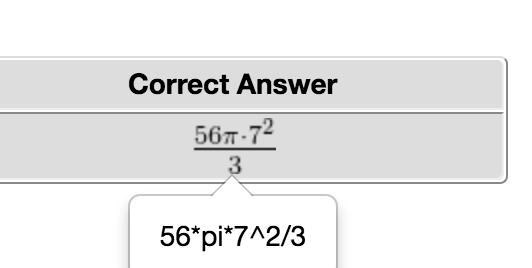
Så samma som din, bara primtalfaktoriserad. Jag vet inte varför jag trodde nåt annat. Tack för hjälpen 🌷🌷

edit: vänta ett tag, jag tror jag vet vad dem tar den 56 ifrån.. dem kanske använder sig av den här shell metoden eller hur?

$2\mathrm{\pi }{\int }_a^b\mathrm{xy} \mathrm{dx}$ 

$y=\frac{x^2}{28}, när y=21 x=14\sqrt{3}$

$$\begin{gathered} 2\mathrm{\pi }{\int }_0^{14\sqrt{3}}x \frac{x^2}{28} \mathrm{dx} \\ 2\mathrm{\pi }{\left[\frac{x^4}{4·28}\right]}_0^{14\sqrt{3}}=.... \end{gathered}$$

Det blir inga trean i nämnaren men det är säkert en av mina slarv?

edit 2: glöm det part 2.

det ifrågas en area och inte en volym....