Rotationskroppar
Jag behöver hjälp med den här uppgiften:
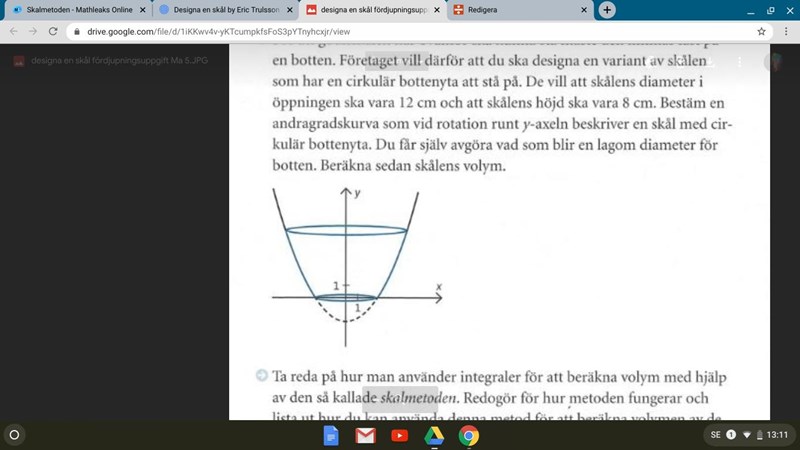
För att godisskålen här ovan ska kunna stå behöver den en botten. Företaget vill därför att du ska designa en variant av skålen som har en cirkulär bottenyta att stå på. De vill att skålens diameter i öppningen ska vara 12 cm och att skålens höjd ska vara 8 cm. Bestäm en andragradskurva som vid rotation med y-axeln beskriver en cirkulär bottenyta. Du får själv avgöra vad som blir en lagom diameter för botten. Beräkna sedan skålens volym.
Jag vet inte hur jag ska börja på uppgiften, vad kan jag göra?
Det låter som om det hör en bild till uppgiften.
Kan du ange en andragradsfunktion som ser ut så?
Nej, jag har problem med det. Jag har valt diametern 2, alltså måste den rotera mellan x=1 och x=-1.
Vilken är symmetrilinjen för andragradskurvan?
bx/2, den går mellan nollställena.
Supernova127, det räcker med en tråd om den här uppgiften - det står i Pluggakutens regler. Jag har tagit bort din dubbelpost. /moderator
Men den där frågan handlade om en annan skål som inte har en"fot". Det där var en annan deluppgift.
Vilket värde har b i den allmänna formeln för andragradsfunktionen om symmetrilinjen är som i den här bilden?
Jag testade att göra det här eftersom jag förstod inte hur jag skulle göra med b. Eftersom nollställena är (-1,0) och (1,0) så borde ekvationen kunna skrivas som y = (x+1)(x-1)=x²+1.
Stämmer det?
Med b körde jag fast här: bx/2 = 0. Ska x istället vara 0?
Borde inte b ha värdet 0 eftersom symmetrilinjen går vid x=0?
Det stämmer att b har värdet 0 eftersom symetrilinjen är x = 0. Kan du hitta en funktion f(x)=ax2+c där f(1) = 0(eftersom du valde att bottendiametern skulle vara 2 cm) och f(6)=8 (eftersom skålen skulle ha diametern 12 cm i toppen och skulle vara 8 cm hög)?
Jag får ekvationen till: f(x) = .
Så här får jag fram det: f(1) = 0
0 = a*1 +c
0 = a + c
-c = a
8 = a * 6^2 + c
8 = 36a +c
8 = 36(-c) + c
8 = -36c + c
8 =-35c
=c
a =
Gör jag rätt?
Rita upp din kurva och kolla att den stämmer. Lägg upp bilden här.
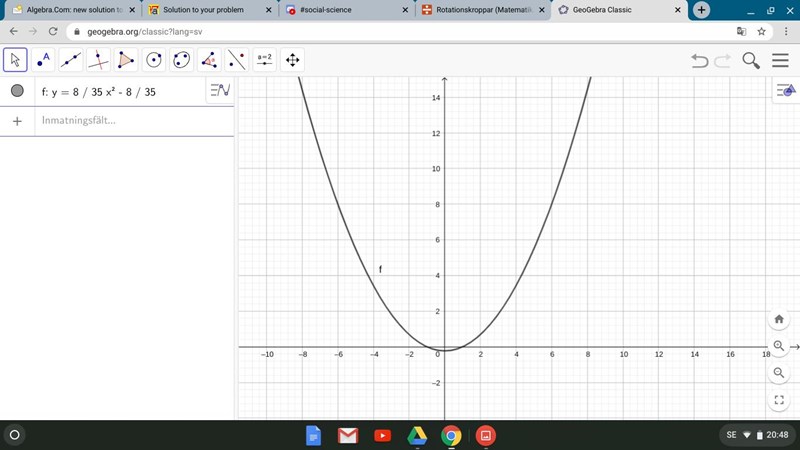
Hur vet jag om den stämmer?
Den stämmer i punkterna och , det räcker.
Beräkna nu skålens volym.

Såhär gör jag det, är det korrekt och tydligt hur jag tänker?
Nej det stämmer inte. Din volym är negativ, vilket inte stämmer.
Jag föreslpr att du delar upp skålen i två olika delar:
A - En rak cirkulär cylinder med diameter b - a i mitten av skålen. Volymen av denna kan du enkelt beräkna med en formel.
B - En del utanför cylindern, där skålens väggar är parabelformade. Volymen av denna kan du integrera fram med hjälp av skalmetoden. Men du bör då först rita upp ett skal på avstånd r från y-axeln och skriva uttryck dels för radien och dels för hur stor area skalet har.
Ungefär så här (rotat på en skakig bussfärd):
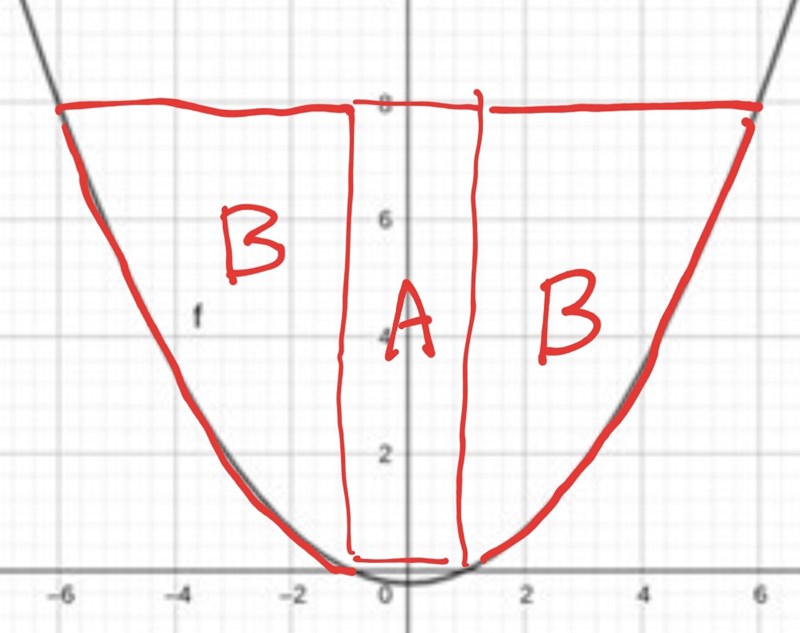

Såhär??
Nej. Vilka är integrationsgränserna för andragradsfunktionen?
Supernova127 skrev:
Såhär??
Cylindervolymen är nästan rätt, men cylindern har höjden 8, inte 12.
Vad gäller den andra volymen, kan du berätta hur du kom fram till den integranden (dvs den funktion du integrerar)?
Vad gäller integrationsgränserna så är de nu nästan rätt, men inte riktigt. Du ska integrera från den innersta radien till den yttersta radien i område B.
Vad är den innersta och yttersta?
Jag får funktionen till: f(x) = 835x²−835835x²-835.
Så här får jag fram det: f(1) = 0
0 = a*1 +c
0 = a + c
-c = a
8 = a * 6^2 + c
8 = 36a +c
8 = 36(-c) + c
8 = -36c + c
8 =-35c
−8/35 =c
a = 8 /35
b = 0 eftersom symmetrilinjen är vid x = 0.
Supernova127 skrev:Vad är den innersta och yttersta?
Jag får funktionen till: f(x) = 835x²−835835x²-835.
Jag antar att du menar , som du skrev i det här svaret.
Men den funktionen beskriver inte skålens djup (h i figuren) utan istället avståndet från skålens undersida ner till bordet (a i figuren). Så den volym du försöker beräkna är hur mycket luft det finns under skålen.
Du ser bu hur viktigt det är att rita en figur som visar hur skålen och skalen ser ut och med hjälp av den ta fram ett uttryck för skalens höjd. Detta uttryck ska vara lika med skålens djup.
Gör nu det och visa oss ditt försök.
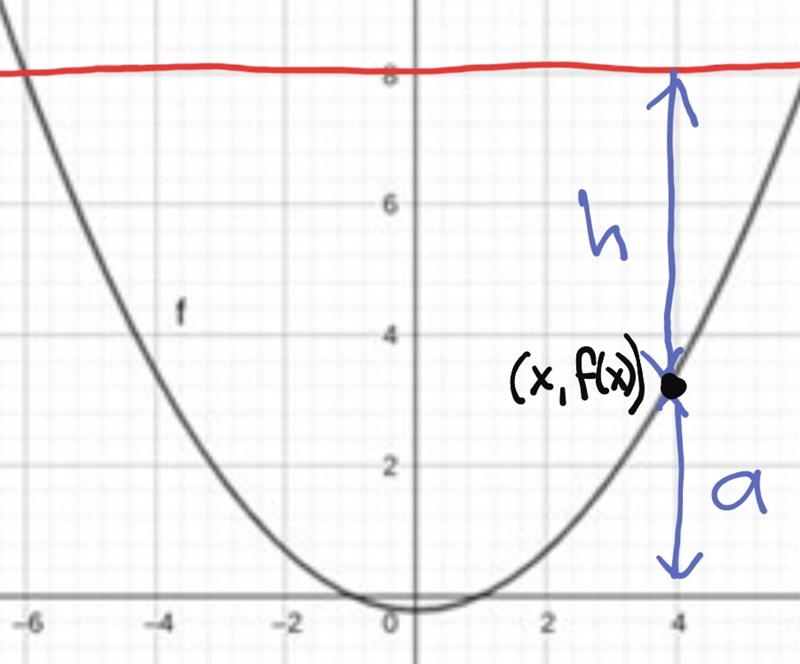
Det här är det jag nu har kommit fram till:
.jpg?width=800&upscale=false)
Jag förstår inte vad V står för och jag ser inte hur integranden ser ut.
Är den första faktorn beroende av y och den andra av x?
Varför integrerar du nu i y-led, skulle du inte använda skalmetoden med en radie i x-led?
Kan du berätta hur du har tänkt? Visa gärna din figur så blir det lättare att beskriva din tankegång.
Den ovan var fel, det här är det jag nu kommit fram till.
V =
Jag kollade på en youtube film som hade liknade problem som mig
Supernova127 skrev:Den ovan var fel, det här är det jag nu kommit fram till.
V =
Jag kollade på en youtube film som hade liknade problem som mig
Nu integrerar du tydligen i y-led. Det är bra, för det blir enklare. Men det är inte rätt. Hur lyder den generella formeln i det fallet?
Jag löste uppgiften, tack!
Tjena skulle du kunna skicka hela din lösning
Kevin7 skrev:Tjena skulle du kunna skicka hela din lösning
Hej och välkommen till Pluggakuten!
Anvöndaren Supernova127 är inte längre kvar här på Pluggakuten.
Skapa en ny tråd och visa hur långt du kommer med uppgiften så får du snabba och bra svar.
Det är samma uppgift undrade om vem som hälsa kan bara visa mig hur man börjar :)
Kevin7 skrev:Det är samma uppgift undrade om vem som hälsa kan bara visa mig hur man börjar :)
En bra början ser du i svar #15 i denna tråd.
Vad vet du om metoder för att beräkna volymen av rotationskroppar?
Du får fler och snabbare svar om du startar en ny tråd och visar dina försök. Den här tråden är klarmarkerad (grön), så den väcker inte så mycket uppmärksamhet.
Hej!
jag förstår hela uppgiften men förstår inte hur man räknar ut K i formen Y=KX^2?
vad står K för och vad är stegen för att räkna ut det?
Hejsan44 skrev:Hej!
jag förstår hela uppgiften men förstår inte hur man räknar ut K i formen Y=KX^2?
vad står K för och vad är stegen för att räkna ut det?
Hej och välkommen till Pluggakuten!
I en parabel y = k•x2 så står konstanten k för
- "riktningen": k > 0 ger "glad mun" (dvs parabel som ser ut som ett U) och k < 0 ger "ledsen mun" (dvs parabel som ser ut som ett uppochnervänt U)
- "skålningen"/"brantheten": Stort värde på |k| ger kraftigt skålad parabel, litet värde på |k| ger en parabel som mer ser ut som ett fat.
Du kan bestämma värdet på k genom att känna till tre punkter på parabeln. Om du känner till vertex så räcker det med en annan punkt.
=====
Om du behöver mer hjälp så får du fler och snabbare svar om du startar en ny tråd och frågar där. Den här tråden är klarmarkerad (grön), så den väcker inte så mycket uppmärksamhet.
Okej förstår men hur räknar man ut k genom att känna till 3 punkter i parabeln. Om man hittar ett X värde och ett Y värde borde det inte räcka för att räkna ut k?
Hejsan44 skrev:Okej förstår men hur räknar man ut k genom att känna till 3 punkter i parabeln. Om man hittar ett X värde och ett Y värde borde det inte räcka för att räkna ut k?
Jo, du har rätt (om det inte är origo som är den enda kända punkten).
Om vi t.ex. känner till punkten (2, -8) så vet vi att konstanten k ska uppfylla villkoret -8 = k•22, vilket ger oss att k = -2.
Jag tänkte på en generell andragradsfunktion på formen y = ax2+bx+c. Då behövs det tre punkter.