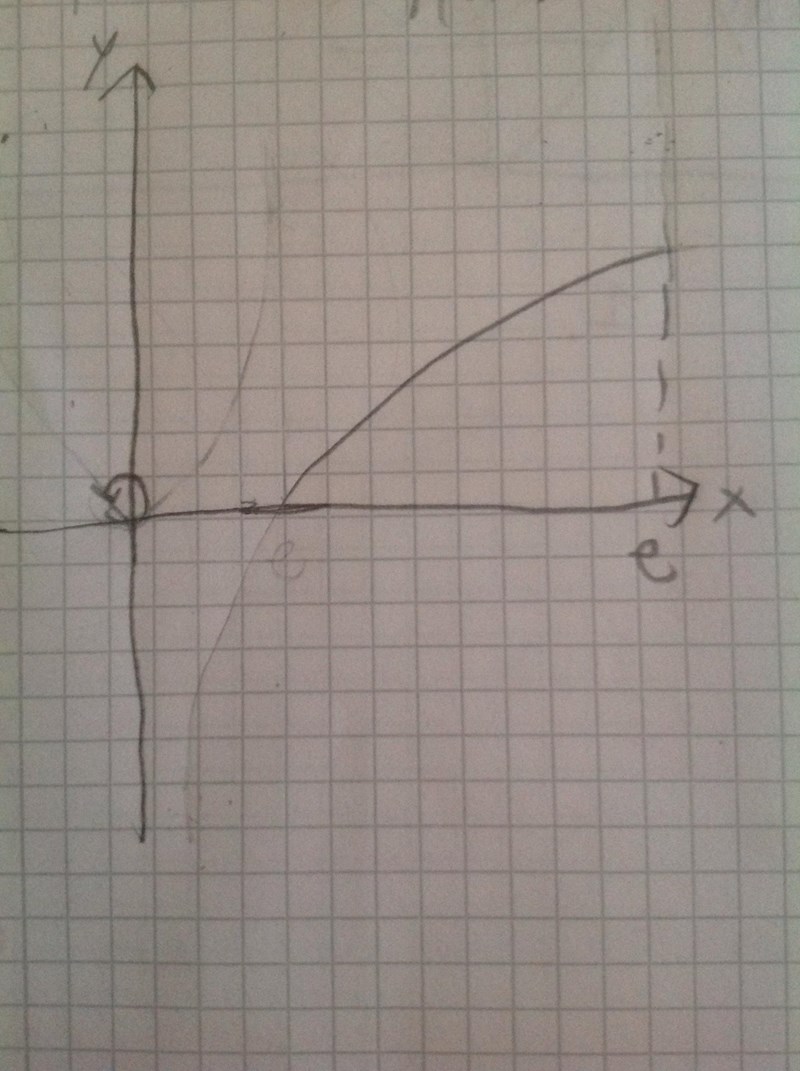
Rotationsvolym kring y-axel (Matematik/Matte 4/Integraler och tillämpningar)

lamayo skrev:
Låt det område som begränsas av kurvan y=lnx, linjen x=e samt x-axeln rotera kring y-axeln. Bestäm volymen av den uppkomna rotationskroppen.
Jag gjorde följande men får fram fel: x=e^y, y=1.
$π \int_{0}^{1} (e^2 y) dy = pi [2 e^2 y] 0 till 1 .$ Går det fel redan här? Försökt felsöka men ser inte vart det går fel?
Tacksam för hjälp

Det är nog så att du räknar ut fel volym. du får fram volymen som uppstår mellan ln(x) och y-axeln, men man frågar efter volymen som uppstår mellan ln(x) och x-axeln.

Rita din kurva och markera vilken yta det är som roterar så inser du.

Så du får subtrahera din uträknade volym från den cylinder som uppstår när x=e roterar runt y-axeln. Eller använda skalmetoden.

Dessutom är din primitiva funktion fel!

lamayo skrev:
Låt det område som begränsas av kurvan y=lnx, linjen x=e samt x-axeln rotera kring y-axeln. Bestäm volymen av den uppkomna rotationskroppen.
Jag gjorde följande men får fram fel: x=e^y, y=1.
$π \int_{0}^{1} (e^2 y) dy = pi [2 e^2 y] 0 till 1 .$ Går det fel redan här? Försökt felsöka men ser inte vart det går fel?
Tacksam för hjälp

Följ denna checklista och beskriv varje steg för oss så kan vi hjälpa dig bättre:

1. Rita figur, förstå vad de frågar efter.

2. Bestäm områdets gränser.

3. Välj integrationsmetod (skalmetoden/skivmetoden).

4. Finn ett uttryck för volymselementet dV.

5. Bestäm integrationsgränserna (från punkt 3).

6. Integrera.

7. Kontrollera/rimlighetsbedöm svaret.

Yngve skrev:
lamayo skrev:
Låt det område som begränsas av kurvan y=lnx, linjen x=e samt x-axeln rotera kring y-axeln. Bestäm volymen av den uppkomna rotationskroppen.
Jag gjorde följande men får fram fel: x=e^y, y=1.
$π \int_{0}^{1} (e^2 y) dy = pi [2 e^2 y] 0 till 1 .$ Går det fel redan här? Försökt felsöka men ser inte vart det går fel?
Tacksam för hjälp
Följ denna checklista och beskriv varje steg för oss så kan vi hjälpa dig bättre:
1. Rita figur, förstå vad de frågar efter.
2. Bestäm områdets gränser.
3. Välj integrationsmetod (skalmetoden/skivmetoden).
4. Finn ett uttryck för volymselementet dV.
5. Bestäm integrationsgränserna (från punkt 3).
6. Integrera.
7. Kontrollera/rimlighetsbedöm svaret.

lamayo skrev:

Toppen att du ritar grafer och visar!

Det blir så mycket enklare för oss att hjälpa dig då.

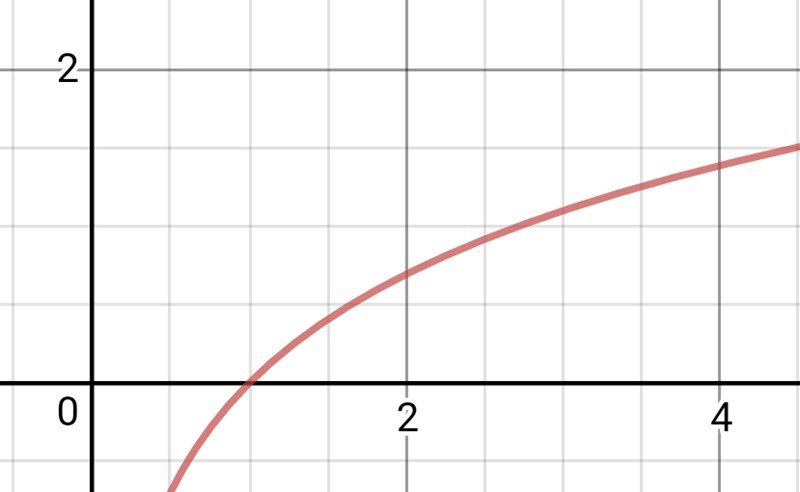
Grafen till y = ln(x) ser ut så här:

Yngve skrev:
lamayo skrev:
Toppen att du ritar grafer och visar!
Det blir så mycket enklare för oss att hjälpa dig då.
Grafen till y = ln(x) ser ut så här:

lamayo skrev:

Ja nu ser det bra ut. Vid vilken x-koordinat nuddar kurvan x-axeln?

Det är alltså det blåmarkerade området som roterar runt y-axeln. Ser du framför dig hur det då bildas en rotationskropp?

Den ser ut som en solid cylinder med ett urgrävt hål i mitten.

Det blir alltså som en rund skål med vertikala ytterkanter, rundad innerkant och ett hål i den flata botten.

Nu kan du använda skalmetoden eller skivmetoden. Vilken av dem är du mest bekväm med?

De ger helt olika integraler att lösa. Ibland är den ena metoden enklare, ibland är den andra metoden enklare.

Försök att komma vidare nu och visa hur du tänker.

Yngve skrev:
lamayo skrev:
Ja nu ser det bra ut. Vid vilken x-koordinat nuddar kurvan x-axeln?
Det är alltså det blåmarkerade området som roterar runt y-axeln. Ser du framför dig hur det då bildas en rotationskropp?
Den ser ut som en solid cylinder med ett urgrävt hål i mitten.
Det blir alltså som en rund skål med vertikala ytterkanter, rundad innerkant och ett hål i den flata botten.
Nu kan du använda skalmetoden eller skivmetoden. Vilken av dem är du mest bekväm med?
De ger helt olika integraler att lösa. Ibland är den ena metoden enklare, ibland är den andra metoden enklare.
Försök att komma vidare nu och visa hur du tänker.

Jag har hört att skivmetoden är lättast vid rotationsvolym kring x-axel och skalmetoden är lättast vid rotationsvolymkring y-axel, stämmer det?

Nu borde jag väll ta reda på var funktionen skär x-axeln för att ta reda på integrationsgränserna? Ska jag sätta y=0 så derivera lnx och sätta det lika med 0, 1/x=0?

lamayo skrev: Jag har hört att skivmetoden är lättast vid rotationsvolym kring x-axel och skalmetoden är lättast vid rotationsvolymkring y-axel, stämmer det?

Det är inte alltid så. Det beror helt på hur området ser ut.

Detta problem går att lösa med skalmetoden, men min uppfattning är att att skivmetoden är enklare här.

Däremot går det inte att ta metoden "direkt från formel", så det är alltid otroligt viktigt att skaffa sig en bild av hur rotationsvolymen ser ut så att man inte råkar välja fel integrationsgränser eller fel funktion att integrera.

Nu borde jag väll ta reda på var funktionen skär x-axeln för att ta reda på integrationsgränserna? Ska jag sätta y=0 så derivera lnx och sätta det lika med 0, 1/x=0?

Ja du måste ta reda på var grafen skär x-axeln. Då grafen skär x-axeln är y-koordinaten lika med 0, är du med på det?

Alltså räcker det att lösa ekvationen y = 0, dvs ln(x) = 0 för att hitta det värde på x där kurvan skär x-axeln. Du behöver inte derivera.

Yngve skrev:
lamayo skrev: Jag har hört att skivmetoden är lättast vid rotationsvolym kring x-axel och skalmetoden är lättast vid rotationsvolymkring y-axel, stämmer det?
Det är inte alltid så. Det beror helt på hur området ser ut.
Detta problem går att lösa med skalmetoden, men min uppfattning är att att skivmetoden är enklare här.
Däremot går det inte att ta metoden "direkt från formel", så det är alltid otroligt viktigt att skaffa sig en bild av hur rotationsvolymen ser ut så att man inte råkar välja fel integrationsgränser eller fel funktion att integrera.
Nu borde jag väll ta reda på var funktionen skär x-axeln för att ta reda på integrationsgränserna? Ska jag sätta y=0 så derivera lnx och sätta det lika med 0, 1/x=0?
Ja du måste ta reda på var grafen skär x-axeln. Då grafen skär x-axeln är y-koordinaten lika med 0, är du med på det?
Alltså räcker det att lösa ekvationen y = 0, dvs ln(x) = 0 för att hitta det värde på x där kurvan skär x-axeln. Du behöver inte derivera.

Okej, hur vet jag vilken metod som är enklast?

Ja, den skär när x=1?

lamayo skrev:
Okej, hur vet jag vilken metod som är enklast?

Om du är ovan så föreslår jag följande: Du prövar den ena metoden fram till dess att det blir (för) krångligt. Då byter du och prövar den andra metoden och ser om det blir lättare så. Gör så nu och visa oss vad du gör/hur du resonerar.

Senare, när du har blivit van, så kommer du att redan på ett tidigt stadium i problemlösningen se vilken metod som är enklast.

Ja, den skär när x=1?

Ja det stämmer.

Yngve skrev:
lamayo skrev:
Låt det område som begränsas av kurvan y=lnx, linjen x=e samt x-axeln rotera kring y-axeln. Bestäm volymen av den uppkomna rotationskroppen.
Jag gjorde följande men får fram fel: x=e^y, y=1.
$π \int_{0}^{1} (e^2 y) dy = pi [2 e^2 y] 0 till 1 .$ Går det fel redan här? Försökt felsöka men ser inte vart det går fel?
Tacksam för hjälp
Följ denna checklista och beskriv varje steg för oss så kan vi hjälpa dig bättre:
1. Rita figur, förstå vad de frågar efter.
2. Bestäm områdets gränser.
3. Välj integrationsmetod (skalmetoden/skivmetoden).
4. Finn ett uttryck för volymselementet dV.
5. Bestäm integrationsgränserna (från punkt 3).
6. Integrera.
7. Kontrollera/rimlighetsbedöm svaret.

Vad menar du på 4. Finn ett uttryck för volymselementet dV?

Volymselementet är antingen en mycket tunn skiva (skivmetoden) eller ett mycket tunnt skal (skalmetoden). Ta fram ett uttryck för volymen av detta element som funktion av din integrationsvariabel.

lamayo skrev:Vad menar du på 4. Finn ett uttryck för volymselementet dV?

Kortfattat går skalmetoden ut på följande:

Dela in rotationskroppen i ett stort antal cylindriska skal runt rotationsaxeln. Varje skal har ett bestämt radiellt avstånd $r$ från rotationsaxeln, en omkrets $2\pi r$ , en höjd $h$ (som normalt beror av $r$ ), och en infinitesimal tjocklek $dr$ .

Volymselementet $dV$ har alltså volymen $2\pi rh$ $dr$ och den totala volymen $V$ är nu summan av bidragen från alla dessa volymselement. Denna summa kan beräknas som en integral där integrationen sker i radiell led från en inre radie $r_1$ till en yttre radie $r_2$ . Vid rotation kring y-axeln är $r=|x|$ , vid rotation kring x-axeln är $r=|y|$ .

Sök på Youtube för exempel.

----------------------------

Kortfattat går skivmetoden ut på följande:

Dela in rotationskroppen i ett stort antal skivor som alla har rotationsaxeln som centrum och en infinitesimal tjocklek $dx$ (eller $dy$ om skivorna är staplade på höjden).

Varje skiva har en bestämd radie $r$ (som beror av var i rotationskroppen skivan befinner sig), en area $\pi r^2$ och tjocklek $dx$ (eller $dy$ ).

Volymselementet $dV$ har alltså volymen $\pi r^2$ $dx$ (eller $\pi r^2$ $dy$ ) och den totala volymen $V$ är nu summan av bidragen från alla dessa volymselement. Denna summa kan beräknas som en integral där integrationen sker från undre gränsen $x_1$ till övre gränsen $x_2$ (eller från $y_1$ till $y_2$ ).

Sök på Youtube för exempel.

-------------------------

Är det då lite mer klart vad ett volymselement är?

Yngve skrev:
lamayo skrev:Vad menar du på 4. Finn ett uttryck för volymselementet dV?
Kortfattat går skalmetoden ut på följande:
Dela in rotationskroppen i ett stort antal cylindriska skal runt rotationsaxeln. Varje skal har ett bestämt radiellt avstånd $r$ från rotationsaxeln, en höjd $h$ som kan bero av $r$ , en omkrets $2\pi r$ och en infinitesimal tjocklek $dr$ .
Volymselementet har alltså volymen $2\pi r\cdot h dr$ och den totala volymen V är nu summan av bidragen från alla dessa volymselement. Denna summa kan beräknas som en integral där integrationen sker i radiell led från en inre radie $r_1$ till en yttre radie $r_2$ .
Sök på Youtube för exempel.
----------------------------
Kortfattat går skivmetoden ut på följande:
Dela in rotationskroppen i ett stort antal skivor som alla har rotationsaxeln som centrum och en infinitesimal tjocklek $dx$ (eller $dy$ om skivorna är staplade på höjden).
Varje skiva har en bestämd radie $r$ som beror av var i rotationskroppen skivan befinner sig, en area $\pi r^2$ och tjocklek $dx$ (eller $dy$ ).
Volymselementet har alltså volymen $\pi r^2 dx$ (eller $\pi r^2 dy$ ) och den totala volymen V är nu summan av bidragen från alla dessa volymselement. Denna summa kan beräknas som en integral där integrationen sker från undre gränsen $x_1$ till övre gränsen $x_2$ (eller från $y_1$ till $y_2$ ).
Sök på Youtube för exempel.
-------------------------
Är det då lite mer klart vad ett volymselement är?

Tack , känns som det klarnade lite. Det är alltså om man tex delar upp en volym i skivor med tex cylindrar, då är det varje cylinders volym? pi*r^2 dy är volymselemtet?

$π \int_{1}^{e} (lnx)^2 dy$ får följande om jag använder skivmetoden? lnx motsvarar väll funktionen f(x)?

lamayo skrev:
Tack , känns som det klarnade lite. pi*r^2 dy är volymselemtet?
$π \int_{1}^{e} (lnx)^2 dy$ får följande om jag använder skivmetoden? lnx motsvarar väll funktionen f(x)?

Det är när du kommer hit som det är så ofantligt viktigt att du har ritat en figur och att du förstår hur rotationskroppen ser ut. Du blandar ihop det hela lite grann vilket tyder på att du inte har ritat din figur helt klart. Se förslag längst ner.

---------------------------

Om du använder skalmetoden: Rotationen sker kring y-axeln. Se framför dig (eller försök rita) ett cylindriskt skal runt y-axeln på avståndet $r$ (dvs $$x$) från y-axeln. Detta skal har en omkrets som är $$2\pi r $, dvs$ 2\pi x$$, en höjd $$h$$ som är $$ln(x)$$ och en tjocklek som är $$dx$$.

Det betyder att skalets volym, dvs volymselementet blir $dV=2\pi x\cdot ln(x)$ $dx$ .

Det är dessa volymer du nu ska integrera.

Du har fått fram rätt integrationsgränser, nämligen den inre radien $x_1=1$ och den yttre radien $x_2=e$ .

Totalvolymen blir alltså $V = \int_{1}^{e} d V = \int_{1}^{e} 2 π x \cdot \ln (x) d x$ .

Vill du beräkna den integralen eller pröva skivmetoden istället?

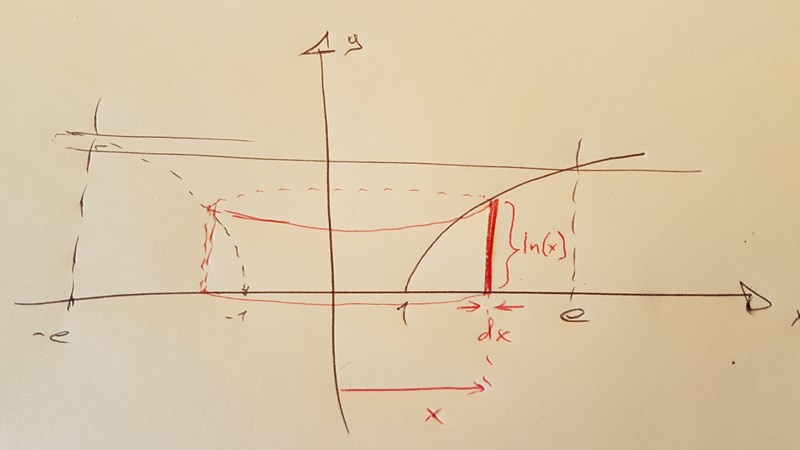
Så här bör din figur se ut ungefär om du vill använda skalmetoden:

Yngve skrev:
lamayo skrev:
Tack , känns som det klarnade lite. pi*r^2 dy är volymselemtet?
$π \int_{1}^{e} (lnx)^2 dy$ får följande om jag använder skivmetoden? lnx motsvarar väll funktionen f(x)?
Det är när du kommer hit som det är så ofantligt viktigt att du har ritat en figur och att du förstår hur rotationskroppen ser ut. Du blandar ihop det hela lite grann vilket tyder på att du inte har ritat din figur helt klart. Se förslag längst ner.
---------------------------
Om du använder skalmetoden: Rotationen sker kring y-axeln. Se framför dig (eller försök rita) ett cylindriskt skal runt y-axeln på avståndet $r$ (dvs $$x$) från y-axeln. Detta skal har en omkrets som är $$2\pi r $, dvs$ 2\pi x$$, en höjd $$h$$ som är $$ln(x)$$ och en tjocklek som är $$dx$$.
Det betyder att skalets volym, dvs volymselementet blir $dV=2\pi x\cdot ln(x)$ $dx$ .
Det är dessa volymer du nu ska integrera.
Du har fått fram rätt integrationsgränser, nämligen den inre radien $x_1=1$ och den yttre radien $x_2=e$ .
Totalvolymen blir alltså $V = \int_{1}^{e} d V = \int_{1}^{e} 2 π x \cdot \ln (x) d x$ .
Vill du beräkna den integralen eller pröva skivmetoden istället?
Så här bör din figur se ut ungefär om du vill använda skalmetoden:

hänger inte helt med, den ska väll nå ut till e eller?

Sedan ser jag inte varför omkretsen ska räknas ut på cylindern?

lamayo skrev:
Yngve skrev:

hänger inte helt med, den ska väll nå ut till e eller?
Sedan ser jag inte varför omkretsen ska räknas ut på cylindern?

Hela rotationsvolymen är uppdelad i ett stort antal cylindriska skal med väldigt liten tjocklek.

Det rödmarkerade föreställen ett av dessa cylindriska skal, på avstånd x från y-axeln.

Det cylindriska skalets area är omkretsen gånger höjden, dvs $A=2\pi r\cdot h$ och det cylindriska skalets volym är arean gånger tjockleken, dvs $dV=2\pi r\cdot h\cdot dr$ om tjockleken är $dr$ .

Eftersom rotationen är runt y-axeln så är $r=|x|$ och $dr=dx$ .

Eftersom höjden begränsas av funktionen $ln(x)$ så är $h=ln(x)$ .

Integrationen summerar volymsbidraget från alla dessa skal, från inre radien 1 till yttre radien e.

Yngve skrev:
lamayo skrev:
Yngve skrev:
hänger inte helt med, den ska väll nå ut till e eller?
Sedan ser jag inte varför omkretsen ska räknas ut på cylindern?
Hela rotationsvolymen är uppdelad i ett stort antal cylindriska skal med väldigt liten tjocklek.
Det rödmarkerade föreställen ett av dessa cylindriska skal, på avstånd x från y-axeln.
Det cylindriska skalets area är omkretsen gånger höjden, dvs $A=2\pi r\cdot h$ och det cylindriska skalets volym är arean gånger tjockleken, dvs $dV=2\pi r\cdot h\cdot dr$ om tjockleken är $dr$ .
Eftersom rotationen är runt y-axeln så är $r=|x|$ och $dr=dx$ .
Eftersom höjden begränsas av funktionen $ln(x)$ så är $h=ln(x)$ .
Integrationen summerar volymsbidraget från alla dessa skal, från inre radien 1 till yttre radien e.

aha , okej tror jag är med på det nu men som jag lärt mig är det bara sätta in allt i denna formel $π \int x^2 dy stämmer \det då inte ? eller motsvarar xlnxdx x^2 ?$

lamayo skrev:

aha , okej tror jag är med på det nu men som jag lärt mig är det bara sätta in allt i denna formel $π \int x^2 dy stämmer \det då inte ? eller motsvarar xlnxdx x^2 ?$

Att bara sätta in allt i en formel utan att veta vad man gör och varför är ett säkert recept för misslyckande.

Säg att du har en kofot hemma. Du vet att den är bra för att bräcka och bända, dra ur spikar och ta bort en massa saker. Så kommer jag och ber dig "ta bort" en sak som sitter fast. Skulle du då komma och försöka dra ut stickan i mitt finger med din kofot?

--------

Du blandar fortfarande ihop de olika metoderna. När du skriver $\pi x^2$ så handlar det om skivmetoden.

Läs mitt inlägg igen om skillnaden mellan de olika metoderna och fråga sedan här om de saker du inte förstår.

-----------

För att du ska ha en chans att kunna lösa uppgifter som handlar om rotationsvolymer så måste du förstå vad det är du gör och varför.

Börja med att titta på till exempel detta youtubeklipp som beskriver skalmetoden.

Det finns massor med klipp som beskriver både skalmetoden och skivmetoden (kallas ibland diskmetoden) på youtube.

Skriv tillbaka här dina frågor om det du inte förstår.

Yngve skrev:
lamayo skrev:
aha , okej tror jag är med på det nu men som jag lärt mig är det bara sätta in allt i denna formel $π \int x^2 dy stämmer \det då inte ? eller motsvarar xlnxdx x^2 ?$
Att bara sätta in allt i en formel utan att veta vad man gör och varför är ett säkert recept för misslyckande.
Säg att du har en kofot hemma. Du vet att den är bra för att bräcka och bända, dra ur spikar och ta bort en massa saker. Så kommer jag och ber dig "ta bort" en sak som sitter fast. Skulle du då komma och försöka dra ut stickan i mitt finger med din kofot?
--------
Du blandar fortfarande ihop de olika metoderna. När du skriver $\pi x^2$ så handlar det om skivmetoden.
Läs mitt inlägg igen om skillnaden mellan de olika metoderna och fråga sedan här om de saker du inte förstår.
-----------
För att du ska ha en chans att kunna lösa uppgifter som handlar om rotationsvolymer så måste du förstå vad det är du gör och varför.
Börja med att titta på till exempel detta youtubeklipp som beskriver skalmetoden.
Det finns massor med klipp som beskriver både skalmetoden och skivmetoden (kallas ibland diskmetoden) på youtube.
Skriv tillbaka här dina frågor om det du inte förstår.

kollat på viedon nu. Känns som jag förstår bättre. Ska kolla på några till. Nu har jag gjort det här:

Så det jag ska göra är att 1. Bestämma integrationsgränserna. 2. Skiva i x-led eller skala i y-led (testa vad som är lättast). 3. Räkna ut dV. 4. Sätta in det jag vet. 5. Integrera?

I punkt 3 i din figur skriver du skivmetoden och din figur antyder skivmetoden genom att den visar horisontella skivor på olika "höjd" (på olika avstånd från x-axeln).

Men integralen i punkt 4 tyder på att du använder skalmetoden.

Förstår du verkligen skillnaden mellan dem?

Om inte - fråga!

Yngve skrev:
I punkt 3 i din figur skriver du skivmetoden och din figur antyder skivmetoden genom att den visar horisontella skivor på olika "höjd" (på olika avstånd från x-axeln).
Men integralen i punkt 4 tyder på att du använder skalmetoden.
Förstår du verkligen skillnaden mellan dem?
Om inte - fråga!

Jag gör nog inte det. Förstårsättet de delas upp på men när det kommer till det som ska integreras i integralen mellan gränserna hänger jag inte med på. Tyckte jag förstod när jag kollat på olika videor och förklaringar men det lossnar liksom inte.

lamayo skrev:

Jag gör nog inte det. Förstårsättet de delas upp på men när det kommer till det som ska integreras i integralen mellan gränserna hänger jag inte med på. Tyckte jag förstod när jag kollat på olika videor och förklaringar men det lossnar liksom inte.

Om du använder skalmetoten:

Dela upp rotationsvolymen i cylindriska skal.

Ett skal på avståndet $r=x$ från y-axeln har omkretsen $2\pi r=2\pi x$ , höjden $ln(x)$ och alltså arean $A=2\pi x\cdot ln(x)$ .

Eftersom tjockleken är $dx$ så blir detta skals bidrag till totalvolymen $dV=2\pi x\cdot ln(x)\cdot dx$ .

Totalvolymen blir alltså integralen av $2\pi x\cdot ln(x)\cdot dx$ från $x=1$ till $x=e$ .

------

Om du använder skivmetoten:

Dela upp rotationsvolymen i cirkulära skivor. Varje skiva har ett hål i mitten. Inre radien är $x$ och yttre radien är $e$ .

En skiva på avståndet $y=ln(x)$ från x-axeln har en inre radie $r_1=x$ och en yttre radie $r_2=e$ . Varje skivas area är alltså $\pi (r_2)^2-\pi (r_1)^2=\pi e^2-\pi x^2=\pi (e^2-x^2)$ .

Eftersom $y=ln(x)$ så är $x=e^y$ och då är arean $\pi (e^2-(e^y)^2)=\pi (e^2-e^{2y})$ .

Eftersom tjockleken är $dy$ så blir denna skivas bidrag till totalvolymen $dV=\pi (e^2-e^{2y})\cdot dy$ .

Totalvolymen blir alltså integralen av $\pi (e^2-e^{2y})\cdot dy$ från $y=0$ till $y = l n (e)$ .

Yngve skrev:
lamayo skrev:
Jag gör nog inte det. Förstårsättet de delas upp på men när det kommer till det som ska integreras i integralen mellan gränserna hänger jag inte med på. Tyckte jag förstod när jag kollat på olika videor och förklaringar men det lossnar liksom inte.
Om du använder skalmetoten:
Dela upp rotationsvolymen i cylindriska skal.
Ett skal på avståndet $r=x$ från y-axeln har omkretsen $2\pi r=2\pi x$ , höjden $ln(x)$ och alltså arean $A=2\pi x\cdot ln(x)$ .
Eftersom tjockleken är $dx$ så blir detta skals bidrag till totalvolymen $dV=2\pi x\cdot ln(x)\cdot dx$ .
Totalvolymen blir alltså integralen av $2\pi x\cdot ln(x)\cdot dx$ från $x=1$ till $x=e$ .
------
Om du använder skivmetoten:
Dela upp rotationsvolymen i cirkulära skivor. Varje skiva har ett hål i mitten. Inre radien är $x$ och yttre radien är $e$ .
En skiva på avståndet $y=ln(x)$ från x-axeln har en inre radie $r_1=x$ och en yttre radie $r_2=e$ . Varje skivas area är alltså $\pi (r_2)^2-\pi (r_1)^2=\pi e^2-\pi x^2=\pi (e^2-x^2)$ .
Eftersom $y=ln(x)$ så är $x=e^y$ och då är arean $\pi (e^2-(e^y)^2)=\pi (e^2-e^{2y})$ .
Eftersom tjockleken är $dy$ så blir denna skivas bidrag till totalvolymen $dV=\pi (e^2-e^{2y})\cdot dy$ .
Totalvolymen blir alltså integralen av $\pi (e^2-e^{2y})\cdot dy$ från $y=0$ till $y = l n (e)$ .

tack för hjälpen! förstå skillnaden nu men behöver nog öva lite.