Rotationsvolym som i värsta stunder av matte 4
Jepp, nu är det 2018 och vi är tillbaka dit.
Yngve om du läser det, jag har undanträngt allt om rotationsvolym p.g.a trauman den orsakade hos mig.
Men det ser ut som det kommer på prov:
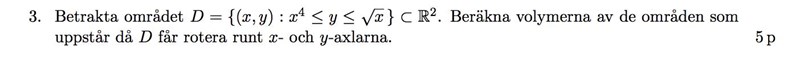 Rotationkring x-axeln, med figur i handen, ser jag som den volym mellan kurvan och , mellan noll och ett, med formeln .
Rotationkring x-axeln, med figur i handen, ser jag som den volym mellan kurvan och , mellan noll och ett, med formeln .
Men rotation kring y-då?
Det är ju samma figur, fast nu roterar vi horizontellt...??
(Snälla sig mig inte att senare i matematik kommer rotation moturs eller medurs kring y, x eller z axeln)
Ja, i stort sett kommer de båda rotationsfigurerna att se likadana ut, och om de båda funktionerna hade varit och (eller och ) så hade rotationskropparna varit lika, oberoende vilken av axlarna man roterar runt. Men nu kommer du att ha olika över- och underfunktioner i de båda fallen, så volymerna kommer att bli olika.
dajamanté skrev:Jepp, nu är det 2018 och vi är tillbaka dit.
Yngve om du läser det, jag har undanträngt allt om rotationsvolym p.g.a trauman den orsakade hos mig.
Men det ser ut som det kommer på prov:
Rotationkring x-axeln, med figur i handen, ser jag som den volym mellan kurvan och , mellan noll och ett, med formeln .
Men rotation kring y-då?
Det är ju samma figur, fast nu roterar vi horizontellt...??
(Snälla sig mig inte att senare i matematik kommer rotation moturs eller medurs kring y, x eller z axeln)
EDIT - stryker skämtet, ska nog inte skoja om såna saker 😀
Haha. Typ så här: Vid rotation medurs uppkommer en positiv rotationsvolym, men vid rotation moturs blir rotationsvolymen negativ 😁
Nejdå, var inte orolig Daja. Det är ingen skillnad.
Jag ber om ursäkt om jag traumatiserade dig med rotationsvolymer, men det är inte speciellt svårt om du bara ritar figurer och förstår hur volymerna ser ut.
Din beskrivning av område och integrationsgränser är rätt men din integral stämmer inte.
Om du använder skivmetoden så kommer varje skiva att ha ett hål i mitten som du måste ta hänsyn till. Varje skiva har alltså en inre och en yttre radie.
Rita in skivorna i genomskärning i koordinatsystemet så ser du nog hur det hänger ihop.
Vid rotation kring x-axeln är integrationsriktningen i x-led. Vid rotation runt y-axeln är integtationsriktningen i y-led.
Om du använder skalmetoden så blir det annorlunda.
Det är mest HON ( ) som traumatiserade mig så ingen fara Yngve 😁:
) som traumatiserade mig så ingen fara Yngve 😁:
oooooh jag tror att jag fattar.
En rotation... kan observeras... bara uppåt från neråt. Det finns inga rotation höger och vänster.
Därför blir b....
i led, men i y led måste vi tilta på huvudet och det blir tvärtom?
För mig var det samma system, fast roterande up och ner kring x-axel, och höger-vänster kring y-axel... Men en sånt rotation inte finns va?
(skalmetoden har jag totalt undergrävt)
Smaragdalena skrev:Ja, i stort sett kommer de båda rotationsfigurerna att se likadana ut, och om de båda funktionerna hade varit och (eller och ) så hade rotationskropparna varit lika, oberoende vilken av axlarna man roterar runt. Men nu kommer du att ha olika över- och underfunktioner i de båda fallen, så volymerna kommer att bli olika.
... what? why??
dajamanté skrev:Smaragdalena skrev:Ja, i stort sett kommer de båda rotationsfigurerna att se likadana ut, och om de båda funktionerna hade varit och (eller och ) så hade rotationskropparna varit lika, oberoende vilken av axlarna man roterar runt. Men nu kommer du att ha olika över- och underfunktioner i de båda fallen, så volymerna kommer att bli olika.
... what? why??
Standardfråga 1a: Har du ritat?
dajamanté skrev:Det är mest HON (
) som traumatiserade mig så ingen fara Yngve 😁:
oooooh jag tror att jag fattar.
En rotation... kan observeras... bara uppåt från neråt. Det finns inga rotation höger och vänster.
Därför blir b....
Ja det stämmer.
i led, men i y led måste vi tilta på huvudet och det blir tvärtom?
Vid rotation runt y-axeln ligger dina skivor staplade på varandra på x-axeln. Du ska då integrera i y-led från y = 0 till y = 1.
Du får då uttrycka skivornas inre och yttre radie som funktioner av y istället för x.
För mig var det samma system, fast roterande up och ner kring x-axel, och höger-vänster kring y-axel... Men en sånt rotation inte finns va?
Jag förstår nog inte riktigt detta ...
Jag menade, att jag trodde detta, eftersom det är samma plupp som roterar:
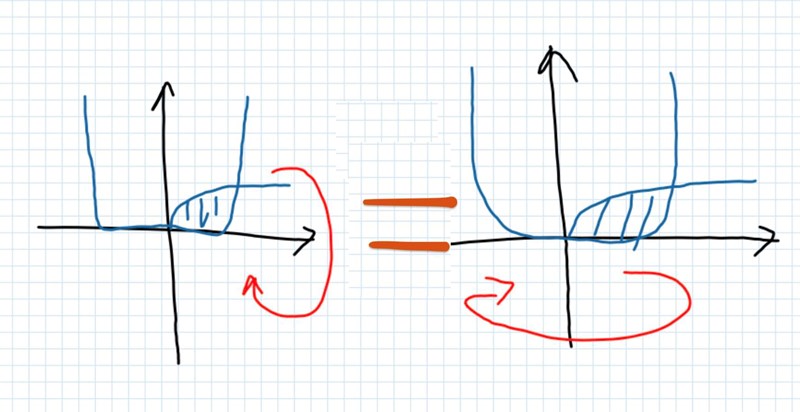
Men det är :
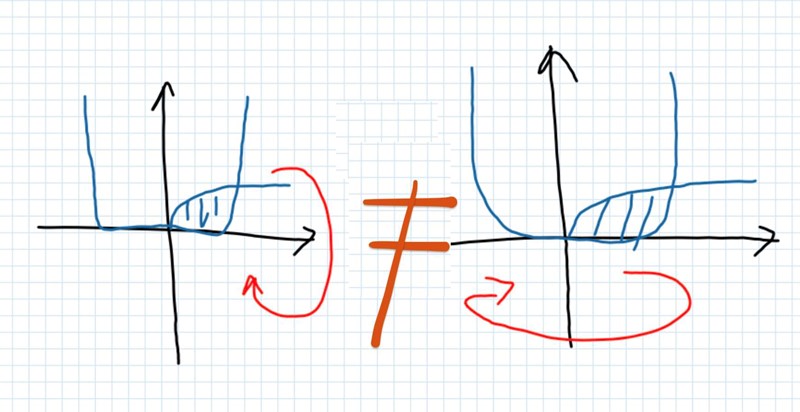
Utan man måste tänka:

Snälla Daja, rita alltid x-axeln åt höger och y-axeln uppåt, jag förstår inte alls vad du vill säga med dina skisser!
I båda fallen här får du en stapel med en massa skivor. Stapeln har höjden 1. Varje cylinderformad skiva har ett runt hål i mitten.
Om du roterar kring x-axeln så kommer ytterdiametern att vara och diametern på hålet (innerdiametern) att vara $$x^4. Integrera m a p x från 0 till 1.
Om du roterar kring y-axeln så kommer ytterdiametern att vara och innerdiametern är . Integrera m a p y från 0 till 1.
Smaragdalena skrev:Snälla Daja, rita alltid x-axeln åt höger och y-axeln uppåt, jag förstår inte alls vad du vill säga med dina skisser!
Jag den är ful, men jag menade att om vi roterar hela grafen då förstår man varför yttre och inre funktion byter plats.
I båda fallen här får du en stapel med en massa skivor. Stapeln har höjden 1. Varje cylinderformad skiva har ett runt hål i mitten.
Om du roterar kring x-axeln så kommer ytterdiametern att vara och diametern på hålet (innerdiametern) att vara $$x^4. Integrera m a p x från 0 till 1.
Ja, kanske det...
Om du roterar kring y-axeln så kommer ytterdiametern att vara och innerdiametern är . Integrera m a p y från 0 till 1.
Nu har jag skissat och sätt på pilar... men är det inte negativa och ?
dajamanté skrev:Smaragdalena skrev:Snälla Daja, rita alltid x-axeln åt höger och y-axeln uppåt, jag förstår inte alls vad du vill säga med dina skisser!
Jag den är ful, men jag menade att om vi roterar hela grafen då förstår man varför yttre och inre funktion byter plats.
Jag skulle rita så här för att förstå det hela själv. Skivorna i genomskärning i rött.

Rotation runt x-axeln: Skivorna har x-axeln som centrum och de "står" bredvid varandra från x = 0 (y-axeln) till x = 1. För varje värde på x så fås inre och yttre radie av sambanden respektive .
Rotation runt y-axeln: Skivorna har y-axeln som centrum och de "ligger" staplade på varandra från y = 0 (x-axeln) till y = 1. För varje värde på y så fås inre och yttre radie av sambanden respektive , dvs respektive .
Där ser man skillnaden mellan en riktigt mathemagician och nåt amatör. Ska rita ner den här på anteckningsblock.
Tack Yngve o Smaragdalena!
dajamanté skrev:Där ser man skillnaden mellan en riktigt mathemagician och nåt amatör. Ska rita ner den här på anteckningsblock.
Tack Yngve o Smaragdalena!
Tack, men det är betydligt mer träning än magi, Daja.
Det är oftast vad gör skillnaden :)




