19 svar

397 visningar

dajamanté behöver inte mer hjälp

Rotationsvolymer: alltid roligt tills det är inte det längre 1

Som rubriken säger, jag tyckte att det var roligt tills det blev mystifierande helt plötsligt:

Låt det område som begränsas av kurvan y=ln(x), linjen x = e samt x-axeln rotera kring y-axeln. Bestäm volymen av den uppkomma rotationskroppen.

(Nej låt den inte tänkte jag...) Men iaf, jag kunde inte lösa det men faciten och gamla tråd på forumet säger att man måste räkna volymen på cylinder med radie e som roterar kring y-axeln och substrahera området på vänster sidan av y=ln(x)

Så om y=lnx och vi behöver x^2 i radien får vi $e^{2 y} = x^{2}$

Men jag förstår inte varför arean om vänster av den gröna kurvan blir också:

$\int_{0}^{1} e^{2 y} d y$ ?

Om vänster av gröna kurvan är det area över grafen (wrt till den gröna kurvan!), eller? Om man kollar från perspektiven av arean som begränsas av x-axeln, y-axeln, gröna och oranga kurva den ser ut mer som arean under en sorts y= $e^{- x}$ kurva?

Jag förstår inte vad det är du inte förstår, kan du förtydliga det?

Det stämmer att det enklaste sättet att beräkna rotationskroppens volym är att först beräkna cylindervolymen och sedan subtrahera volymen av rotationskroppen som uppstår då området till vänster om kurvan y = ln(x) roterar kring y-axeln.

Visa dina uträkningar, steg för steg enligt min checklista.

Jag får svaret om jag följer faciten, vad jag är inte med (verkligen inte) är att, vi måste väl substrahera area under kurva. y=ln(x) är den gröna kurva. Men arean under kurvan är inte arean som kommer att substraheras!

Gör som Yngve föreslog och visa dina utrräkningar steg för steg. Vi som skriver här på Pluggakuten är bra på matte, men ganska usla på tankeläsning.

Daja skrev :
Jag får svaret om jag följer faciten, vad jag är inte med (verkligen inte) är att, vi måste väl substrahera area under kurva. y=ln(x) är den gröna kurva. Men arean under kurvan är inte arean som kommer att substraheras!

Varför vill du subtrahera arean under kurvan?

Eftersom du pratar om att subtrahera arean under kurvan så verkar det som om du tänker att området roterar kring x-axeln?

Har du verkligen ritat en figur och gått klart för dig hur området som roterar ser ut och hur rotationskroppen kommer att se ut (de första punkterna i checklistan)?

Kan du visa din figur eller beskriva med ord hur rotationskroppen ser ut?

Om jag måste citera EN sak som jag har lärt från dig, det är väl att rita figur! (Jag bifogar en av många chef d'oeuvres)

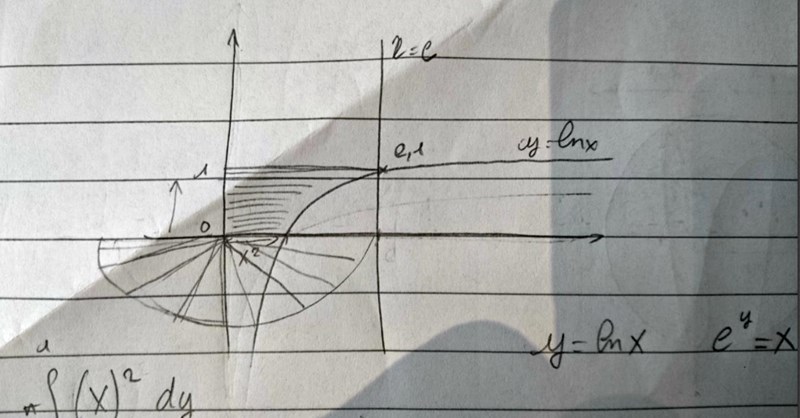
Batongerna representerar cylinder med radie e.

Kroppen som måste tas bort är väl den randiga (mellan den gröna och oranga på desmos)?

Daja skrev :
Om jag måste citera EN sak som jag har lärt från dig, det är väl att rita figur! (Jag bifogar en av många chef d'oeuvres)
Batongerna representerar cylinder med radie e.
Kroppen som måste tas bort är väl den randiga (mellan den gröna och oranga på desmos)?

Snygg figur!

Ja det stämmer. Men varför säger du då att du vill subtrahera arean under kurvan?

Kortfattat och slarvigt uttryckt:

Sökt volym är "cylindervolym (blå linje)" - "volym ovanför kurvan (mellan grön och orange)".

Så du ska inte alls subtrahera volymen under kurvan. Tvärtom, det är ju den du ska räkna ut!

smaragdalena skrev :
Gör som Yngve föreslog och visa dina utrräkningar steg för steg. Vi som skriver här på Pluggakuten är bra på matte, men ganska usla på tankeläsning.

Jag tycker att det är även lite scary hur bra på matte ni alla är :)

Grejen är att jag hittar lösning när jag följer faciten men jag är inte med resonnemang :/

Så här blev det:

$π \int_{0}^{1} x^{2} dy$

$y = \ln (x) \to e^{y} = x \to e^{2 y} = x^{2}$

$π \int_{0}^{1} e^{2 y} dy \to π {[\frac{e^{2 y}}{2}]}_{0}^{1} \to π {[\frac{e^{2} - e^{0}}{2}]}_{0}^{1} \to π (\frac{e^{2} - 1}{2})$

Cylinder som substraheras har basen ${πe}^{2}$ och höjden 1.

$\frac{2 {πe}^{2}}{2} - π (\frac{e^{2} - 1}{2}) = \frac{π (e^{2} + 1)}{2}$

Yngve skrev :
Kortfattat och slarvigt uttryckt:
Sökt volym är "cylindervolym (blå linje)" - "volym ovanför kurvan (mellan grön och orange)".
Så du ska inte alls subtrahera volymen under kurvan. Tvärtom, det är ju den du ska räkna ut!

Precis, därför förstår jag inte när faciten ger ledtråden:

"Den sökta volymen kan beräknas som skillnaden i volym mellan en cylinder och en rotationsvolym som bildas när kurvan roterar kring y-axeln."

Med det, dom mennar väl den randiga arean på min figur (och mellan x-axel, y-axeln, samt gröna och oranga linjer på desmos?) som ligger inte under y=ln(x)?

EDIT: nu har jag läst om, jag är inte säkert om vilket är sökt volym längre!

eller

Det är det gula området som skall rotera runt y-axeln. Det står ju i uppgiften att en av begränsningslinjerna skall vara x = e.

Ok, så isf måste jag subtrahera den randiga area. Som ligger inte under y=lnx!

Om jag skulle lösa den här uppgiften skulle jag se det som en samling tunna skikvor, formade som ringar. Alla ringarna har ytterdiameten 2 och innerdiametern $e^y$ . Arean av en skiva blir alltså $\pi (2^2 - e^{2y})$ , tjockleken av varje skiva är dx. Volymen av varje skiva (ring) blir arean gånger tjockleken, och så integrerar man det från y = 0 till y = 1. Detta är skivmetoden.

Man kan också lösa den med skalmetoden: Då ser man det som en samling tunna ringar inuti varandra, som en lök ungefär, eller en rulle toapapper (fast den är egentligen en spiral, inte an massa separata skal - det vore opraktiskt annars!). Varje skal är en cirkel med radien x, så omkretsen blir $2 \pi x$ ,och med höjden ln x. Varje skal får volymen omkretsen gånger höjden, och så får man integrera från x = 1 till x = e.

Ringarna i det första fallet är alltså sådana som man får om man ritar en cirkel inuti en cirkel och klipper ut den, och i det andra fallet som om man klistrar ihop en rektangel till en ring.

Daja skrev :
Ok, så isf måste jag subtrahera den randiga area. Som ligger inte under y=lnx!

Ja det stämmer. Men jag håller med om att det inte i facit klart och tydligt framgår vilken volym som skulle subtraheras.

smaragdalena skrev :
Om jag skulle lösa den här uppgiften skulle jag se det som en samling tunna skikvor, formade som ringar. Alla ringarna har ytterdiameten 2 och innerdiametern $e^y$ . Arean av en skiva blir alltså $\pi (2^2 - e^{2y})$ , tjockleken av varje skiva är dx. Volymen av varje skiva (ring) blir arean gånger tjockleken, och så integrerar man det från y = 0 till y = 1. Detta är skivmetoden.
Man kan också lösa den med skalmetoden: Då ser man det som en samling tunna ringar inuti varandra, som en lök ungefär, eller en rulle toapapper (fast den är egentligen en spiral, inte an massa separata skal - det vore opraktiskt annars!). Varje skal är en cirkel med radien x, så omkretsen blir $2 \pi x$ ,och med höjden ln x. Varje skal får volymen omkretsen gånger höjden, och så får man integrera från x = 1 till x = e.
Ringarna i det första fallet är alltså sådana som man får om man ritar en cirkel inuti en cirkel och klipper ut den, och i det andra fallet som om man klistrar ihop en rektangel till en ring.

Jag har jättesvårt att visualisera -men ok, ytter och innerdiameter, som för en ring!

Jag har tagit skivmetoden och råkat (igen) få något helt tokigt. Du säger att "Alla ringarna har ytterdiameten 2 och innerdiametern $e^y$ .", så vi pratar nog om volymen som måste försvinna?

$\int_{0}^{1} π (2^{2} - e^{2 y}) = π [(4 * 1 - \frac{e^{2}}{2}) - (4 * 0 - \frac{e^{2 * 0}}{2})] = (3, 5 π - \frac{{πe}^{2}}{2})$ ?

Med löken som jag har också svårt att visualisera, fast det gick bra igår... en vanfråga antar jag.. Men:

$\int_{0}^{1} 2 π x * \ln x d x$

Hur integrerar man lnx?

utan att ha kollat dina beräkningar i övrigt: Integralen löser du med partiell integration.

(För övrigt har ln(x) den primitiva funktionen xln(x)-x, men det behöver man inte kunna utan det slår man upp i formelsamlingen. vill man härleda det så integrerar man 1*ln(x) med partiell integration )

Volymen som behöver försvinna i Yngves metod är hålet i mitten av ringarna.

Den primitiva funktionen till log x är x(log(x)-1) + C, och primitiv funktion till x(log x) är $\frac{1}{4} x^{2} (2 \log x - 1)$ + konstant, men i det här fallet väljer man nog skivmetoden!

PS. Jag kan inte allt utantill - WolframAlpha kan (nästan) allt!

smaragdalena skrev :
Volymen som behöver försvinna i Yngves metod är hålet i mitten av ringarna.

Jo, och det är det som jag tyckte var tråkigt i den här uppgiften, för hållet skapades övanpå lnx kurva, så jag förståd inte hur jag kunde integrera den.

Det finns ofta flera sätt att beräkna rotationsvolymer.

I detta exempel har vi pratat om tre olika sätt.

Skivmetoden 1 "Yngves metod" (skivor utan hål i mitten): Räkna ut cylinderns volym och subtrahera sedan den volym som uppstår när området ovanför kurvan roterar kring y-axeln (integrera fram den)
Skivmetoden 2 "Smaragdalenas metod 1" (skivor med hål i mitten): Integrera fram den efterfrågade volymen direkt (den volym som uppstår när området under kurvan roterar kring y-axeln).
Skalmetoden "Smaragdalenas metod 2": Räkna ut volymen direkt genom att dela upp rotationsvolymen i cylindriska skal kring y-axeln och integrera från r = 1 till r = e.

Det blir lätt lite förvirrat när vi har så många metoder igång samtidigt och det inte är självklart vilken metod som frågor och svar avser.

Tack för att du sammanfattar.

Jo, det känns lite:

Jag ska sätta en stjärna på tråden för att göra en latthund... men senare :D

Svara

Visa senaste svar