Rotera runt y-axeln

Hej!

Jag har denna uppgift:

Ett område bestäms av y-axeln, funktionen y = och linjen y = 4. Beräkna volymen av den rotationskropp som uppstår då området tillåts rotera runt y-axeln.

Graf:

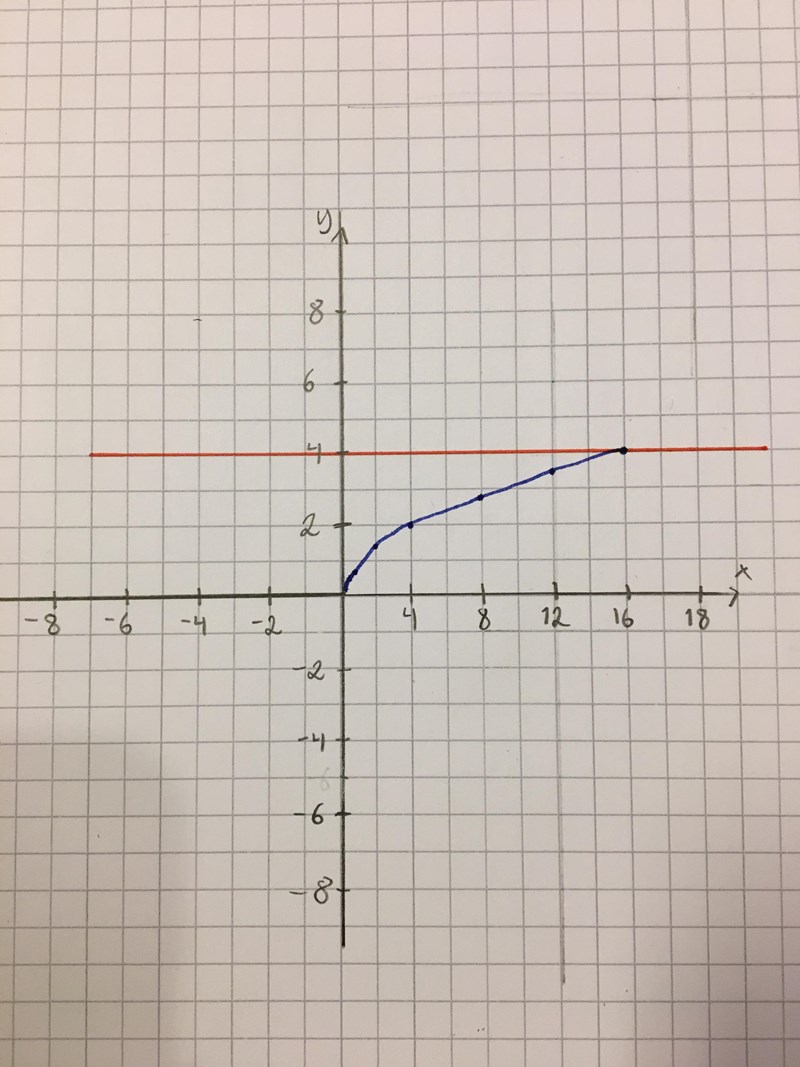
Så integrationsgränserna är 0 till 4

$y = \sqrt{x} y^{2} = (\sqrt{x})^{2} y^{2} = x$

Jag har haft något jätte problem att förstå detta idag, jag vet redan att den primitiva funktionen ska vara $π {[\frac{x^{5}}{5}]}_{0}^{4}$ ja eller det blir väl $π {[\frac{y^{5}}{5}]}^{4}_{0}$ men jag förstår verkligen inte hur det kan bli det? Isf måste jag redan ha fått till funktionen $π (x^{4})$ vilket jag inte har. Någon som vill förklara? :)

Här är ett jätte bra exempel från boken:

Alltså på hur de får $\sqrt{x} t i l l π [\frac{y^{5}}{5}]$

Jag ser verkligen inte hur reglerna funkar.

De använder skivmetoden med x som radie. Har du inte gjort sådana problem redan?

Funktionen är $f(x)=\sqrt{x}$ . Du kan tänka dig rotationskroppen som en massa platta skivor med sina centrum längs med y-axeln. Varje skiva har arean $\pi r^2$ , där $r = x = y^{2}$ . Är du med så långt?

Laguna skrev:
De använder skivmetoden med x som radie. Har du inte gjort sådana problem redan?

Jo, tror jag blandar ihop vad som ska höjas upp i 2 då man gör det för på y och x i denna uppgift. Jag tror jag förstår nu :)

Smaragdalena skrev:
Funktionen är $f(x)=\sqrt{x}$ . Du kan tänka dig rotationskroppen som en massa platta skivor med sina centrum längs med y-axeln. Varje skiva har arean $\pi r^2$ , där $r = x = y^{2}$ . Är du med så långt?

Japp då förstår jag:)

Jag har fått svart till $\frac{1024 π}{5} = 204.8 π$

Vet dock inte vilket jag bör svara med, står inget i uppgiften om att det ska vara ett exakt svar.

Svara Avbryt

Visa senaste svar