Roterande system och cylindriska koordinater
Hej
Detta är uppgiften:
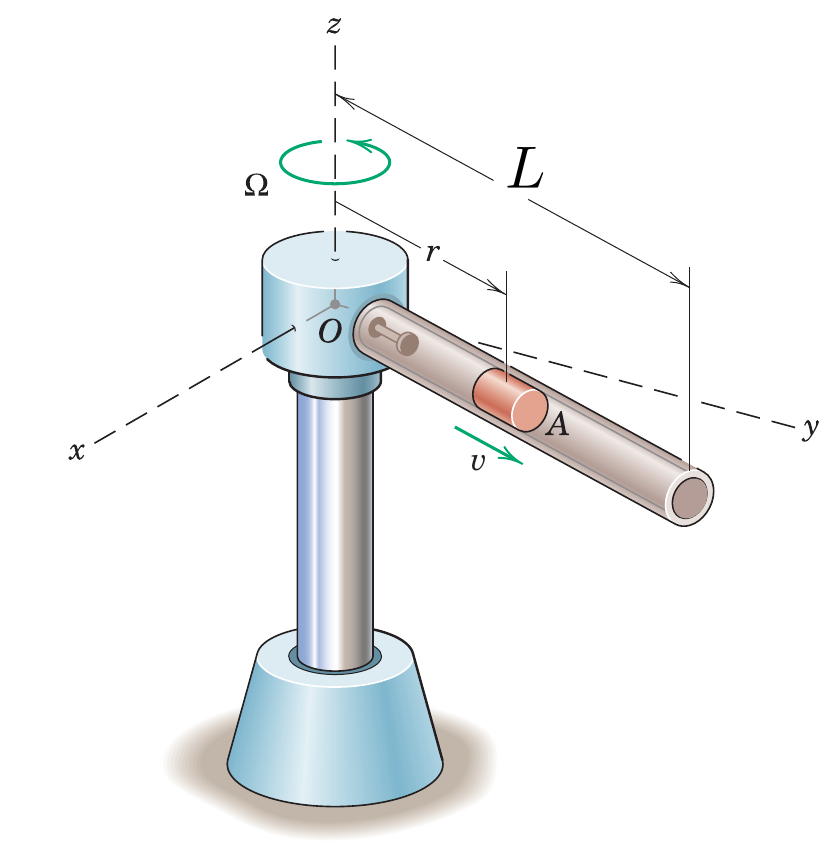
Det ihåliga röret med längden L roterar runt en vertikal axel genom O med en konstant vinkelhastiget . En cylinder med massa glider friktionsfritt inuti röret. Cylindern börjar på ett avstånd och har då farten v_0 längs röret. Beräkna magnituden av den horisontella kraften som verkar på cylindern precis när den lämnar röret. Svara i termer av och . [Notera att i figuren är det som kallas $\omega$ i uppgiftstexten.
Jag kan lösa hela uppgiften men bara om jag använder att accelerationen i -riktning är 0. Hur kommer man fram till att det gäller här? Om det gäller borde inte då också vara konstant, vilket den uppenbarligen inte är. Anar att det har med någon grundläggande förståelse jag missat.
Röret är friktionsfritt så ingen kraft påverkar i -riktningen. Fr = 0.
Newton säger att Fr = mar. Eftersom Fr är noll så måste vi ha att ar = 0.
0 = . Alltså kan inte vara noll.
Vad är det jag tänker fel här då? Kanske att jag likställer med ?
Ja, det är nog huvet på spiken.
Tänk att r är konstant, då rör du dig i en cirkel och får ändock en ar komponent som är skild från noll - det som ibland kallas centripetalacceleration.
Precis, och här gäller tvärtom. Accelerationen är nollskilt men pga centripetalaccelerationen blir den totala accelerationen i led 0.
Jag ska nog kunna se det framför mig men jag tycker det är lite väl random hur bidragen kommer in i accelerationen i polära koordinater.
Ja, det kan vara svårt att visualisera. Man får använda matematiken som en hjälpande hand i nöden.
Hur gör du för att komma ihåg? Sitter det bara eller kan du lätt härleda det i huvudet?
Till tentan har man säkert räknat så många tal att det sitter.
Men jag brukar göra en snabb härledning eftersom tentan var för länge sedan.
Det hjälper om man känner till formlerna
=
.



