Roterande volymer som var roliga men inte längre 3

Med asinx+ bcosx är lika med får vi att kurvan är lika med . http://sketchtoy.com/68241662 (lite ful men...)
Så kurvan startar vid , når med x=, noll igen vid och - vid .
Tror jag...
Så jag antar att jag kan integrera mellan och , och multiplicera med 2.
Saken roterar kring x-axeln, radien är därför y^2.
Nu måste vi inte glömma att gå tillbaka till den ursprungliga formeln, (hade provat integrera och blev halv galen :D)
= med triggettan och allt 2sinxcosx= sin2x
Nu integrerar vi:
blir . Alla cos termer försvinner... och det blir dvs HELT FEeeeeL. Orkar inte.
Jag förstår inte vad du har kommit fram till.
Din figur verkar inte ha med uppgiften att göra.
Dina integrationsgränser är inte korrekta.
Om du skissar y = sin(x) + cos(x) så ser den ut så här (det område som ska rotera runt x-axeln är gulmarkerat):
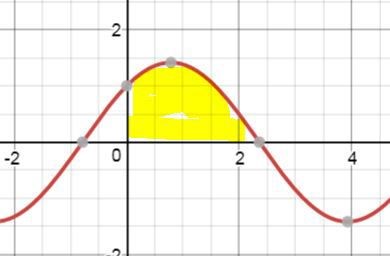
Yngve skrev :Jag förstår inte vad du har kommit fram till.
Din figur verkar inte ha med uppgiften att göra.
Dina integrationsgränser är inte korrekta.
Om du skissar y = sin(x) + cos(x) så ser den ut så här (det område som ska rotera runt x-axeln är gulmarkerat):
Hoppsan, den begränsas av dom positiva koordinat-axlarna X()!...
Och nu när jag räknar med integranden hittar jag rätt, .
Tack Yngve! (... men det finns mer icke roliga uppgifter på g...)



