Samband m. rötter & koefficient polynomekvation (Matematik/Matte 4/Komplexa tal)

Jag är lite osäker på vad de letar efter. Det jag kommer skriva nedan gäller för alla polynom, inte bara med rationella koefficienter (vilket gör mig lite osäker, men jag kan inte tänka ut något annat just nu som de kan vilja ha).

Det jag gissar att de vill ha är att koefficienten framför $x^{n-1}$ termen kommer alltid vara summan av rötterna till polynomekvationen med omvänt tecken (gånger -1).

Hur kommer man fram till detta? Jag ska sova, så jag vill inte skriva ut allt just nu, men kika på detta:

Enligt faktorsaten kan man skriva polynomet som

$(x-r_1)(x-r_2)\cdots(x-r_n)$

Där $r_k$ är den k:te roten till polynomet. Testa för små $n$ att multiplicera ut uttrycket, hur ser $x^{n-1}$ termen ut?

Jag tror nog som AkexMu, men kan du ladda upp en bild på uppgiften?

Exempel och bra träning:

Utgå från en andragradsekvation $x^2+px+q=0$ och dess rötter $x_1$ och $x_2$

Visa nu att följande samband gäller mellan rötterna och koefficienterna:

$p=-(x_1+x_2)$
$q=x_1\cdot x_2$

Det ser ut såhär:

Dkcre skrev:
Det ser ut såhär:

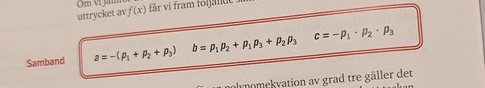Det frågan ställer är essentiellt en generalisering av detta samband för $a$ när man har högre gradtal än $3$ .

Yngve skrev:
Jag tror nog som AkexMu, men kan du ladda upp en bild på uppgiften?

Exempel och bra träning:

Utgå från en andragradsekvation $x^2+px+q=0$ och dess rötter $x_1$ och $x_2$

Visa nu att följande samband gäller mellan rötterna och koefficienterna:

$p=-(x_1+x_2)$

$q=x_1\cdot x_2$

Har jag visat något nu?

AlexMu skrev:
Dkcre skrev:
Det ser ut såhär:

Det frågan ställer är essentiellt en generalisering av detta samband för $a$ när man har högre gradtal än $3$ .

Ja, precis.

Dkcre skrev:
Yngve skrev:
Jag tror nog som AkexMu, men kan du ladda upp en bild på uppgiften?

Exempel och bra träning:

Utgå från en andragradsekvation $x^2+px+q=0$ och dess rötter $x_1$ och $x_2$

Visa nu att följande samband gäller mellan rötterna och koefficienterna:

$p=-(x_1+x_2)$

$q=x_1\cdot x_2$

Har jag visat något nu?

Ja. Det där är nästan rätt (litet fel på tecknet i $x$ -termen, efter att du bröt ut $x$ ). Kan du göra något likande för högre gradtal?

Nej jag tror inte det.

Här är något

Dkcre skrev:
Nej jag tror inte det.

Här är något

Ett knep som kan göra denna multiplikation lättare:
Du har redan beräknat $(x-p_1)(x-p_2)$ till $x^2 - x(p_1+p_2) + p_1 p_2$

Då vet du automatiskt att

$(x-p_1)(x-p_2)(x-p_3) = (x^2 - x(p_1 +p_2) + p_1p_2)(x-p_3)$

Kan du fortsätta härifrån?

Också, jag redigerade mitt inlägg rätt sent, såg du det var ett litet misstag i den förra multiplikationen?

Jag är ledsen, men jag förstår inte dina omskrivningar riktigt.

Ska jag kunna se något mönster i det här nu?

Tror inte jag klarar av att lösa det här, förstår nästan ingenting. Var mer nyfiken på hur man går tillväga bara.

Dkcre skrev:
Jag är ledsen, men jag förstår inte dina omskrivningar riktigt.

Ska jag kunna se något mönster i det här nu?

Nej, du ska inte se något mönster direkt.

Iden är att vi redan har beräknat vad

$(x-p_1)(x-p_2)$ är

När vi ska beräkna $(x-p_1)(x-p_2)(x-p_3)$ kan vi utnyttja det. Vi vet ju redan produkten av de första två faktorerna! Så vi kan bara substituera in det, det var mitt lilla "knep".

Jag tänkte att det är en lättare produkt än när vi har tre parenteser att multiplicera ihop.

Jaha okej, du hänger jag med i vad du gjorde.

Antar att jag multiplicerade fel i det jag gjorde då.

Dkcre skrev:
Antar att jag multiplicerade fel i det jag gjorde då.

Ja, något blev fel. Det är knepigt att multiplicera ihop tre eller flera parenteser "bara sådär". Därför rekommenderar jag att först multiplicera ihop de första två för sig, och sedan multiplicera ihop resultatet med den sista.

Det är nog en bra rekommendation men jag klarar inte det heller.

Kom fram till följande:

Ett sätt man kan tänka med lite substitution!

Vi vet redan att $(x-p_1)(x-p_2) = x^2 - x(p_1 + p_2) + p_1 p_2$ .

Men vi kan för enkelhetens skull låta

$(x-p_1)(x-p_2) = t$ .

Då har vi också att $t = x^2 - x(p_1 + p_2) + p_1 p_2$

Då är $(x-p_1)(x-p_2)(x-p_3) = t(x-p_3)$

Detta kan då multipliceras ut till

$xt - p_3t$

Nu substituerar vi in värdet på $t$ .

För den första termen: $xt = x(x^2 - x(p_1 + p_2) + p_1 p_2)$
För den andra termen: $p_3 t = p_3(x^2 - x(p_1 + p_2) + p_1 p_2)$

Kan du fortsätta härifrån?

Tack, det hjälper 😊

Är det rätt? Ska jag samla termer och strukturera uttrycket och då hitta något mönster?

Nästan!!

Tänk på att den andra termen hade ett minustecken framför sig. Detta minus ska ju hamna på allt innanför termen $p_3 t$ , inte bara det första!

Vi har egentligen då:

$xt - p_3 t = x(x^2 - x(p_1+p_2)+p_1p_2)-p_3(x^2 - x(p_1+p_2)+p_1p_2)$

Minustecknet måste distribueras!

Dkcre skrev:
Ska jag samla termer och strukturera uttrycket och då hitta något mönster?

Strukturera ut uttrycket baserat på $x^k$ -termerna. Hur ser strukturen ut i jämförelse med polynomet med gradtal 2? Då kanske du kan gissa hur gradtal 4 ser ut på ett ungefär, det viktiga är $x^{n-1}$ termen! (för denna fråga)

Suck okej.. jag försöker igen.

Vilken är x^n-1 termen? Menar vi x^2 i en tredjegradare då?

Dkcre skrev:
Vilken är x^n-1 termen? Menar vi x^2 i en tredjegradare då?

Ja precis.

Okej,

Får bli imorgonkväll, jag orkar inte mer..

Tack för hjälpen. Godnatt 😊

Dkcre skrev:
Okej,

Får bli imorgonkväll, jag orkar inte mer..

Tack för hjälpen. Godnatt 😊

Okej! Godnatt!

Är det rätt nudå?

Ni är duktiga som kan hålla koll på alla siffror, verkar ha någon koncentrationssvårighet för jag får ont i huvudet nästan direkt sen snurrar det bara.

Det verkar vara rätt. Fast det här har ju ingenting med formeln att göra..

Vet egentligen inte ens vad formel innebär, det är ju bara att multiplicera ihop alla faktorer och sen faktorera ut x eller hur man uttrycker det så har man ju sambandet.

Den enda som jag är osäker på hur den fortsätter är mönstret för bx. Är det p1p2, p1p3, p1p4 ända till p1pn, och sedan p2p3, p2p4 till p2pn etc eller något annat.

Japp! Det där stämmer! Jag är på mobil nu, men när jag kommer hem kan jag skriva ut hur man fortsätter för högre gradtal och vad resultatet blir.

Målet med detta är att hitta förhållandet mellan ett polynoms rötter och dess koefficienter. Förhållandet kallas för Viétes formler.

För ett generellt polynom med ledande koefficient 1 (Kolla länken om du vill se hur formlerna blir om man inte har ledande koefficient 1. Det spelar inte särskilt stor roll tycker jag. Man kan alltid dividera/multiplicera för att skala om polynomet till koefficient 1) låter vi den ha denna form:

$x^n + a_{n-1}x^{n-1} + a_{n-2}x^{n-2}+\dots + a_1 x + a_0$

Om rötterna är $p_1, p_2, \dots, p_n$ så gäller det att

$a_{n-1} = -(p_1 + p_2 + \dots +p_n)$
$a_{n-2} = (p_1p_2 + p_1 p_3 + \dots +p_{n-1}p_n)$
(varje rot paras ihop med alla andra, se exempel för $n=4$ nedan)
...
hela vägen ned till
$a_0 = (-1)^n(p_1p_2\cdots p_n)$

Rätt mycket att ta in! Vi kollar på ett exempel för ett fjärdegradspolynom:

$x^4 + ax^3 + bx^2 + cx + d$

Enligt formlerna gäller det att

$a = -(p_1 + p_2 + p_3 + p_4)$

$b = (p_1 p_2 + p_1p_3 + p_1p_4 + p_2p_3 + p_2p_4 + p_3p_4)$

$c = -(p_1p_2p_3 + p_1p_3p_4 + p_2p_3p_4)$

$d = p_1p_2p_3p_4$

Den ursprungliga uppgiften var ju att visa hur $x^{n-1}$ -termens koefficient förhåller sig till rötterna, vilket då är $-(p_1+p_2+\dots +p_n)$ enligt Viétes formler från tidigare.

Hur kan vi visa detta?

Vi kan göra det lite rekursivt som var en del av mitt "knep" från tidigare. Vi kan utnyttja resultatet för polynomet av gradtal $n-1$ för att få reda på vad som händer för gradtal $n$ .

En annan sak vi kan utnyttja är att vi bara ska visa vad som händer för $x^{n-1}$ termen. Vad som händer för de andra $x^k$ -termerna spelar ingen roll!

Exempel för $n=4$

Vi vill hitta $x^{n-1} = x^3$ -termen i polynomet

$(x-p_1)(x-p_2)(x-p_3)(x-p_4)$

Du har redan räknat ut vad $(x-p_1)(x-p_2)(x-p_3)$ så vi kan substituera in det! Produkten ovan är alltså lika med:

$(x^3 - x^2(p_1+p_2+p_3)+x(p_1p_2 + p_1p_3 + p_2p_3) - p_1p_2p_3)(x-p_4)$

MEN, vi bryr oss bara om vad $x^3$ termen i produkten är. De flesta termerna när vi utför denna produkt kommer inte ha en faktor av $x^3$ . Nedan har jag färgat de två produkterna som ger en $x^3$ faktor, resten spelar ingen som helst roll i vår produkt (de i motsvarande färg ska multipliceras).

$($ $\color{red}x^3$ $\color{blue}- x^2(p_1+p_2+p_3)$ $+x(p_1p_2 + p_1p_3 + p_2p_3) - p_1p_2p_3)($ $\color{blue}x$ $\color{red}-$ $\color{red}p_4$ $)$

Om vi utför dessa multiplikationer får vi

$- x^2(p_1+p_2+p_3)\cdot x +x^3 \cdot (-p_4)= -x^3(p_1+p_2+p_3) - x^3p_4$

Vi kan bryta ut $-x^3$ vilket get oss

$-x^3(p_1+p_2+p_3+p_4) = x^3 \cdot -(p_1+p_2+p_3+p_4)$

Vilket är exakt det som beskrivs av Viétes formler!

Det här kan man fortsätta eller bevisa generellt med hjälp av induktion. Har du lärt dig induktion?

Dessa formler är rätt kraftfulla. Om vi har polynomet

$x^3-2x^2 + 4x + 1$

Vi vet inget om rötterna, men automatiskt har vi förhållandena

$p_1 + p_2 + p_3 = 2$
$p_1p_2 + p_1p_3 + p_2p_3 = 4$
$p_1p_2p_3 = -1$

Detta kan vara rätt kraftfullt för att lösa vissa uppgifter. Ett roligt exempel är denna:
Denna fråga låter rätt bisarr, och det är den, men om man vill beräkna exempelvis arean behöver vi inte beräkna rötterna. Vi kan bara utnyttja Viétes formler! (och några triangelformler)

Vi vet exempelvis automatiskt omkretsen: Det är summan av sidlängderna, alltså summan av alla rötterna till polynomet. Då kan vi använda Viétes formler för att dra slutsatsen att det är koefficienten framför $x^2$ -termen med omvänt tecken! Eller då: Omkretsen i triangeln är $6+2\sqrt 2$ . Arean är lite knepigare att få fram, men det är fullt möjligt utan att finna rötterna.

Nej, har inte lärt mig induktion. Men jag grejar inte det där i alla fall, jag får ont i huvudet. Det här var något av ett extra avsnitt i boken på 4 uppgifter, måste hoppa till derivata och integraler innan jag håller på med något annat. Hoppade över det för att köra komplexa tal som känns roligare.

Men tack för hjälpen! Och jag kan se hur det kan vara användbart.

Vad menar du med x^k där?

Dkcre skrev:
Vad menar du med x^k där?

Bara att det vara någon annan exponent. I argumentet brydde vi oss bara om $x^{n-1}$ -termen. Alla andra termer struntar vi i

Okej