Samband mellan Kon och cylinder?
Frågan lyder:
En cylinder gröps ur med en kon. Konen har samma höjd som cylinderns diameter. Cylindern är dubbelt så hög som konen.
visa att den urgröpta cylinderns volym är:
10 x pi x r^3 / 3
Jag förstår inte hur man bör tänka, jag har skrivit dock formeln för både cylindern och konen men kommer ingen vart.
tacksam för seriösa svar.
Börja med att rita en figur. Det kommer att underlätta för dig.
yes, har bilden här, har även ritat både konen och cylinder för sig själv.
tänker mer på formeln, att 10 står för höjden i cylindern? Om jag inte har fel
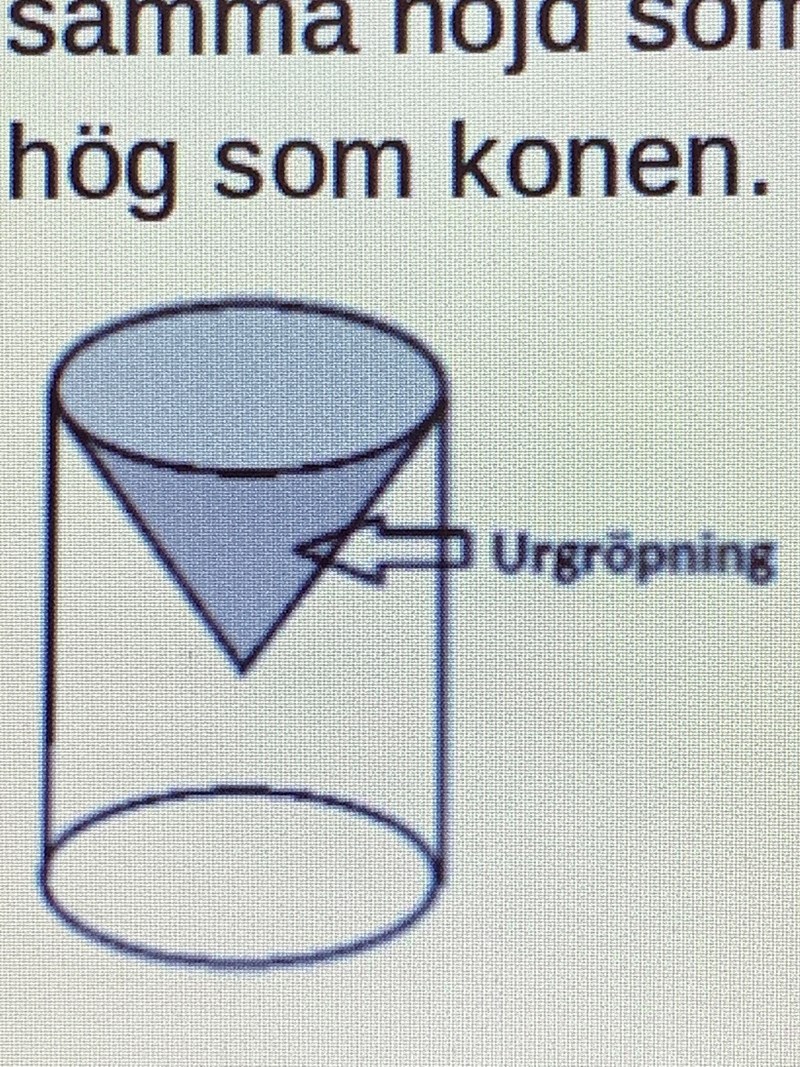
Rita en egen figur och för in beteckningarna. Den urgröpta cylinderns volym = cylinderns ursprungliga volym - konens volym
något såhär?
betyder det att man inte bör ha siffror med utan endast ”uttryck” ?
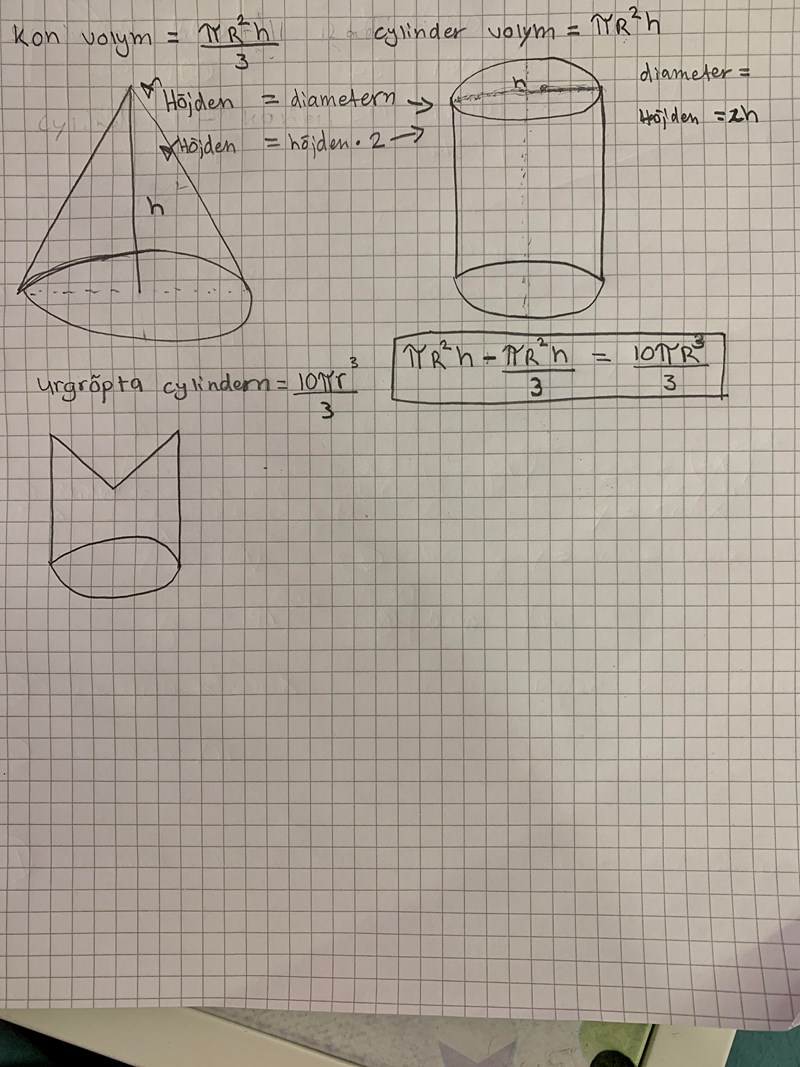
Nu har du använt bokstaven h både som cylinderns höjd och som konens höjd, men dessa höjder är inte lika. Både cylindern och konen har höjder som beror på radien. Kan du justera formlerna så att man kan se detta?
Jag skrev att konens höjd är H och cylinderns höjd är 2H asså dubbelt så hög som konen är.
Vilka andra sätt kan man beskriva det isåfall?
har suttit med denna uppgift i snart 1 och en halv timme, tror jag blir blind för svaret eller nåt.
Din lösning är svår att följa och den inramade ekvationen ekvationen stämmer inte - konen och cylindern har olika höjd.
Cylinderns volym:
Konens volym:
Jaha och om man subtraherar cylindern med konen så blir det svaret då?
Tack så jätte mycket, förstår det nu!!



