Sambandet mellan en lådas bottenarea, höjd och volym!
Vi började med detta i skolan igår och eftersom jag varit sjuk så behöver jag hjälp asap!
men jag tänker på 1a) 10 x 15 =150cm2 och 1b) ska jag bara dividera 1cm på vardera sida eller? Så alltså 13 x 8 = 104 cm2?
2. vill jag gärna få hjälp med hur man tänker!!

Vad blir lådans längd, bredd och höjd om den bortklippta kvadratens sida är x?
Vi började med detta igår och eftersom jag har varit sjuk behöver jag hjälp. Men 1a bör ju vara 10 x 15 = 150 cm2?
Ja det stämmer på 1 b) hur har du tänkt då? Kan du på liknande sätt resonera kring 2a) b) och c)?
Jag uppdaterade inlägget, kicka gärna upp där
På b) är det inte rätt eftersom du bara tar bort en del av lämgden och bredden. Du får istället räkna ut arean av de bortklippta kvadraterna och subtrahera detta från den totala arean(om hörnen varit kvar)
På 2a tänker jag samma att lådans längd är 15cm eftersom längden inte ändras?? Bredden bör ju även vara samma, men höjden har jag problem med...
Men arean på dem bortklippta delarna bör vara 1 x 1?
Höjden bildas av en del av längden och bredden, lådan bildas genom att vika upp kanterna. De bortklippta kvadraterna gör att lådans hörn inte överlappar varann. Så bredd, längd och höjd beror av de bortklippta kvadraternas storlek
Casper0505 skrev:Men arean på dem bortklippta delarna bör vara 1 x 1?
Ja precis och sen har du fyra stycken sådanna som ska subtraheras
Kan du göra en uträkning som jag sedan kan följa? På 2a
Bredden blir 10-1-1=8cm så kan du räkna längden.
Arean blir 15*10 - 4*1*1 = 150 - 4 = 146
Blir det minus 2 eftersom där är två kanter? Vilken var den andra uträkningen till?
Blir längden 13 eftersom det finns två kanter så? Eller blir sen 16 för den är dubbelt så lång som bredden?
Ja det blir minus två eftersom det är två kanter, längden blir 13 eftersom den också har två bortklippta kanter. Vore konstigt om det klipps bort hörn och viks upp och den blir längre.
Den andra uträkningen var för 1b
Hur räknar man ut höjden då? Vet att längden är 13 och bredden 8! Så 13 x 8 = 104 sen fastnar jag?
Höjden blir den del som man viker upp, alltså den bortklippta kvadratens sida. Kan du se framför dig hur lådan viks?
Det jag inte kan :( men när man vek lådan så försvann det 2 ifrån längden och 2 ifrån bredden? Menas det på att höjden blir det som är över? Alltså 2 x 2?
Höjden blir det som blev över ja, men eftersom det behövs fyra kanter till lådan så blir höjden 1cm brevid uppgift 2 i din bild så visas lådan när den är ihopvikt.
Okej, sen blir volymen 13 x 8 x 1 = 104 cm3?
Ja precis. Sen på 4) så gör du likadant men med olika storlekar på den bortklippta kvadraten (du får räkna ut nya bredd, längd och höjd)
Men eftersom volymen ska bli så stor som möjligt ska jag klippa bort en stor del på varje hörn eller så liten så möjligt? För jag tänker ju att det finns tusen olika saker man kan räkna ut 4an till...
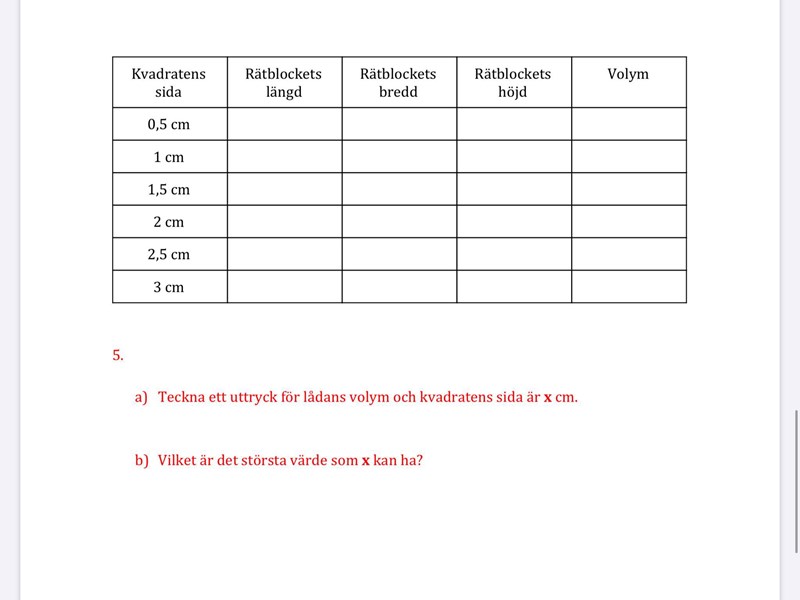
Har du räknat ut och fyllt i tabellen? Ja det finns oändligt många olika kombinationer man kan räkna ut. Men när du fyllt i tabellen så ser du kanske något samband för när det blir så stor volym som möjligt


