Sammansatt funktion + injektiv/surjektiv
Behöver lite vägledning för denna uppgift:
f:ℝ→[−4,∞[ (OBS !!! Vad betyder det att 2a haken är vänd åt samma håll som den 1a?)
f(x)=−3cos(πx)2−2
g:ℝ→ℝ
g(x)=5x4.
Den sammansatta funktionen h av f och g, uppfyller h(x)=f(g(x)) för alla x i deras definitionsmängd.
1) Vad är uttrycket för h(x)?
JAG får det till att h(x)=(((-3*cos(pi*5x)/4)/2) - 2 ---STÄMMER DETTA??? Ingen idé att gå vidare om det inte är korrekt.
2) Beräkna h(3), h(4) och h(5). Inga svar i sinus/cosinusfunktion eller decimalform.
Är det bara att sätta in värdena 3,4 & 5 istället för X i funktionen från a (om den stämmer?) och behövs ngn extra beräkningsmetodik för att få ut svaren i rätt form?
Din notation är oklar.
Skall det vara
?
Du måste skriva läsliga formler, det här går inte att tyda. Skall det vara eller eller någon annan variant? Skall det vara (=20 oberoende av x) eller eller någon annan variant?
Smaragdalena skrev:Du måste skriva läsliga formler, det här går inte att tyda. Skall det vara eller eller någon annan variant? Skall det vara (=20 oberoende av x) eller eller någon annan variant?
Divisionstecknen hade fallit bort.
f(x)=−3cos(πx)/2 −2, och g:ℝ→ℝ enligt g(x)=5x/4.
Hakparentes som pekar in mot siffran betyder att det värdet är med i mängden, och om den pekar ut från siffran är det inte med i mängden, alltså sträng olikhet. Eftersom oändligheten inte är ett tal, och alltså inte kan ingå i en definitionsmängd, så pekar den alltid utåt. Ex
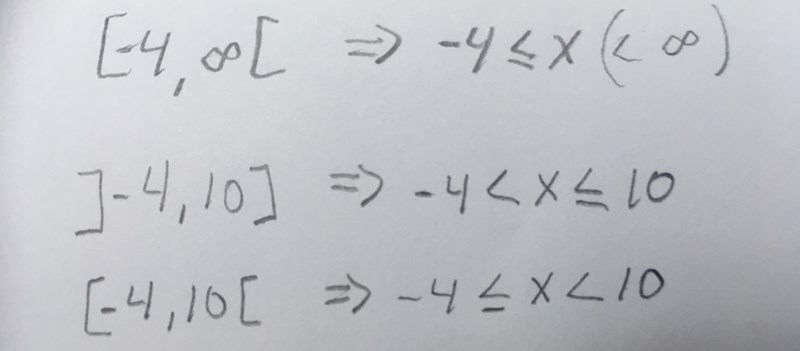
Din a-uppgift ser rätt ut, och det du måste tänka på i b för att få exakt form är att räkna ut vad cos v blir mha enhetscirkel/formelblad, och inte miniräknare.
Micimacko skrev:Hakparentes som pekar in mot siffran betyder att det värdet är med i mängden, och om den pekar ut från siffran är det inte med i mängden, alltså sträng olikhet. Eftersom oändligheten inte är ett tal, och alltså inte kan ingå i en definitionsmängd, så pekar den alltid utåt. Ex
Din a-uppgift ser rätt ut, och det du måste tänka på i b för att få exakt form är att räkna ut vad cos v blir mha enhetscirkel/formelblad, och inte miniräknare.
så h(x)=(((-3cos(pi*5x)/4)/2) - 2, när f(x)=(−3cos(πx)/2)−2, och g:ℝ→ℝ enligt g(x)=5x/4 ?
Micimacko skrev:Ja
Finns det ngt formelblad som är att föredra?
Jag tycker det är bättre att lära sig rita upp på enhetscirkeln.
Finns det ngt formelblad som är att föredra?
Självklart det som du får ta med dig när du skriver NPi Ma4. Det finns t ex på formelsamlingen.se
EDIT: och jag håller med om att man bör lära sig använda enhetscirkeln
Smaragdalena skrev:Finns det ngt formelblad som är att föredra?
Självklart det som du får ta med dig när du skriver NPi Ma4. Det finns t ex på formelsamlingen.se
EDIT: och jag håller med om att man bör lära sig använda enhetscirkeln
Ska beräkna värdet av h(3)=x nu.
Är det så enkelt att jag kan ersätta "cos pi" med (-1) eller ska jag räkna "cos 180 * x" ) och sedan få fram ett värde på cos?
EDIT: la till bortsprunget minustecken
Smaragdalena skrev:
Självklart - my bad :-)
Men det är alltså så pass "enkelt" att lösa uppgiften genom att bara ersätta "cos pi" med "1" och sedan fixa beräkningen?
Christian67 skrev:Smaragdalena skrev:Självklart - my bad :-)
Men det är alltså så pass "enkelt" att lösa uppgiften genom att bara ersätta "cos pi" med "1" och sedan fixa beräkningen?
Beräkning av h(3), h(4) & h(5) ger -61/8, -19/2 & -91/8
Tacksam om ngn kan bekräfta om det blev rätt eller om jag tänkt fel.
OBS jag hade tappat bort ett minustecken
Beräkning av h(3), h(4) & h(5) ger -61/8, -19/2 & -91/8
Tacksam om ngn kan bekräfta om det blev rätt eller om jag tänkt fel.
Alla ser ut att vara fel. Visa hur du har räknat, så kan vi hjälpa dig att hitta var det har blivit fel.
Smaragdalena skrev:OBS jag hade tappat bort ett minustecken
Beräkning av h(3), h(4) & h(5) ger -61/8, -19/2 & -91/8
Tacksam om ngn kan bekräfta om det blev rätt eller om jag tänkt fel.Alla ser ut att vara fel. Visa hur du har räknat, så kan vi hjälpa dig att hitta var det har blivit fel.
till att börja med ersatte jag (cos pi) med "1" ---- men det kanske blev fel? För h(3) skulle funktionen då bli ((-3*"1"*((5*3)/4))/2) -2 ==> -61/8
Om jag däremot använder en annan metod och räknar att (cos pi) = cos 180 för jag ut att h(3)=(-3/2*roten ur 2) - 2 (vilket sedan kanske kan förenklas)?
Du skall beräkna värdet av uttrycket för x=3. Börja med att beräkna värdet av för x=3.
Smaragdalena skrev:Du skall beräkna värdet av uttrycket för x=3. Börja med att beräkna värdet av för x=3.
blir det -1/4?
Menar du att vinkeln blir -(1/4)*pi? Isf ja.
Micimacko skrev:Menar du att vinkeln blir -(1/4)*pi? Isf ja.
kan det skrivas som -(1/roten ur 2)?
Christian67 skrev:Smaragdalena skrev:Du skall beräkna värdet av uttrycket för x=3. Börja med att beräkna värdet av för x=3.
blir det -1/4?
Nej, du verkar bara ha beräknat vinkeln men tappat bort . Vilket värde har ?
Smaragdalena skrev:Christian67 skrev:Smaragdalena skrev:Du skall beräkna värdet av uttrycket för x=3. Börja med att beräkna värdet av för x=3.
blir det -1/4?
Nej, du verkar bara ha beräknat vinkeln men tappat bort . Vilket värde har ?
-1/roten ur 2?
Rita en enhetscirkel.
Micimacko skrev:Rita en enhetscirkel.
Enligt enhetscirkeln är väl X-värdet för cos(pi/4) (roten ur 2/2)
innebär det att värdet för cos(−π/4) är (-roten ur 2/2)?
Smaragdalena skrev:Christian67 skrev:Smaragdalena skrev:Du skall beräkna värdet av uttrycket för x=3. Börja med att beräkna värdet av för x=3.
blir det -1/4?
Nej, du verkar bara ha beräknat vinkeln men tappat bort . Vilket värde har ?
Nu snurrar det rejält -dags att sova tror jag :-)
Men visst blir väl cos(-π/4)=1?
Christian67 skrev:Smaragdalena skrev:Christian67 skrev:Smaragdalena skrev:Du skall beräkna värdet av uttrycket för x=3. Börja med att beräkna värdet av för x=3.
blir det -1/4?
Nej, du verkar bara ha beräknat vinkeln men tappat bort . Vilket värde har ?
-1/roten ur 2?
OK - nya tag
värdet för cos(5*pi*3)/4 blir Roten ur 2/2 ? Rätt/Fel?
värdet för hela uttrycket borde då bli ((-3*roten ur 2)/4) -2 ? Rätt/Fel
Det ser ut att vara rätt värde på h(3). Vilket värde har h(4) och h(5)?
Du har rätt i att men det är vanligare att man skriver det som där man har förkortat med (och som är det värde man får när man använder sig av "en halv kvadrat").
Smaragdalena skrev:Det ser ut att vara rätt värde på h(3). Vilket värde har h(4) och h(5)?
Du har rätt i att men det är vanligare att man skriver det som där man har förkortat med (och som är det värde man får när man använder sig av "en halv kvadrat").
Jag får det till att h(3) och h(5) får samma värde - stämmer det?
för h(4) blir värdet -7/2 - stämmer det?
Jag får det till att h(3) och h(5) får samma värde - stämmer det?
för h(4) blir värdet -7/2 - stämmer det?
Snälla låt oss slippa gissa - visa steg för steg hur du har räknat, i stället för att bara slänga fram svaret utan motivering. Vilket värde har cosinus-termen i de båda fallen?
Smaragdalena skrev:Jag får det till att h(3) och h(5) får samma värde - stämmer det?
för h(4) blir värdet -7/2 - stämmer det?Snälla låt oss slippa gissa - visa steg för steg hur du har räknat, i stället för att bara slänga fram svaret utan motivering. Vilket värde har cosinus-termen i de båda fallen?
för h(4 ) får jag "cosinusvärdet" till (cos 5*pi) =-1
för h(5) blir cosinusvärdet (cos(25*pi)/4)=1/roten ur 2
För h(4) blir cosinusvärdet -1 eftersom 4 i täljaren och 4 i nämnaren tar ut varandra. För h(5) gäller det att , d v s samma som för f(3), så h(5)=h(3), det stämmer.
Smaragdalena skrev:För h(4) blir cosinusvärdet -1 eftersom 4 i täljaren och 4 i nämnaren tar ut varandra. För h(5) gäller det att , d v s samma som för f(3), så h(5)=h(3), det stämmer.
OK - se mina beräkningar (bild)
Vv bekräfta om det blev rätt så att jag kan fortsätta till uppgiften att bestämma definitions- & målmängden för h :-)
Du borde förenkla uttrycken för h(3) och h(5).
Smaragdalena skrev:Du borde förenkla uttrycken för h(3) och h(5).
Så här då - eller kan det förenklas ytterligare?
Jag skulle föredra att ha det som ett bråk med allting så faktoriserat som möjligt, är alltså bättre än . Men det är inte säkert att ditt facit tänker som jag.
Smaragdalena skrev:Jag skulle föredra att ha det som ett bråk med allting så faktoriserat som möjligt, är alltså bättre än . Men det är inte säkert att ditt facit tänker som jag.
Jag får nog fråga helt enkelt - onödigt att jobba vidare om det man gjort fram till nu inte är 100% korrekt.
Jag tror att det du gjort hittills är korrekt, så du kan fortsätta med nästa fråga. Gör en ny tråd om den så man slipper scrolla så mycket, och länka till den här tråden. Skriv värdena du har kommmit fram till i förstainlägget, så att man inte behöver leta efter dem. /moderator



