Sannolikhet med träddiagram
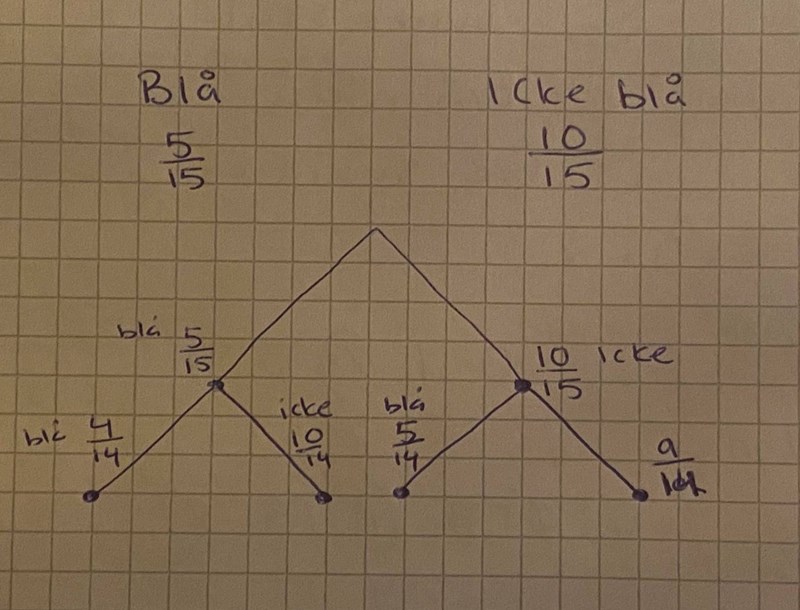
I en påse finns 4 röda, 5 blå och 6 gröna kulor. Plocka utan att titta, upp två kulor. Hur stor är sannolikheten att minst en kula är blå? 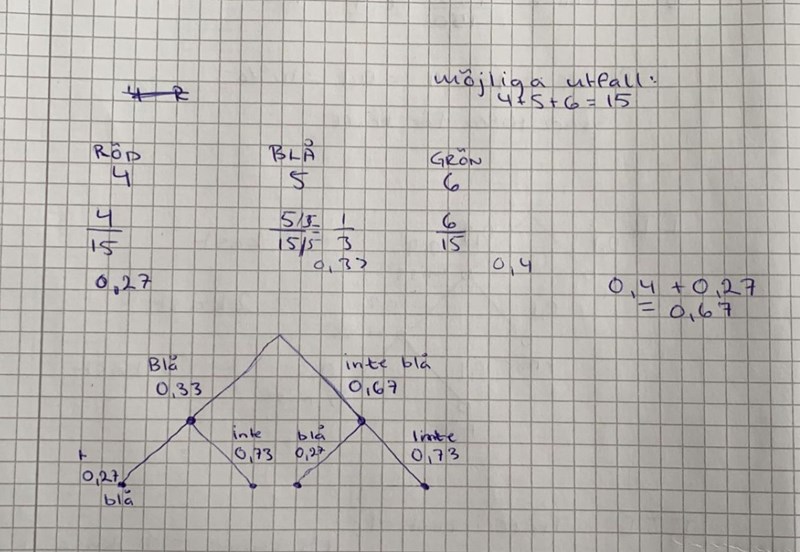
Om jag tolkat ditt träd rätt är sannolikheten att kula nummer 2 är blå opåverkad av om man drog en blå kula först eller inte, eftersom sannolikheten för blå kula nummer 2 tycks vara 0,73 oavsett. Känns det rimligt?
I varje fall: om du tar sannolikheten för icke-blå kula nummer 1 gånger sannolikheten för icke-blå kula nummer 2 har du fått fram sannolikheten att ingen tagen kula är blå. Sannolikheten att minst en tagen kula är blå är dess komplementhändelse.
Hej.
Dina sannolikheter stämmer inte, på flera olika sätt.
- Du bör räkna med bråktal istället för med avrundade närmevärden, annars kommer du inte att kunna ge ett exakt svar Till exempel är sannolikheten att första dragningen ger en blå kula lika med 5/15 = 1/3, vilket inte är lika med 0,33.
- Sedan räknar du fel på sannolikheterna för dragning 2, du måste då ta hänsyn till att det bara är 14 kulor kvar i påsen.
Jag får inte till det..
Innan första dragningen finns det 15 kulor i påsen: 5 blåa och 10 andra.
Sannolikheten att dra en blå kula är då 5/15 och sannolikheten att dra en annan färg är 10/15.
Efter första dragningen så kommer det att finnas två olika situationer, beroende på vad som hände i första dragningen:
- Första dragnigen gav en blå kula. Då ligger det 14 kulor i påsen: 4 blåa och 10 andra. Sannolikheten att dra en blå kula är då [du fyller i] och sannolikheten att dra en annan färg är [du fyller i].
- Första dragnigen gav en annan färg. Då ligger det 14 kulor i påsen: 5 blåa och 9 andra. Sannolikheten att då dra en blå kula är [du fyller i] och sannolikheten att dra en annan färg är [du fyller i].
Kan du nu fylla i de sannolikheter som saknas?
Sedan finns det ett enklare sätt att lösa uppgiften som baserar sig på komplementhändelse, men det kan vi ta senare.
Det är viktigt att du får kläm på det här med träddiagram.
1. Sannolikheten för att dra en blå kula 4/14 och icke blå 10/14
2. Sannolikheten för att dra en blå kula 5/14 och icke blå 9/14.
Bra, det stämmer.
Då kan du skriva in dessa bråkymtal på rätt ställen i träddiagrammet.
Visa ditt uppdaterade träddiagram.
Bra, nu ser det rätt ut.
- Vet du vad de fyra nedetsta punkterna i träddiagrammet betyder, dvs vilka utfall de motsvarar?
- Vet du vad sannolikheterna för utfallen som motsvarar de fyra nedersta punkterna är?
- Vet du hur du ska fortsätta härifrån?
1.De nedersta punkterna är utfall 2
2. Menar du i decimal och procentform?
3. nej det vet jag inte
- Tillstånd A motsvarar att första kulan är blå. Sannolikheten för detta är 5/15 = 1/3.
- Tillstånd B motsvarar att första kulan är av en annan färg. Sannolikheten för detta är 10/15 = 2/3.
- Tillstånd C motsvarar att första kulan var blå och att andra kulan var blå. Sannolikheten för detta är (1/3)*(4/14).
- Tillstånd D motsvarar att första kulan var blå och att andra kulan var av en annan färg. Sannolikheten för detta är (1/3)*(10/14).
- Tillstånd E motsvarar att första kulan var av en annan färg och att andra kulan var blå. Sannolikheten för detta är (2/3)*(5/14).
- Tillstånd F motsvarar att första kulan var av en annan färg och att andra kulan var av en annan färg. Sannolikheten för detta är (2/3)*(9/14).
Av dessa 4 sluttillstånd C, D, E och F är det 3 som uppfyller villkoret att minst en kula är blå.
Kan du säga vilka?
Kan du även säga hur stor sannolikheten är att något av dessa tre tillstånd inträffar?
I så fall har du klarat uppgiften.