Sannolikhet summa av valörer

Eftersom hon blandar kortleken i början, så kan jag väl strunta i att hon lägger åt sidan 13 av korten, eller måste jag räkna på att 13 kort försvinner, dvs att det är 39 kort kvar. Och efter detta beräkna P(summa 4)?
Jämför de två fallen:
a) Hon råkar lägga bort 4 kungar, 4 damer, 4 knektar + en tia.
b) Hon råkar lägga bort 4 ess, 4 tvåor, 4 treor + 3n fyra.
Blir P(summa 4) samma i både fallen?
Guuuben skrev:Jämför de två fallen:
a) Hon råkar lägga bort 4 kungar, 4 damer, 4 knektar + en tia.
b) Hon råkar lägga bort 4 ess, 4 tvåor, 4 treor + 3n fyra.
Blir P(summa 4) samma i både fallen?
Om hon råkar lägga bort 4 kungar, 4 damer, 4 knektar och en tia, hur ska jag beräkna summorna? Det blir ju jättemånga kombinationer
Ja, du kan strunta i att några är lagda åt sidan. Visst, korten man drar kommer bero på vilka som lagts undan, men vi vet ju inte vilka kort som är borta. Därför är situationen rent sannolikhetsmässigt samma som om alla kort är tillgängliga, att vi helt enkelt drar 2 kort av 52. Om det däremot stått "bland de slängda finns två kungar" t.ex, då hade det skruvat på sannolikheten, eftersom vi får veta att dessa kort inte kan dras.
Men hur blir uträkningen för detta problem, jag har fastnat och kommer inte vidare...
Hur kan jag beräkna att summan blir 4
Vilka kombinationer av kort ger summa 4?
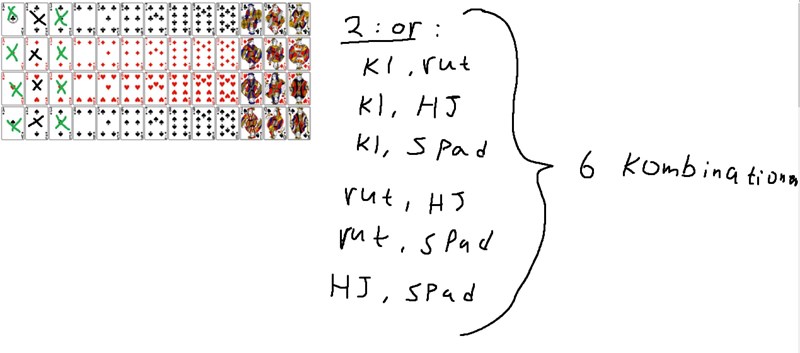
Vet dock inte hur jag beräknar antalet kombinationer för (Ess + 3:a)
Först väljer du ett ess, på hur många sätt kan du göra det? Sen väljer du en trea.
Ettan kan vara vilken som helst av 4 färger. Trean kan vara vilken som helst av 4 färger. Hur många kombinationer finns det?
Är lite ringrostig på kombinatorik men antalet kombinationer för essen och treorna borde väl bli
4*4 = 16 st
theg0d321 skrev:Är lite ringrostig på kombinatorik men antalet kombinationer för essen och treorna borde väl bli
4*4 = 16 st
Stämmer. Hur många gynnsamma utfall finns det totalt?
Om jag tänker rätt så borde det så ut på följande vis:
Antalet gynsamma utfall = (Antalet kombinationer för 2:or + Antalet kombinationer för Ess och treor)
Antalet gynsamma utfall = 6 + 16 = 22
Hur tänker jag kring antalet möjliga utfall?





