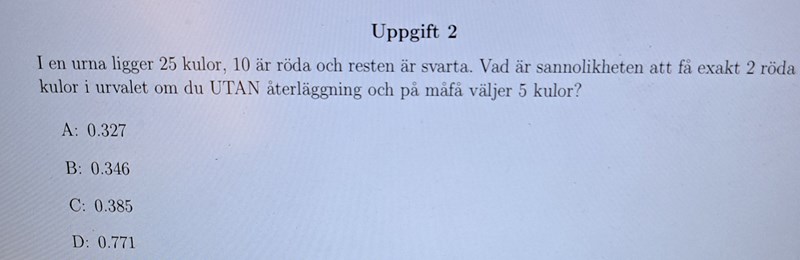
Sannolikheten att få exakt 2 röda kulor i urvalet om du utan återläggning på måfå väljer 5 kulor

Hypergeometrisk fördelning $X\in Hyp(N,n,m)$ är din kompis, om du inte vill rita ett träddiagram som man gjorde i högstadiet. 

sictransit skrev:

Hypergeometrisk fördelning $X\in Hyp(N,n,m)$ är din kompis, om du inte vill rita ett träddiagram som man gjorde i högstadiet. 

Jag förstår! Ja det verkar rimligt. N är alltså antalet kulor dvs 25 st , sen vet jag inte n och m står för?

destiny99 skrev:

sictransit skrev:

Hypergeometrisk fördelning $X\in Hyp(N,n,m)$ är din kompis, om du inte vill rita ett träddiagram som man gjorde i högstadiet. 

Jag förstår! Ja det verkar rimligt. N är alltså antalet kulor dvs 25 st , sen vet jag inte n och m står för?

Kika i den länkade artikeln. Onödigt att jag kopierar in texten här. I den står också hur du rent praktiskt räknar ut det.

Om man håller sig på en lägre nivå kan man väl tänka så här:

1. Hur många olika sätt kan man få exakt två röda på?
2. Vad är sannolikheten för ett av dessa sätt (till exempel att kula 1-2 är röda och kula 3-5 är svarta)?

Sedan multiplicerar man dessa tal. Det ger mig alternativ C.

SvanteR skrev:

Om man håller sig på en lägre nivå kan man väl tänka så här:

1. Hur många olika sätt kan man få exakt två röda på?
2. Vad är sannolikheten för ett av dessa sätt (till exempel att kula 1-2 är röda och kula 3-5 är svarta)?

Sedan multiplicerar man dessa tal. Det ger mig alternativ C.

1. Är n över k dvs 25 över 5? Men 2. Vet jag inte riktigt hur man ställer upp. Jag förstår dock med hypergeometriska fördelningen som länkades ovan.

Jag kände att jag behövde förstå det här själv, särskilt efter SvanteR:s svar som fick mig att inse att jag nog inte hade koll.

Sannolikhet är svårt, men jag är van att tänka binärt, så jag tog den omvägen.

Hur många 25-bitars binära tal kan man konstruera med 10 ettor (röda kulor) och 15 nollor (svarta kulor)?

Jo, vi skall helt enkelt peta in ettor i någon av de 25 positionerna, så blir resten nollor med automatik: $\left(\begin{array}{c}25\\ 10\end{array}\right)=3268760$

De gynnsamma utfallen är de som innehåller exakt 2 ettor i de första fem positionerna: $\left(\begin{array}{c}5\\ 2\end{array}\right)=10$

11000
10100
10010
10001
01100
01010
01001
00110
00101
00011

De får alltså motsvara de fall där vi drar precis två röda bland de fem vi väljer. 

Sedan har vi 8 ettor kvar att stoppa in i resterande 20 positioner: $\left(\begin{array}{c}20\\ 8\end{array}\right)=125970$

Vi har alltså $10\times 125970=1259700$ gynnsamma utfall.

P(2 röda) torde alltså bli: $\frac{1259700}{3268760}\approx \boxed{0,385}$

destiny99 skrev:

SvanteR skrev:

Om man håller sig på en lägre nivå kan man väl tänka så här:

1. Hur många olika sätt kan man få exakt två röda på?
2. Vad är sannolikheten för ett av dessa sätt (till exempel att kula 1-2 är röda och kula 3-5 är svarta)?

Sedan multiplicerar man dessa tal. Det ger mig alternativ C.

1. Är n över k dvs 25 över 5? Men 2. Vet jag inte riktigt hur man ställer upp. Jag förstår dock med hypergeometriska fördelningen som länkades ovan.

Jag tänkte så här:

1. är 5 över 2, dvs (5*4)/(2*1) = 10 (se förklaringen från sictransit ovan).

2. Sedan kan man till exempel beräkna sannolikheten för att den första och den andra kulan är röd medan kula 3-5 är svarta. Den ges av $\frac{10}{25}*\frac{9}{24}*\frac{15}{23}*\frac{14}{22}*\frac{13}{21}\approx 0,0385$

Sannolikheten för exakt två röda ges sedan av 10*0,0385 =0,385 

Bra tänkt. Tack. Har inte kontrollerat, men gissar du får ett ungefärligt värde vilket är gott nog för att besvara frågan. 

SvanteR skrev:

destiny99 skrev:

Visa föregående citat

SvanteR skrev:

Om man håller sig på en lägre nivå kan man väl tänka så här:

1. Hur många olika sätt kan man få exakt två röda på?
2. Vad är sannolikheten för ett av dessa sätt (till exempel att kula 1-2 är röda och kula 3-5 är svarta)?

Sedan multiplicerar man dessa tal. Det ger mig alternativ C.

1. Är n över k dvs 25 över 5? Men 2. Vet jag inte riktigt hur man ställer upp. Jag förstår dock med hypergeometriska fördelningen som länkades ovan.

Jag tänkte så här:

1. är 5 över 2, dvs (5*4)/(2*1) = 10 (se förklaringen från sictransit ovan).

2. Sedan kan man till exempel beräkna sannolikheten för att den första och den andra kulan är röd medan kula 3-5 är svarta. Den ges av $\frac{10}{25}*\frac{9}{24}*\frac{15}{23}*\frac{14}{22}*\frac{13}{21}\approx 0,0385$

Sannolikheten för exakt två röda ges sedan av 10*0,0385 =0,385 

Hm ok jag förstår inte det här sättet helt hundraprocent. Men jag läste på wikipedia om hypergeometrisk fördelning och lyckades förstå hur den används tillsammans med denna uppgift.  Tackar ändå för hjälpen!