Sannolikheten att få två ettor med två tärningar
Det är möjligt att en liknande kluring varit med tidigare, men kanske inte med tärningar (den brukar presenteras med två möjliga utfall, som "son eller dotter" eller "krona eller klave").
1. Om du kastar två sexsidiga tärningar, en röd och en blå, vilken är sannolikheten att båda visar ettor?
2. Om du kastar två sexsidiga tärningar, en röd och en blå, och den röda blir en etta, vilken är sannolikheten att båda visar ettor?
3. Om du kastar två sexsidiga tärningar och minst en av dem visar en etta, vilken är sannolikheten att den andra också visar en etta?
Om jag minns detta rätt så fungerar det såhär:
Sannolikheten att en sexsidig tärning visar ett specifikt nummer, t.ex. 1, är 1/6. Sannolikheten att två sexsidiga tärningar visar samma värde är 1/6 * 1/6 eller 1/36.
Om en av tärningarna med 100% säkerhet visar värdet 1 så är sannolikheten att båda visar nr.1 lika med 1 * 1/6 eller 1/6
1. 1/36
2. 1/6
3. 1/11
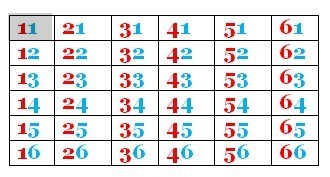
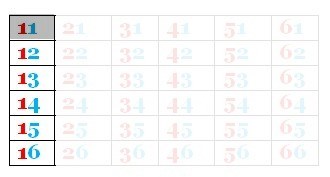
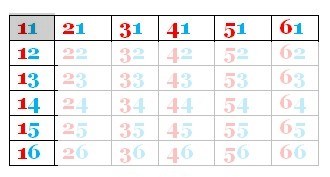
Alla 36 möjligheter är lika sannolika. I uppgift 2) och 3) har du på förhand uteslutit en del av de 36 möjligheterna.
En liknande, om vi har tre slantar där varje sida har samma sannolikhet att hamna upp när man singlar dom. Givet att vi vet att åtminstone 2 av dom hamnade på samma sida, hur stor är sannolikheten att alla tre visar samma sida?
Yngve skrev :1. 1/36
2. 1/6
3. 1/11
Hur kommer du fram till svaret på 3:an? Borde inte det vara samma som 2?
Angående 3:an, se Bubos bild.
Slantarna kan ju vara AAB, ABA, BAA eller AAA så svaret blir 1/4.
Här är en intressant variant på samma tema:
Ett par föräldrar har två barn. Minst ett är en son. Hur stor är sannolikheten att andra barnet är en son? (Jag lämnar den här som lätt övning...)
Nästa fråga: Ett par föräldrar har två barn. Minst ett är en son som är född en onsdag. Hur stor är sannolikheten att andra barnet är en son?
Minounderstand skrev :Yngve skrev :1. 1/36
2. 1/6
3. 1/11
Hur kommer du fram till svaret på 3:an? Borde inte det vara samma som 2?
Nej det är inte samma.
Det finns 11 möjliga utfall där minst en av tärningarna visar en etta (11, 12, 13, 14, 15, 16, 21, 31, 41 51, 61). Endast ett av dessa möjliga utfall är gynnsamt (11).
Se Bubos utmärkta illustration.
Bubo skrev :Slantarna kan ju vara AAB, ABA, BAA eller AAA så svaret blir 1/4.
Här är en intressant variant på samma tema:
Ett par föräldrar har två barn. Minst ett är en son. Hur stor är sannolikheten att andra barnet är en son? (Jag lämnar den här som lätt övning...)
Nästa fråga: Ett par föräldrar har två barn. Minst ett är en son som är född en onsdag. Hur stor är sannolikheten att andra barnet är en son?
Jag säger 13/27.
Japp.
Jag tycker att det här är ett praktexempel på hur "sunt förnuft" kan leda fel. Mitt "sunda förnuft" säger att veckodagen är oväsentlig, så svaret "borde" vara detsamma på mina två frågor.
Bubo skrev :Japp.
Jag tycker att det här är ett praktexempel på hur "sunt förnuft" kan leda fel. Mitt "sunda förnuft" säger att veckodagen är oväsentlig, så svaret "borde" vara detsamma på mina två frågor.
Förklaring önskas! Varför blir det inte 1/11 igen?
Första frågan: Sannolikheten att även andra barnet är en son är 1/3.
(En av tre lika stora möjligheter, se figur)
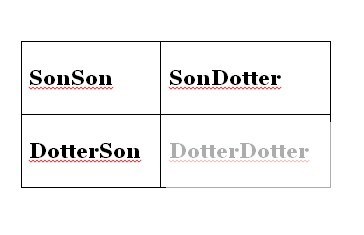
Andra frågan: Vi vet redan att minst en son är född en onsdag. Kön och veckodagar kan kombineras på 2^2 * 7^2 sätt = 4*49 sätt, men hur många av dessa innehåller en son som är född en onsdag?
a) SonDotter - 7 möjligheter
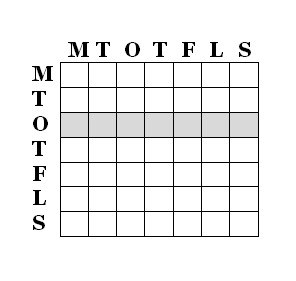b) DotterSon - 7 möjligheter
c) DotterDotter - 0 möjligheter
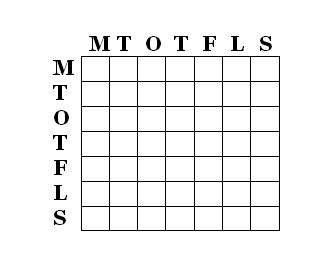
d) SonSon - 13 möjligheter
Alltså 13 av 27.
Oj, jag var tydligen kvar i tärningarnas värld - vilket jättefel! Ändringen från 3/4 1/3 till 13/27 är åtminstone något mindre absurd än den förändring jag (felaktigt) hade fått i huvudet.
EDIT: Rättade till ett nästan lika stort tankefel. Heter det headdesk eller facepalm?
smaragdalena skrev :Oj, jag var tydligen kvar i tärningarnas värld - vilket jättefel! Ändringen från 3/4 till 13/27 är åtminstone något mindre absurd än den förändring jag (felaktigt) hade fått i huvudet.
*från 1/3 till 13/27.
Jag gjorde en simulering på 999 tärningskast (första fliken) och 999 myntsinglingar (andra fliken): https://docs.google.com/spreadsheets/d/1eWpYcu2wxfcPfUngxX0QD-UQ82sZeiM6n5Dx3lnVcyA/edit?usp=sharing
"Född på en onsdag" och liknande varianter reduceras enligt wikipedia till
P(båda har samma kön om minst en med det könet har egenskap q) = (2-q)/(4-q)
där q är sannolikheten för att vara till exempel född på en onsdag (q = 1/7), född 1 januari (q = 1/365) eller född i en udda månad (q = 1/2 om vi antar att alla månader har lika många dagar). Eller för den delen "född med en hög hatt sjungandes en show-tune" (q är så gott som noll).
Jag såg just en intressant variant som jag inte tänkt på förut:
Jag drar ett kort ur en kortlek, och ytterligare ett kort ur en likadan kortlek.
Till Alice säger jag "minst ett av korten är rött. Vilken är sannolikheten att båda korten är röda?"
Till Bob säger jag "minst ett av korten är en hjärter. Vilken är sannolikheten att båda korten är hjärter?"
Till Carl säger jag "minst ett av korten är en dam. Vilken är sannolikheten att båda korten är en dam?"
Till David säger jag "minst ett av korten är hjärter dam. Vilken är sannolikheten att båda korten är hjärter dam?"
David ska göra både facepalm och headdesk om han missar.
Bubo skrev :David ska göra både facepalm och headdesk om han missar.
Ja, särskilt om han läst den här tråden.
Om sannolikheten att få ett visst utfall är 1/n, så är svaret på frågan "hur stor sannolikhet är det att båda dragningarna ger det utfallet, om du vet att minst en gör det" lika med 1/(2n-1).
Så David borde säga 1/(2*52-1) = 1/103.
Jag läser dåligt - jag trodde det gällde EN kortlek... :-)
Bubo skrev :Jag läser dåligt - jag trodde det gällde EN kortlek... :-)
Aha. Ja, då ska David både slå sig själv i ansiktet och få några extra örfilar av Alice, Bob och Carl.
Yngve skrev :Minounderstand skrev :Yngve skrev :1. 1/36
2. 1/6
3. 1/11
Hur kommer du fram till svaret på 3:an? Borde inte det vara samma som 2?
Nej det är inte samma.
Det finns 11 möjliga utfall där minst en av tärningarna visar en etta (11, 12, 13, 14, 15, 16, 21, 31, 41 51, 61). Endast ett av dessa möjliga utfall är gynnsamt (11).
Se Bubos utmärkta illustration.
Ah, nu föll det på plats. Tolkade den tredje frågan som en omformulering av den andra, varför kan man ju fråga sig. :(
Bubo skrev:Slantarna kan ju vara AAB, ABA, BAA eller AAA så svaret blir 1/4.
Här är en intressant variant på samma tema:
Ett par föräldrar har två barn. Minst ett är en son. Hur stor är sannolikheten att andra barnet är en son? (Jag lämnar den här som lätt övning...)
Nästa fråga: Ett par föräldrar har två barn. Minst ett är en son som är född en onsdag. Hur stor är sannolikheten att andra barnet är en son?
Föräldrar och barn... Tolkningsfråga kanske men mina svar är 2/3 resp. 20/27. Någon som är med på hur jag tänkte?
