Sannolikhets/ kombinatorik(🤢 🤮)problem
Hej!
Jag undrade om följande problem kunde lösas med sannolikhet:
https://open.kattis.com/problems/dicecup
Just nu har jag löst det klassisk, men jag undrar om det är en formel för att lösa det snabbare än med en HashMap?
Jag tänkte att först måste man nog bestämma på hur många sätt får vi varje tal -tärningar lär väl olika (hatade kombinatorik 😭!), och då dela det med alla möjliga utfall. Men även då, skulle vi inte behöva en HashMap eller en frequency array för att besvara frågan?
Vad tycker ni?
Hur menar du "med sannolikhet"? Genom att slå tärningarna en miljard gånger och kolla vad som blir vanligast?
Det låter som en bra idé, om inte för långt!
Som sagt jag gjorde en samling av värdarna, och valde ut den vanligaste
med 6 och 6 blir det
{2=1, 3=2, 4=3, 5=4, 6=5, 7=6, 8=5, 9=4, 10=3, 11=2, 12=1}
6 och 4 sidor blir det
{2=1, 3=2, 4=3, 5=4, 6=4, 7=4, 8=3, 9=2, 10=1}
Annars om det finns en formeln?
dajamanté skrev:Det låter som en bra idé, om inte för långt!
Som sagt jag gjorde en samling av värdarna, och valde ut den vanligaste
med 6 och 6 blir det
{2=1, 3=2, 4=3, 5=4, 6=5, 7=6, 8=5, 9=4, 10=3, 11=2, 12=1}
6 och 4 sidor blir det
{2=1, 3=2, 4=3, 5=4, 6=4, 7=4, 8=3, 9=2, 10=1}
Annars om det finns en formeln?
Nja, min idé är bara bra om man inte kan räkna ut det på något annat sätt. Din metod är bra, men ännu bättre är att arbeta fram en formel matematiskt. Man ser redan ett mönster i dina två exempel. Om du skriver talen i en tabell (ena tärningen lodrätt och andra tärningen vågrätt) och ser vilken summa som är vanligast så ser du det kanske tydligare.
Med min ökända teknik av den blöta öga, tomma hjärna kan jag gissa att det kommer att likna en normalfördelning?
dajamanté skrev:Med min ökända teknik av den blöta öga, tomma hjärna kan jag gissa att det kommer att likna en normalfördelning?
Den gissningen är inte helt fel: om man har riktigt många tärningar så närmar sig den resulterande binomialfördelningen en normalfördelning. Men här är det bara två tärningar, så normalfördelning är fel.
Men hur skulle du lösa, matematisk?
Om tärningarna har 8 respektive 15 sidor, så blir tabellen så här:
Har du en hypotes om hur man tänker sen?
Det verkar som... alla tal efter 8:an upprepas 8 gånger (?)
dajamanté skrev:Det verkar som... alla tal efter 8:an upprepas 8 gånger (?)
Inte alla, men vi ser att det största antalet sätt att få en viss summa är 8, och att det är några som uppnår det antalet.
Laguna skrev:dajamanté skrev:Det verkar som... alla tal efter 8:an upprepas 8 gånger (?)
Inte alla, men vi ser att det största antalet sätt att få en viss summa är 8, och att det är några som uppnår det antalet.
Jag men precis. Jag menade så.
Jag har sovit (mycket dåligt) på det. Varför är det så?
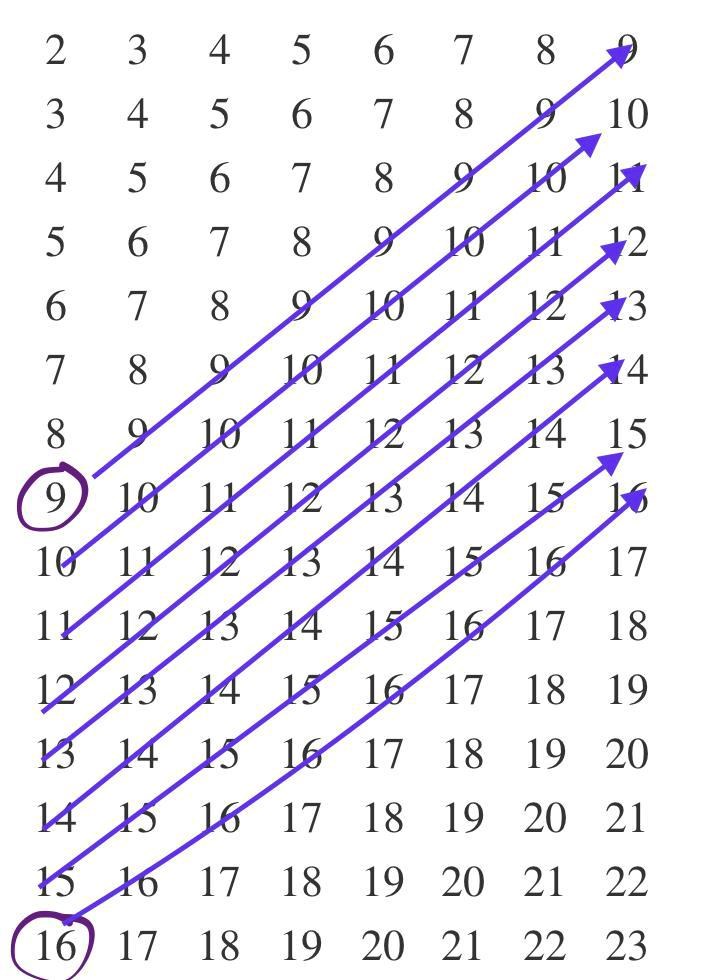
Om vi säger att antalet sidor är m och n, och m <= n, vilket är det största antalet sätt som någon summa kan bildas på?
Låt oss säga m-n då?
Men hur kan jag isolera vilka tal repeteras 8 gånger (i den här exempel)?
dajamanté skrev:Låt oss säga m-n då?
Men hur kan jag isolera vilka tal repeteras 8 gånger (i den här exempel)?
m-n kan inte vara rätt. Då skulle det bli noll för två likadana tärningar. Dessutom är det negativt i alla andra fall.
n-m + 1?... Jag verkligen ser inte.
m, helt enkelt.
Okej, tack för talamådet!
Så nu som vi du har listat ut att det var m, hur tar vi fram vilka tal återkommer m gånger?
Alla tal från och med m+1 till och med n+1
Nu som du säger det... det verkar rimligt.
Jag ska testa uppdaterade koden.
EDIT: vad om m = n?
dajamanté skrev:Nu som du säger det... det verkar rimligt.
Jag ska testa uppdaterade koden.
EDIT: vad om m = n?
Ja?
Låt oss titta på m=n=3
Då kommer alla tal från och med m+1=4 till och med n+1=4 vara de tal som förekommer flest gånger.
Det vill säga 4
Ja, det stämmer ju. Talet 4 är det tal som förekommer flest gånger. Antal gånger är som talet förekommer är 3 och det stämmer ju med att Laguna skrev att det skulle vara m.
Allt under förutsättning att m<=n som Laguna skrev.
Nu måste jag faktiskt tacka er mycket varmt!
Koden innan PA intervention:

koden efter PA intervention:






