Satslogik

Låt K vara "Jag kör till arbetet" och T vara "Jag blir trött".

Om vi inte bryr oss om skillnaderna i tempus så kan vi skriva

1. "Om jag kör till arbetet så kommer jag att bli trött" som $K\Rightarrow T$.
2. "Jag kör inte till arbetet" som $\lnot K$.
3. "Jag är inte trött" som $\lnot T$.

Problemet här är att tredje satsen inte följer av första och andra satsen.

Detta går att visa t.ex. med hjälp av en sanningstabell:

$\begin{array}{ccc}K&T&K\Rightarrow T\\S&S&S\\S&F&F\\F&S&S\\F&F&S\end{array}$

De två premisserna psssar in på både näst sista och sista raden i tabellen.

Det går alltså inte att säga huruvida $T$ är sann eller inte.

-------

Tillbakaöversatt till talspråk så kan jag mycket väl vara trött trots att jag inte kör till arbetet.

Enligt facit ska svaret bli att det ej är sant dock. Tack för förklaringen, jag jobbar vidare.

Precis som Yngve skrev, så kan man inte dra slutsatsen att jag inte är trött. Alltså är slutledningen inte giltig, precis som ditt facit säger.

Men som Yngve skriver så löser hon för $K\Rightarrow T$. Är det inte $(K\to T)\wedge \neg K\Rightarrow \neg T$ man ska räkna ut?

Plugghingsten, nu har du två olika trådar med identiska rubriker. Det är mycket förevirrande för oss som vill svara. Du kan själv rätta till dina rubriker genom att redigera dina förstainlägg. Gör det! /moderator

Typiskt, jag ber om ursäkt för detta! Tack för notisen. Dock hittar jag inte hur jag kan redigera  rubriken.

Var finner jag var jag kan redigera om inte där jag har markerat ovan?

UPDATE:

Jag vet inte hur men jag kan ändra det första inlägget och har gjort det nu. Kanske för att den är markerad som avklarad.

Oj, jag hade inte sett att det ena inlägget var så gammalt - det är bara inom 2 timmar man kan redigera själv, därefter kan en moderatorr hjälpa till. /moderator

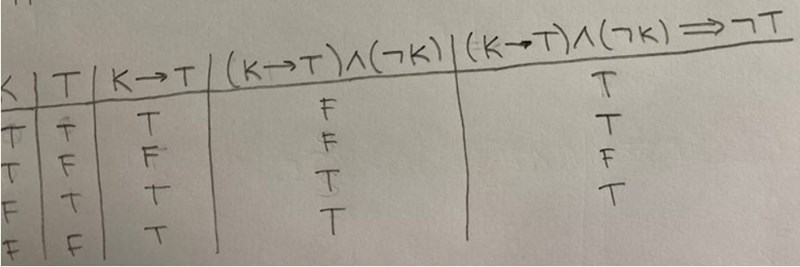
Det du har visat med din uppställning är just det att härledningen $(K\rightarrow T)\wedge \neg K\Rightarrow\neg T$ inte alltid har sanningsvärde SANT, vilket innebär att härledningen inte är giltig. Det fall för vilket härledningen har sanningsvärdet FALSKT är just det jag nämnde, nämligen $T\wedge\neg K$, dvs "Jag är trött (trots att) jag inte kör till arbetet".

Men gör gärna samma uppställning för följande härledning. Vad ser du då?

"Om jag kör till arbetet så kommer jag att bli trött"

"Jag är inte trött"

-----------------------------------------

$\therefore$ "Jag kör inte till arbetet"

Uppgiften du skrev ovan blir en tautologi. Det betyder att sanningsvärdet alltid är sann och därmed  är härledningen giltig.