Sätt y = x3 + 2. Beräkna dx/dy med implicit derivering och använd det för att hitta (f^-1)'(x)
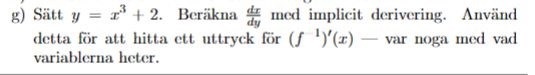
När jag försöker beräkna dx/dy med implicit derivering får jag vilket är fel, det ska bli . Så min första fråga är hur man ska göra för att få rätt dx/dy mha implicit derivering - Det löste sig, (men inte andra frågan)
Sen undrar jag också hur och varför man kan använda det för att få fram inversens derivata, som enligt facit bara är att sätta in inversa funktionen som x i .
f-1(f(x)) = x
y = f(x) => f-1(y) = x.
df-1(y)/dy = dx/dy = 1/(3x2). y = x3 + 2 => x = (y-2)1/3.
Kommer du vidare?
Jag fattar inte varför man behöver sätta in i , och varför ska en derivata med avseende på x ha y som variabel?
, men varför behöver man ta steget att lägga in x = (y-2)^1/3?
Du hade ju redan beräknat dx/dy och uppgiften säger att du skall utnyttja detta för att lösa resten av uppgiften. Sedan är det väl lämpligt att uttrycka det i y så att man får df-1(y)/dy = någonting där y är variabeln. Sedan kan man byta namn på y till x för att få df-1(x)/dx.
Så ?
Vet inte exakt vad facit tänkt sig. Min gissning gavs i #3.
Annars hade jag nog startat från f(f-1(x)) = x och deriverat båda led samt utnyttjat kedjeregeln för att i slutändan få att
df-1(x)/dx = 1/f’(f-1(x)).
Men även i detta fall så måste man beräkna f-1(x) om man vill ha ett fullständigt svar, men då kan man väl lika gärna derivera f-1(x) direkt, så jag ser inte riktigt vad facit är ute efter.
Kan du visa facit?


