Sekant
Hej!
Jag har denna uppgift (1347)

Och har kommit så här långt på min lösning, men jag kommer ej fram till rätt svar. Samtidigt känns det som att min lösning är rimlig.

Uppskattar all hjälp!
Felet ligger i att du tar fram en viss information från en ekvation. Sedan använder du samma information i samma ekvation. Om du gjort rätt är det klart att likheten kommer gälla, men du har ju inte kommit någon vart. Du kan fundera på om svaret är rimligt? Vad händer om a är mindre än -4?
Visa spoiler
En annan metod är att hitta för vilka a linjen tangerar kurvan. Dessa kommer vara gränserna. Alla a mellan kommer ju resultera i sekanter. Rita upp i Desmos om du inte förstår vad jag menar.
Tillägg: 19 aug 2025 22:05
Glöm det i spoilern. Högst oklart vad jag tänkte att den graf såg ut som..
(Vad MrPotatohead skrev snabbare än undertecknad.)
Men rita är bra, tycker jag! Så jag gjorde det allra först, för att se problemet framför mig.
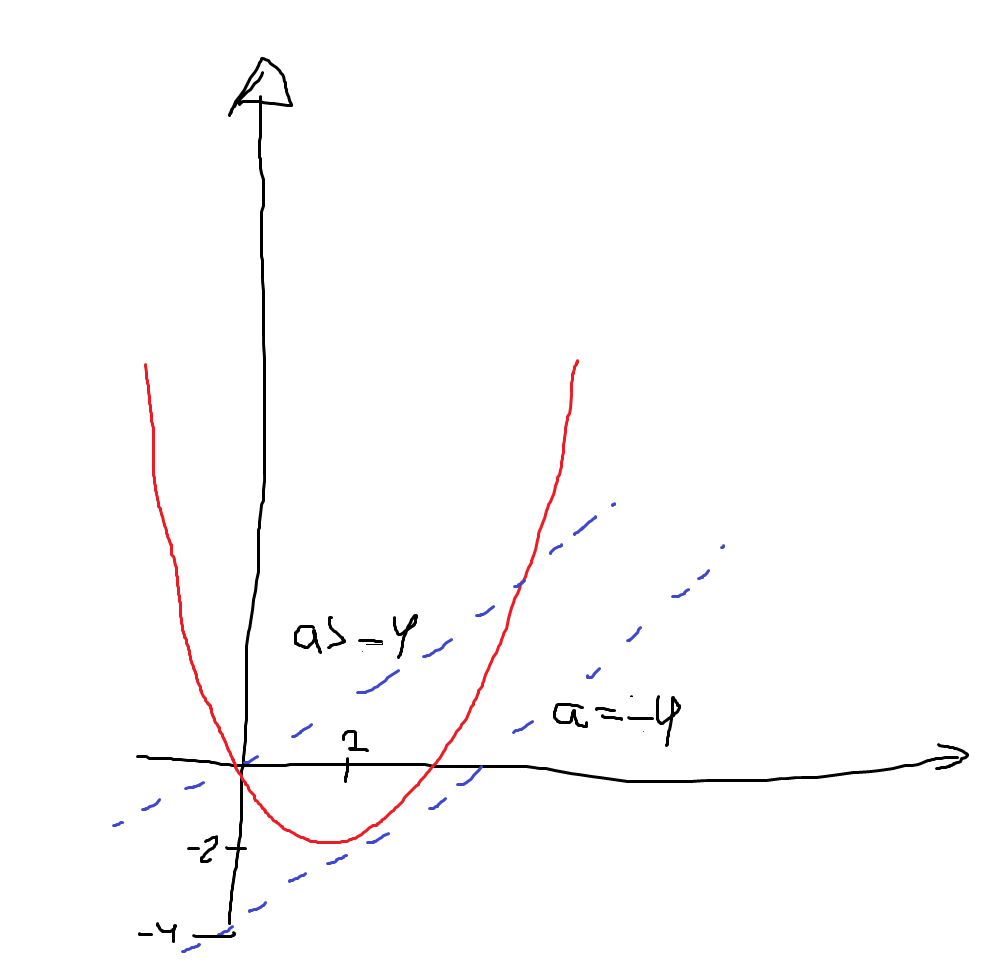
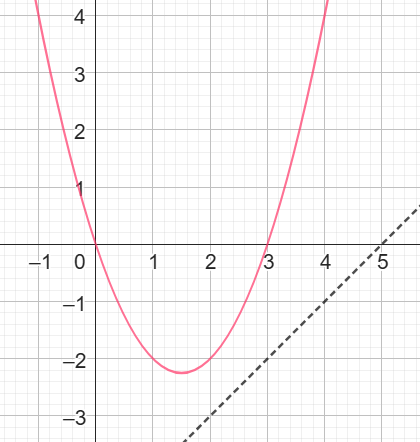
a=0 skär kurvan två gånger och ger oss en sekant:

a=-5 missar kurvan helt och sekant saknas:
Jag hänger med lite bättre nu. Men hur kan jag komma fram till detta algebraiskt?
Abcd1000 skrev:Jag hänger med lite bättre nu. Men hur kan jag komma fram till detta algebraiskt?
Hur vet man om en andragradsekvation, som den du ställde upp, har noll, en eller två reella lösningar?
Okej, så jag ska alltså använda mig av att disktiminanten måste vara positiv för att det ska finnas två lösningar till ekvationen eller alltså två skärningspunkter? Och jag vet att det endast finns två skärningspunkter eftersom det är en andragradsekvation???
Precis! När D>0 har du två skärningspunkter, en sekant, som vid a=0. När D=0 har du inte längre en sekant, utan en tangent. Vid D<0 har du ingenting, åtminstone inte i .
Okej, tycker du att detta duger eller ska jag också motivera hur jag vet att sekanten skär parabeln i två punkter?

Det går nog att lägga till någon kommentar om olikheten du ställt up där ja.
Jag tycker det är bra. Ännu tydligare skulle det vara om du drog några streck med en penna. Då kan man knappast missförstå hur du resonerar.
Kanske lite snyggare än mina 20 sekunder i MS Paint, men åt det hållet.
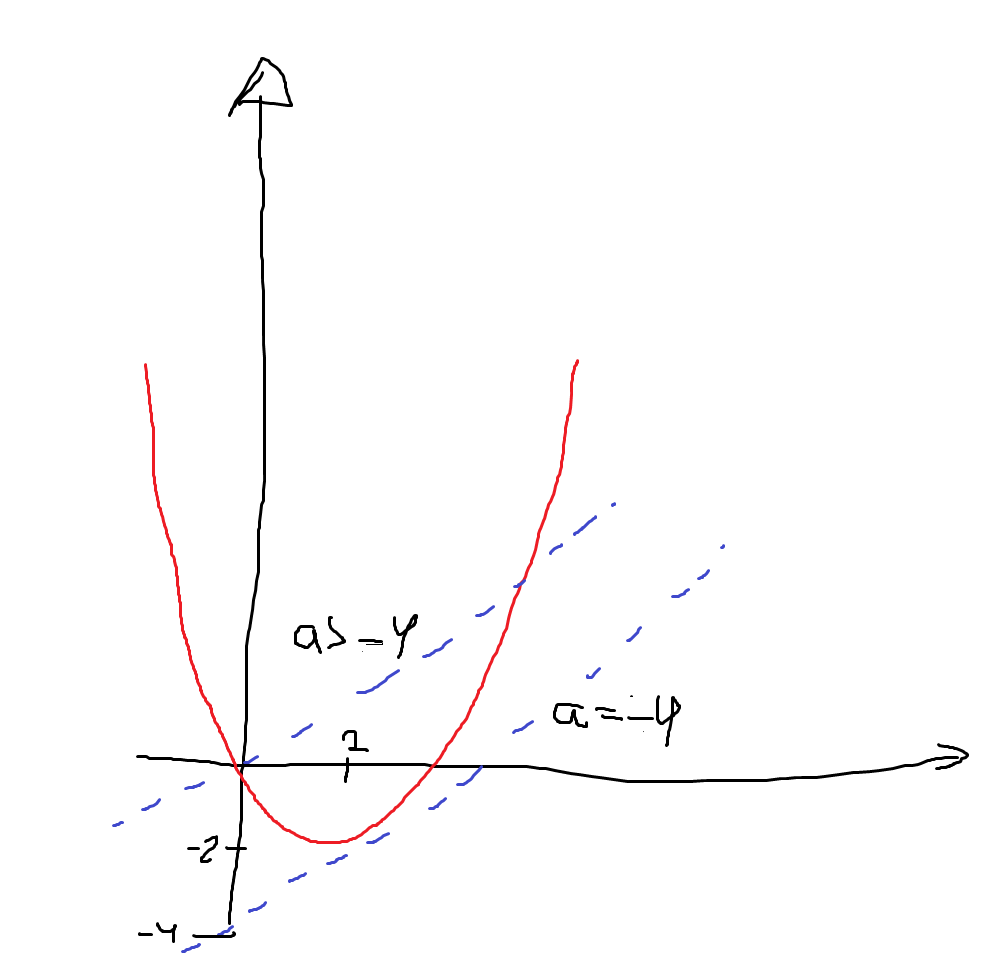
sictransit skrev:Jag tycker det är bra. Ännu tydligare skulle det vara om du drog några streck med en penna. Då kan man knappast missförstå hur du resonerar.
Kanske lite snyggare än mina 20 sekunder i MS Paint, men åt det hållet.
Bra idé, tack för hjälpen!
MrPotatohead skrev:Det går nog att lägga till någon kommentar om olikheten du ställt up där ja.
Vad tänker du på för kommentar?
Det är ganska uppenbart men något i stil med: "Ekvationen är bara definierad för a större eller lika med -4 och värden större än -4 ger två x-värden (sekant) a=-4 ger en ett x-värde (tangent)".