Sekularekvationen detB=0 (Matematik/Universitet)

Ekvationen

$Bv= 0$

Där B är en matris, v är en vektor och 0 är nollvektorn har alltid lösningen v = 0 (nollvektorn), den s.k triviala lösningen.

Om det(B) = 0 så finns det andra lösningsvektorer v till Bv = 0, s.k icketriviala lösningar. Hur lösningarna v ser ut får man då undersöka.

Dr. G skrev:
Ekvationen
$Bv= 0$
Där B är en matris, v är en vektor och 0 är nollvektorn har alltid lösningen v = 0 (nollvektorn), den s.k triviala lösningen.
Om det(B) = 0 så finns det andra lösningsvektorer v till Bv = 0, s.k icketriviala lösningar. Hur lösningarna v ser ut får man då undersöka.

Okej, men varför beräknar man just determinanten då?

Om det(B) ≠ 0 så är v = 0 den enda lösningen till Bv = 0.

Om det(B) = 0 så är v = 0 den enda lösningen till Bv = 0.

I ditt fall så blir det(B) = 0 för vissa värden på lambda. Sätt in det värdet och beräkna v ≠ 0 som löser ekvationen (s.k egenektorer till A med egenvärde lambda).

Determinanten heter som den gör just för att den bestämmer (engelska/latin determine) denna viktiga egenskap hos matrisen.

Hej!

Om matrisen $A-\lambda I$ är inverterbar så är vektorn $v=0$ den enda lösningen till det linjära ekvationssystemet $(A-\lambda I)v=0.$

Om matrisen inte är inverterbar kan det finnas flera lösningar ( $v$ ) till ekvationssystemet.

Det finns vissa speciella tal $\lambda$ som gör matrisen $A-\lambda I$ icke-inverterbar. Sådana tal är lösningar till polynomekvationen $\det(A-\lambda I)=0.$

Tack! man kan inte förklara varför den ger alla lösningar när vektorn v är olikt nollvektorn utan det gör determinanten bara eftersom det är dess egenskap? eller har jag missuppfattat det ni skrivit?

Ser att jag skrev fel ovan. Det skulle vara:

Om det(B) = 0 så är v = 0 INTE den enda lösningen till Bv = 0.

Om det(B) ≠ 0 så är v = 0 den enda lösningen till Bv = 0.

Dr. G skrev:
Ser att jag skrev fel ovan. Det skulle vara:
Om det(B) = 0 så är v = 0 INTE den enda lösningen till Bv = 0.
Om det(B) ≠ 0 så är v = 0 den enda lösningen till Bv = 0.

Tänkte det, men bara för att determinanten är 0 borde väll inte ekvationen $(A - λ I) * \overset{⇀}{v} = \overset{⇀}{0}$

uppfyllas?

När det gäller determinanter gillar jag att tänka geometriskt.

En matris $B$ representerar ju en linjär avbildning som tar in en vektor $v$ och spottar ut en annan vektor $Bv$ . Geometriskt sett kan vi se detta som att alla punker i rummet förflyttas till en annan punkt. Determinanten anger hur mycket rummet förminskas eller förstoras när denna förflyttning sker. Om vi till exempel har en parallellogram i $\mathbb{R}^2$ med arean $1\ \text{a.e.}$ som spänns upp av två vektorer kommer parallellogramen som spänns upp av vektorerna efter de förflyttats genom en linjär avbildning med determinanten $3$ att förstoras tre gånger, d.v.s. den nya arean blir $3\ \text{a.e}$ .

Vad betyder det då att determinanten är lika med noll? Jo, det betyder att rummet förminskas så mycket att det får en annan dimension. Till exempel kan en linjär avbildning ta in vektorer i hela tredimensionella $\mathbb{R}^3$ men bara spotta ut vektorer i ett tvådimensionellt plan. Då har rummets dimension minskat från tre till två, och då kommer determinanten att vara noll.

(Determinanten kan även vara negativ, men det är egentligen samma sak som att den är positiv, bara att man byter mellan högerorienterat och vänsterorienterat system)

När vi studerar en ekvation av typen $Ax=b$ frågar vi oss i detta sammanhang "vilka vektorer $x$ förflyttas till $b$ efter transformation med matrisen $A$ ?". Om determinanten är nollskild kommer varje vektor $x$ förflyttas till en unik plats i rummet eftersom rummet fortfarande är tredimensionellt. Då finns det bara en lösningen till ekvationen $Ax=b$ . Är determinanten däremot lika med noll kommer att rummet att 'tryckas ihop' och flera vektorer kommer att hamna på samma plats. Då kan det finnas flera lösningar till ekvationen $Ax=b$ .

AlvinB skrev:
När det gäller determinanter gillar jag att tänka geometriskt.
En matris $B$ representerar ju en linjär avbildning som tar in en vektor $v$ och spottar ut en annan vektor $Bv$ . Geometriskt sett kan vi se detta som att alla punker i rummet förflyttas till en annan punkt. Determinanten anger hur mycket rummet förminskas eller förstoras när denna förflyttning sker. Om vi till exempel har en parallellogram i $\mathbb{R}^2$ med arean $1\ \text{a.e.}$ som spänns upp av två vektorer kommer parallellogramen som spänns upp av vektorerna efter de förflyttats genom en linjär avbildning med determinanten $3$ att förstoras tre gånger, d.v.s. den nya arean blir $3\ \text{a.e}$ .
Vad betyder det då att determinanten är lika med noll? Jo, det betyder att rummet förminskas så mycket att det får en annan dimension. Till exempel kan en linjär avbildning ta in vektorer i hela tredimensionella $\mathbb{R}^3$ men bara spotta ut vektorer i ett tvådimensionellt plan. Då har rummets dimension minskat från tre till två, och då kommer determinanten att vara noll.
(Determinanten kan även vara negativ, men det är egentligen samma sak som att den är positiv, bara att man byter mellan högerorienterat och vänsterorienterat system)
När vi studerar en ekvation av typen $Ax=b$ frågar vi oss i detta sammanhang "vilka vektorer $x$ förflyttas till $b$ efter transformation med matrisen $A$ ?". Om determinanten är nollskild kommer varje vektor $x$ förflyttas till en unik plats i rummet eftersom rummet fortfarande är tredimensionellt. Då finns det bara en lösningen till ekvationen $Ax=b$ . Är determinanten däremot lika med noll kommer att rummet att 'tryckas ihop' och flera vektorer kommer att hamna på samma plats. Då kan det finnas flera lösningar till ekvationen $Ax=b$ .

Tack! vet inte om jag uppfattat det rätt men kan man säga att genom att sätta det(B)= 0 får man lösningar i andra dimensioner än i den dimension som A- $λ$ I är i?

Till Lamayo. Objektet $A-\lambda I$ är en matris med $n$ rader och $m$ kolonner så "dimensionen" som du refererar till är $n\times m$ eller är det någon annan dimension du avser?

Albiki skrev:
Till Lamayo. Objektet $A-\lambda I$ är en matris med $n$ rader och $m$ kolonner så "dimensionen" som du refererar till är $n\times m$ eller är det någon annan dimension du avser?

Förstår tyvärr inte. Jag tänkte att om man räknade ut det(B)=0 så fick man lösningar i en annan dimension, men känner mig ganska förvirrad :/

Albiki skrev:
Hej!
Om matrisen $A-\lambda I$ är inverterbar så är vektorn $v=0$ den enda lösningen till det linjära ekvationssystemet $(A-\lambda I)v=0.$
Om matrisen inte är inverterbar kan det finnas flera lösningar ( $v$ ) till ekvationssystemet.
Det finns vissa speciella tal $\lambda$ som gör matrisen $A-\lambda I$ icke-inverterbar. Sådana tal är lösningar till polynomekvationen $\det(A-\lambda I)=0.$

Till Lamayo. Läs mitt citerade inlägg en gång till och försök förstå det jag skriver. Fråga om något jag skrev är otydligt.

Jag kanske ska ta ett exempel och rita lite för att försöka förtydliga vad jag menar.

Om vi har en linjär avbildning vars matris har en nollskild determinant kommer dimensionen på vektorrummet som utgör definitionsmängden vara samma som dimensionen på vektorrummet som utgör värdemängden. Då trycks rummet inte ihop under transformationen, och varje 'invektor' får en unik 'utvektor'. Låt oss ta ett exempel i $\mathbb{R}^2$ . Här har jag ritat upp ett antal vektorer och deras lägen före och efter avbildning:

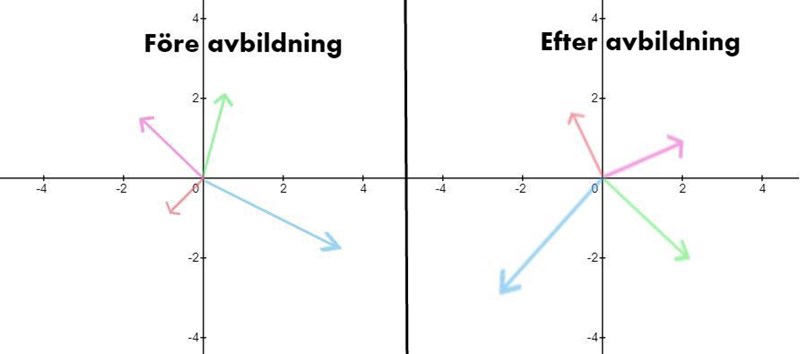
Eftersom determinanten är nollskild kommer dimensionen på definitionsmängden ( $2$ , vi arbetar ju i $\mathbb{R}^2$ ) att vara lika med dimensionen på värdemängden (också $2$ ). Detta ser vi eftersom vektorerna vi får ut kan vara var som helst i hela $\mathbb{R}^2$ . Då får varje vektor till vänster en unik plats till höger. Detta gör att en ekvation $Ax=b$ endast har en lösning.

Om determinanten däremot är lika med noll kommer värdemängdens dimension att vara lägre än definitionsmängdens. Låt oss än en gång ta ett exempel i $\mathbb{R}^2$ :

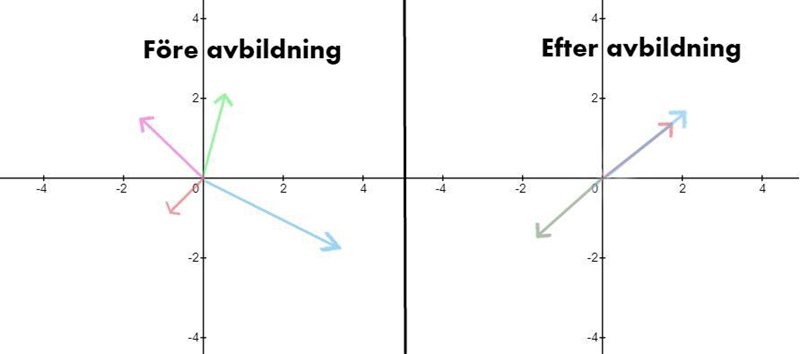
Här ser vi att vektorerna hamnar på enda linje (som ju har dimension ett!). Vi började ju med vektorer i ett tvådimensionellt plan ( $\mathbb{R}^2$ ), men slutade med vektorer på en endimensionell linje! Eftersom vi nu har tryckt ihop rummet kommer flera 'invektorer' att hamna på samma 'utvektor'. Detta har jag försökt illustrera genom att den lila och den gröna vektorn är på samma plats till höger (men det syns tyvärr inte så bra...). Eftersom vi nu har att flera vektorer hamnar på samma ställe efter transformationen kan det finnas flera $x$ som hamnar på vektorn $b$ , och alltså kan ekvationen $Ax=b$ ha flera lösningar ifall determinanten är lika med noll.

I vårt fall ser vi att ekvationen $Bv=0$ endast har en lösning om $\det(B)\neq0$ eftersom det då endast finns en vektor $v$ som hamnar på nollvektorn, men om $\det(B)=0$ finns det flera vektorer $v$ som hamnar på nollvektorn och då har vi flera lösningar till $Bv=0$ .

Det är alltså ett nödvändigt villkor att $\det(B)=0$ för att kunna hitta andra lösningar än $v=0$ till ekvationen $Bv=0$ .

Till Lamayo.

Varje eventuell lösning tiil ekvationssystemet $Av=b$ kan skrivas som

$v=x+u$

där $u$ är en lösning till systemet $Au=0$ och x är en lösning till systemet $Ax=b$ .

Om matrisen $A$ är inverterbar är $u=0$ den enda lösningen till $Au=0$ ; man säger att nollrummet till matrisen A innehåller endast nollvektorn.
Om matrisen $A$ inte är inverterbar innehåller nollrummet till $A$ oändligt många vektorer ( $u$ ) och var och en av dessa motsvarar en lösning till systemet $Av=b$ enligt ovan.

Tack så mycket för all hjälp, nu fattar jag! :)