Separation av variabler
Jag har lyckats lösa denna uppgift korrekt när det gäller y-delen.

Men när vi kommer till x-delen förstår jag inte riktigt vad facit gör, speciellt i bilden nedan. Det är ju en andra ordningens homogen ODE, som jag är van vid att lösa med karaktäristiska ekvationen där jag beräknar r, och om r blir två olika reella tal (vilket det blir i detta fall) så borde X(x) vara lika med An*e^rx + Bn*e^-rx, så jag förstår inte vart cosh nx och sinh nx kommer ifrån?
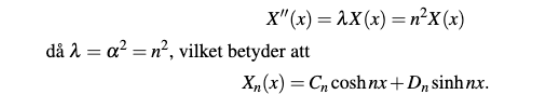
A * e^rx + B * e^-rx
Kan man skriva om till
C1 * (e^rx + e^-rx) + C2 * (e^rx - e^-rx)
vad har det md cosh nx och sinh nx att göra? Och varför ska man ens skriva om till hyperboliska funktioner?
Du kan använda exponentialfunktionen eller hyperboliska funktioner. Valfritt! Testa båda och se vilket som ger trevligaste svaret.
Jag antar att n kommer från din lösning av ”y-delen”. Du har säkert fått att randvillkoren på ”y-delen” endast kan uppfyllas om , där n är ett heltal.


