Sinus

Det låter som en bra början.

Kanske en liten substitution skulle sitta fint efter det.

Det går att göra en substitution men finns även ett annat sätt att se vad lösningarna är.

Det står ange samtliga lösningar, syftar de på på grundekvationerna för sin cos?

fastnat igen:

Du har gjort rätt hittills. Efter att du har faktoriserat kan du använda dig av nollproduktsmetoden för att komma vidare.

Om x=0 så är sin0=0
Så blir det +1 inom parentesen?

Nollproduktsmetod handlar om att kolla när varje faktor är lika med noll. I det här fallet har du två faktorer, sin(x) och sin(x) + 1. Du behöver lösa ut när dessa är lika med noll vilket ger två ekvationer som måste lösas.

X₁=0 och x₂=-1

två ekvationer såsom sinus grundekvation?

Vi kan sätta båda faktorerna lika med noll för att ta reda på när de är lika med noll och därav när hela ekvationen är noll. Då får vi att 

sin(x) = 0 och sin(x) + 1 = 0.

Sen löser vi ut vad x är ur båda ekvationerna.

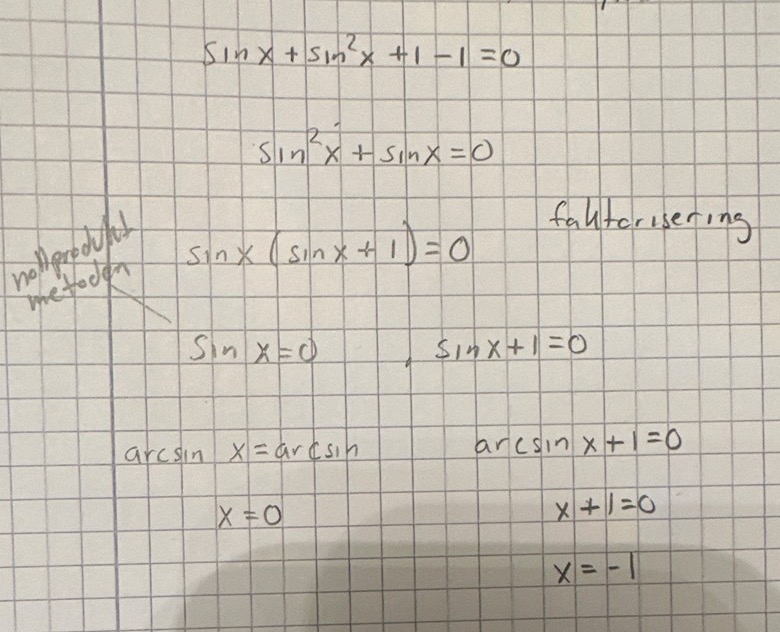
såhär? Sedan?

sin(x) = 0 är ju ganska enkel att lösa eftersom sin(x) är lika med noll vid 0 och 180 grader, sen kan du addera eller subtrahera perioder för att få resten av lösningarna.

sin(x) + 1 = 0 löser vi genom att lösa ut sin(x), då får vi sin(x) = -1. sin(x) = -1 vid 270 grader, sedan kan du addera eller subtrahera perioder för att få resten av lösningarna.

Man kan hänvisa till enhetscirkeln och rita upp en bild som visar att sin(0 grader) = sin(180 grader) = 0 och sin(270 grader) = -1.

Såhär?

Biorr skrev:

[...]

Såhär?

[...]

Nej, det blev fel på några ställen, se bild:

• A: Ofullständig ekvation.
• B: Här tar du arcsin(x+1), vilket du inte ska göra. Därför blir x₃ fel.
• C: Här blandar du grader och radianer.
• D: Här har du bytt från x₃ = -1 till x₃ = -3pi/4+n•2pi (som inte heller är några lölösningar).

=======

Tips:

Skriv istället så här:

$\sin(x)+1=\cos^2(x)$

Trigettan i VL:

$\sin(x)+\sin^2(x)+\cos^2(x)=\cos^2(x)$

Förenkla:

$\sin^2(x)+\sin(x)=0$

Faktorisera:

$\sin(x)(\sin(x)+1)=0$

Nollproduktmetoden ger nu de två ekvationerna

1. $\sin(x)=0$
2. $\sin(x)+1=0$, dvs $\sin(x)=-1$

Ekvation 1: 

$x=\arcsin(0)+n\cdot360^{\circ}$ och $x=180^{\circ}-\arcsin(0)+n\cdot360^{\circ}$

$x=0^{\circ}+n\cdot360^{\circ}$ och $x=180^{\circ}-0^{\circ}+n\cdot360^{\circ}$

Förenklat: $x=n\cdot180^{\circ}$

Ekvation 2:

$x=\arcsin(-1)+n\cdot360^{\circ}$ och $x=180^{\circ}-\arcsin(-1)+n\cdot360^{\circ}$

$x=-90^{\circ}+n\cdot360^{\circ}$ och $x=180^{\circ}-(-90^{\circ})+n\cdot360^{\circ}$

$x=-90^{\circ}+n\cdot360^{\circ}$ och $x=270^{\circ}+n\cdot360^{\circ}$

Förenklat: $x=-90^{\circ}+n\cdot360^{\circ}$

=====

Välj nu de värden på heltalet $n$ som ger lösningar i det önskade intervallet.