Sinus

En bild säger mer än tusen ord, är ett gammalt talesätt. Har du möjlighet att posta en sådan?

sictransit skrev:

En bild säger mer än tusen ord, är ett gammalt talesätt. Har du möjlighet att posta en sådan?

"Det står 32 grader"

ABC1 skrev:

sictransit skrev:

En bild säger mer än tusen ord, är ett gammalt talesätt. Har du möjlighet att posta en sådan?

"Det står 32 grader"

Har till och med frågat chatGPT och dess förklaring gör mig ännu mer förvirrad. Fattar inte vad författarna såg för att lägga det som lösning

Ja, det var ju en märklig uppgift. Det håller jag med om.

Eftersom vi har kateterna på den vänstra kan vi räkna ut hypotenusan med pythagoras:

$\sqrt{0,{75}^2+1,2^2}\approx 1,42$

Trianglarna har lika vinklar, vilket ger att det är likformiga:

$\frac{1,2}{\sqrt{0,{75}^2+1,2^2}}=\frac{x}{0,75}\Rightarrow x\approx 0,64 \mathrm{m}$

Se där! Ingen trigonometri alls, utan högstadiematte.

Sedan har du ju mycket riktigt konstaterat att man kan använda cosinus eftersom vi har vinkeln. Cosinus är ju närliggande genom hypotenusan:

$\cos (32°)=\frac{x}{0,75}\Rightarrow x\approx 0,64 \mathrm{m}$

Det blir förstås samma resultat, åtminstone om man avrundar lite. Vinkeln är inte precis 32 grader, vilket vi kan visa genom att använda tangens på den vänstra.

sictransit skrev:

Ja, det var ju en märklig uppgift. Det håller jag med om.

Eftersom vi har kateterna på den vänstra kan vi räkna ut hypotenusan med pythagoras:

$\sqrt{0,{75}^2+1,2^2}\approx 1,42$

Trianglarna har lika vinklar, vilket ger att det är likformiga:

$\frac{1,2}{\sqrt{0,{75}^2+1,2^2}}=\frac{x}{0,75}\Rightarrow x\approx 0,64 \mathrm{m}$

Se där! Ingen trigonometri alls, utan högstadiematte.

Sedan har du ju mycket riktigt konstaterat att man kan använda cosinus eftersom vi har vinkeln. Cosinus är ju närliggande genom hypotenusan:

$\cos (32°)=\frac{x}{0,75}\Rightarrow x\approx 0,64 \mathrm{m}$

Det blir förstås samma resultat, åtminstone om man avrundar lite. Vinkeln är inte precis 32 grader, vilket vi kan visa genom att använda tangens på den vänstra.

Själva uppgiften handlade inte enbart om detta utan det handlade om kraftmoment inom fysiken men en enskild deluppgift inkluderade att räkna ut x men förstår fortfarande inte hur sin(32) * 1,2 blir samma svar som 0.75 * cos(32) 

Det råkar vara så att de är lika vid nästan precis 32 grader. Klurig uppgiftskonstruktör, eller ren slump.

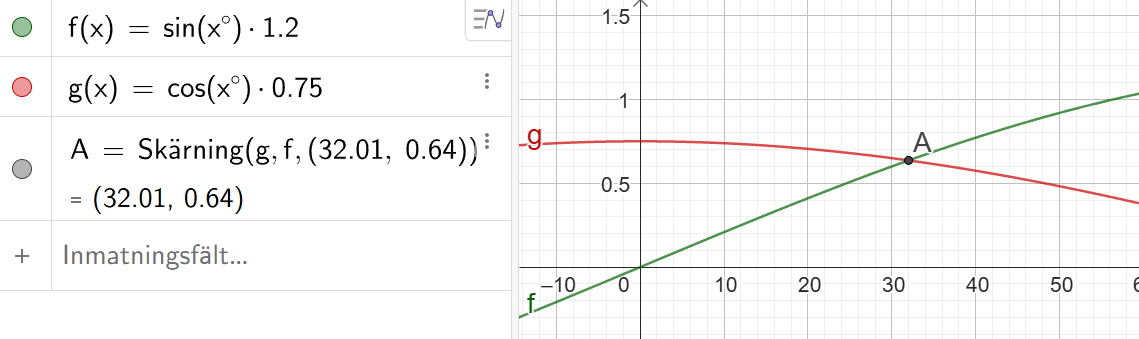
tack, blev lite för förvirrad

ABC1 skrev:

sictransit skrev:

 

Själva uppgiften handlade inte enbart om detta utan det handlade om kraftmoment inom fysiken men en enskild deluppgift inkluderade att räkna ut x men förstår fortfarande inte hur sin(32) * 1,2 blir samma svar som 0.75 * cos(32) 

om du kallar hypotenusan i den stora triangeln för y så har vi: (för en rätvinklig triangel gäller att sin(vinkel) = motstående katet/hypotenusa och cos(vinkel) = närstående katet/hypotenusa)

1.  0,75 = y*sin(32) => y = 0,75/sin(32)

och 

2.  1,2 = y*cos(32) => y = 1,2/cos(32)

Vill vi sen beräkna x har vi likformighet som ger att

x= 0,75*1,2/y

vilket ger dessa 2 uttryck för x

1.  [ y = 0,75/sin(32) ] =>  x = 1,2*sin(32)

2. [ y = 1,2/cos(32)  ] => x = 0,75*cos(32)