Ska man sätta in värderna på formeln?
Hej! Jag behöver hjälp med b) frågan
av a) fick vi värdena 2,3,7,43
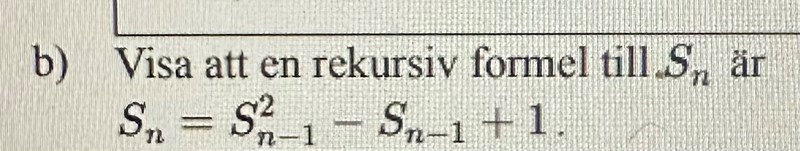
ska man då på b) lägga först n =1 för att se om den gäller för s0.
när jag testade fick jag ut svaret 3 som man fick ut på a)
är detta rätt tankesätt? Eller löser man denna frågan på ett annat sätt?
Har ni lärt er induktion?
Ja det är väl summa symbol och formel ?
AlexMu skrev:Har ni lärt er induktion?
Jag tror det är direkt insättning bara som skall användas.
Vi har, per definition, att
S_n = ∏_0^{n-1} S_i + 1 = S_{n-1} * ∏_0^{n-2} S_i + 1
S_{n-1} = ∏_0^{n-2} S_i + 1, dvs. ∏_0^{n-2} S_i = S_{n-1}-1 som sätts in i ovan;
S_n = S_{n-1} (S_{n-1}-1) + 1 = S_{n-1}^2 - S_{n-1} + 1.
V.s.v.
Ah! Det missade jag. Snyggt.
Trinity2 skrev:AlexMu skrev:Har ni lärt er induktion?
Jag tror det är direkt insättning bara som skall användas.
Vi har, per definition, att
S_n = ∏_0^{n-1} S_i + 1 = S_{n-1} * ∏_0^{n-2} S_i + 1
S_{n-1} = ∏_0^{n-2} S_i + 1, dvs. ∏_0^{n-2} S_i = S_{n-1}-1 som sätts in i ovan;
S_n = S_{n-1} (S_{n-1}-1) + 1 = S_{n-1}^2 - S_{n-1} + 1.
V.s.v.
Jag förstår inte symbolerna men är det som jag föreslog ? Att lägga värdena från a) och sätta in de i formeln på b)
Inte värdena. Du ska visa det för alla n, så sätt in uttrycket för Sn (och Sn-1).
