Skärningspunkter mellan en andragradsfunktion och en linjär funktion

hej! Jag vet verkligen inte var jag ska börja med denna fråga:

För två funktioner f och g gäller att y=f(x) och y=g(x). Vilka värden kan riktningskoefficienten k ha för att graferna till funktionerna f(x)=x^2+4 och g(x)=kx+2 ska skära varandra två gånger?

allt jag kom fram till var att f(x) har sin extrempunkt vid (0,4) och att g(x) skär y-axeln vid 2. Jag försökte experimentera med ett grafiterade hjälpmedel för att hitta ett mönster för värden på K där det finns två skärningspunkter, men kom inte fram till något. Sedan försökte jag bryta ut vad k skulle vara när funktionerna är lika med varandra:

$x^{2} + 4 = k x + 2 x^{2} + k x = - 2 x (x - k) = - 2 e f t e r s o m x k a n v a r a b å d e p o s i s t i v t o c h n e g a t i v t f å r j a g g ö r a t v å o l i k a l ö s n i n g a r : x - k = \frac{- 2}{x} k = x + \frac{2}{x} x - k = \frac{- 2}{- x} = \frac{2}{x} k = x - \frac{2}{x}$

men detta säger mig inget. Hur ska jag tänka med frågor som dessa?

om du löser ekvationen

x²+kx=−2 med pq formeln får du,

x² +kx +2 = 0

$x = - k / 2 \pm \sqrt{{(\frac{k}{2})}^{2} - 2}$

För att du ska få två lösningar på denna måste uttrycket under rottecknet vara > 0

om den = 0 får vi bara en lösning
om den < 0 för vi inga reella lösningar

För vilka värden på k blir uttrycket under rottecknet > = 0 ?

ahaaa smart!

$\sqrt{\frac{k^{2}}{4} - 2} \geq 0 j a g k v a d r e r a r b å d a l e d e n \frac{k^{2}}{4} - 2 \geq 0 \frac{k^{2}}{4} - 2 \leq 0 \frac{k^{2}}{4} \geq 2 k^{2} \geq 8 \sqrt{k^{2}} \geq \sqrt{8} k \geq \sqrt{8} k \leq \sqrt{8}$

tack för hjälpen!!

har du provat dina lösningar? (jag antar att du missade ett minustecken på slutet! )

är verkligen $\pm \sqrt{8}$

tillåtna värden?

nej det glömde jag, bra att du påminde! men ja, båda lösningarna fungerar!

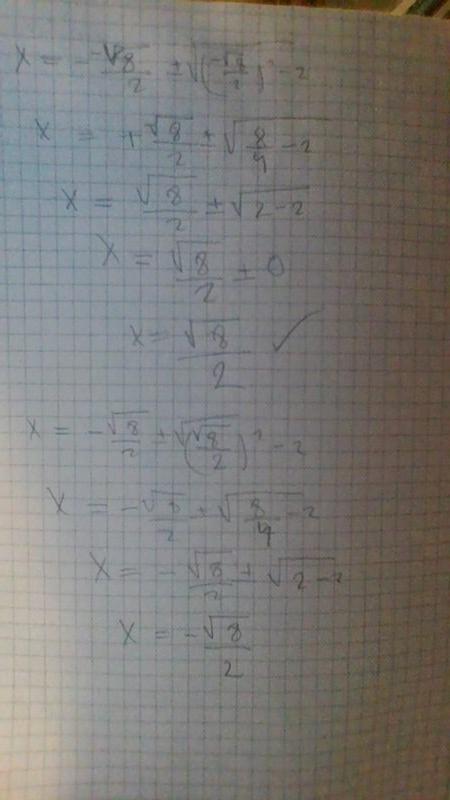
Med k = roten ur 8 blr värdet under roten 0 och vi har bara en lösning på x

så k ska vara strikt större än roten ur 8

eller strikt mindre än - roten ur 8

likhet är ej tillåtet värde

Ture skrev:
Med k = roten ur 8 blr värdet under roten 0 och vi har bara en lösning på x

så k ska vara strikt större än roten ur 8

eller strikt mindre än - roten ur 8

likhet är ej tillåtet värde

Ja, vet att det blev fel tecken men hittade inte det för strikt olikhet på datorn!

Svara Avbryt

Visa senaste svar