Skillnaden mellan ytintegral och flödesintegral.


Där använder man att normalen |N|=3.
men när man kollar på flödesintegralens normal:
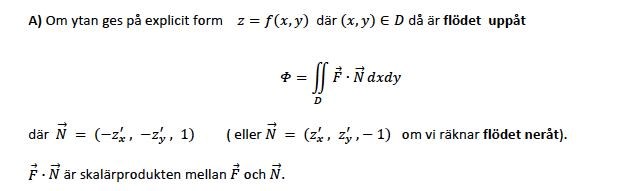
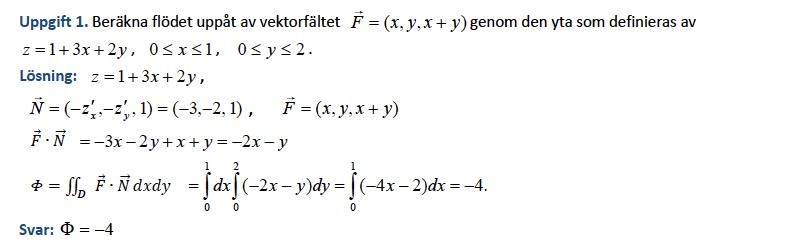
Varför gör man det olika?
Man gör det olika för att en ytintegral och en flödesintegral är olika saker. Ytan (och därmed normalvektorn) råkar vara densamma men i ytintegralen används normalvektorns absolutbelopp och i flödesintegralen används skalärprodukten mellan ett vektorfält och normalvektorn.
Detaljerna kring varför har med definitionen av integraltyperna att göra.
Ebola skrev:Man gör det olika för att en ytintegral och en flödesintegral är olika saker. Ytan (och därmed normalvektorn) råkar vara densamma men i ytintegralen används normalvektorns absolutbelopp och i flödesintegralen används skalärprodukten mellan ett vektorfält och normalvektorn.
Detaljerna kring varför har med definitionen av integraltyperna att göra.
Okej, men hur skulle man veta - tex på en tenta- vad som är vad?
mrlill_ludde skrev:Ebola skrev:Man gör det olika för att en ytintegral och en flödesintegral är olika saker. Ytan (och därmed normalvektorn) råkar vara densamma men i ytintegralen används normalvektorns absolutbelopp och i flödesintegralen används skalärprodukten mellan ett vektorfält och normalvektorn.
Detaljerna kring varför har med definitionen av integraltyperna att göra.
Okej, men hur skulle man veta - tex på en tenta- vad som är vad?
Jag förstår inte din fråga. Om uppgiften ber dig beräkna en flödesintegral så gör du det, vice versa för en ytintegral? Att beräkna dem är bara formler och definitioner vilket gör det uppenbart vad som är vad. Är det något jag missat med din fråga?
Ebola skrev:mrlill_ludde skrev:Ebola skrev:Man gör det olika för att en ytintegral och en flödesintegral är olika saker. Ytan (och därmed normalvektorn) råkar vara densamma men i ytintegralen används normalvektorns absolutbelopp och i flödesintegralen används skalärprodukten mellan ett vektorfält och normalvektorn.
Detaljerna kring varför har med definitionen av integraltyperna att göra.
Okej, men hur skulle man veta - tex på en tenta- vad som är vad?
Jag förstår inte din fråga. Om uppgiften ber dig beräkna en flödesintegral så gör du det, vice versa för en ytintegral? Att beräkna dem är bara formler och definitioner vilket gör det uppenbart vad som är vad. Är det något jag missat med din fråga?
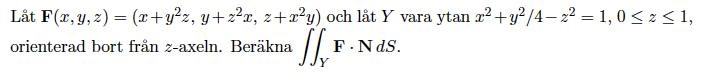
här, är deth är en flödes eller en ytinegraL?
Det här är en flödesintegral eftersom du integrerar i ett vektorfält. Det syns tydligt på skalärprodukten .
I en ytintegral integrerar man i ett skalärfält. Då har man bara en funktion som integrand.
Det är en flödesintegral. Du ser att du har skalärprodukt mellan ett vektorfält F och en normalvektor N. Det du gör är att du integrerar över ytan och summerar alla komponenter av vektorfältet som är normala till ytan.
Jämför med att du har ett rör och vill beräkna flödet av någon gas igenom ett tvärsnitt. Då kan du beskriva en flödesintegral som beräknar detta åt dig.
AlvinB skrev:Det här är en flödesintegral eftersom du integrerar i ett vektorfält. Det syns tydligt på skalärprodukten .
I en ytintegral integrerar man i ett skalärfält. Då har man bara en funktion som integrand.
jahaaa okej, så allt med skalärar är flödesintegraler :-)
Ebola skrev:Det är en flödesintegral. Du ser att du har skalärprodukt mellan ett vektorfält F och en normalvektor N. Det du gör är att du integrerar över ytan och summerar alla komponenter av vektorfältet som är normala till ytan.
Jämför med att du har ett rör och vill beräkna flödet av någon gas igenom ett tvärsnitt. Då kan du beskriva en flödesintegral som beräknar detta åt dig.

är detta flödes eller ytintegral?
AlvinB skrev:Det här är en flödesintegral eftersom du integrerar i ett vektorfält. Det syns tydligt på skalärprodukten .
I en ytintegral integrerar man i ett skalärfält. Då har man bara en funktion som integrand.
se mitt inlägg ovan :-)
Det där är en linjeintegral på en viss kurva gamma, möjligtvis kan man strukturera den så att Stokes sats kan användas. Det känns som att du borde läsa i boken eller gå igenom föreläsningsanteckningar.
Ebola skrev:Det där är en linjeintegral på en viss kurva gamma, möjligtvis kan man strukturera den så att Stokes sats kan användas. Det känns som att du borde läsa i boken eller gå igenom föreläsningsanteckningar.
Det är Stokes sats, men eftersom man har med Normalen N här i rot F * N
så undrar jag vilken N är det använder?
Du kan läsa om det här:
http://www.sth.kth.se/armin/ALLA_KURSER/SF1626/STOKES.pdf
Eller se här:

Normalen är orienterad enligt högerhandsregeln där fingrarna följer kurvan och tummen följer normalvektorns riktning.
Ebola skrev:Du kan läsa om det här:
http://www.sth.kth.se/armin/ALLA_KURSER/SF1626/STOKES.pdf
Eller se här:
Normalen är orienterad enligt högerhandsregeln där fingrarna följer kurvan och tummen följer normalvektorns riktning.
Mjaa..
Men vilket N är det man använder i Stokes?
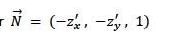
eller
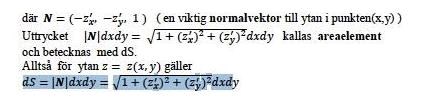
mrlill_ludde skrev:Ebola skrev:Du kan läsa om det här:
http://www.sth.kth.se/armin/ALLA_KURSER/SF1626/STOKES.pdf
Eller se här:
Normalen är orienterad enligt högerhandsregeln där fingrarna följer kurvan och tummen följer normalvektorns riktning.
Mjaa..
Men vilket N är det man använder i Stokes?
eller
Vad är det du frågar exakt? Det där är samma normalvektor N i båda bilder. Det känns som att du undrar något mer fundamentalt vilket är varför jag tycker du bör läsa föreläsningsanteckningar/boken eller kolla på Khan Academy.
MIT open source på Multi-variable calculus är också bra.



