Skiss med hjälp av derivata
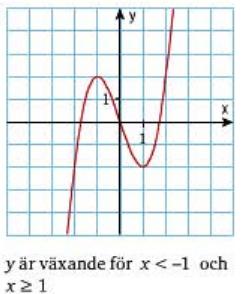
Kurvan växer då x<-1 stämmer, men varför står det x≥1, borde det inte stå x>0 ?
Nej, det borde stå att funktionen är växande i intervallet och i intervallet .
Detta enligt följande definition på växande funktion.
Varför tycker du att det borde stå x > 0?
Skrev fel menade en x>1 och inte noll. Men det borde stå x<-1 och x>1, pga att då värdet är 1 eller -1 då är lutningen noll, alltså växer/minskar inget. Eller?
Hur definieras "ökande" i matematik?
aha jag tror jag fattar vad ni menar nu. Alltså att det går från ett lägre värde till ett högre, alltså om man skulle rita ut derivatan av det här så skulle det gå från t.ex. -1 till 0 och det är en ökning, eller? Och då borde det väl stå som Yngve skrev från början x≤−1, x≥1 och inte x<-1 och x≥1 som det gör i boken?
Arbetsmyran skrev:aha jag tror jag fattar vad ni menar nu. Alltså att det går från ett lägre värde till ett högre, alltså om man skulle rita ut derivatan av det här så skulle det gå från t.ex. -1 till 0 och det är en ökning, eller?
Jag förstår inte riktigt vad du menar med "derivatan av det här". Om du ritar derivatan till grafen i bilden så kommer den att vara
- > 0 för alla x < -1
- = 0 för x = -1
- < 0 för -1 < x < 1
- = 0 för x = 1
- > 0 för x > 1
På grafen ser det ut som om derivatan avtar för x < 0 och ökar för x > 0, så det har inget att göra med huruvida funktionen är ökande eller inte.
Och då borde det väl stå som Yngve skrev från början x≤−1, x≥1 och inte x<-1 och x≥1 som det gör i boken?
Ja, det är så jag tolkar definitionen, att både x = -1 och x = 1 ingår i respektive intervall för vilka funktionen är växande.




