Skivmetoden för icke cirkulära skivor.
Hej,
Jag undrar om någon har en bra sida/video för detta eller om någon kan förklara. Har en sida i boken här som tar upp det men jag förstår ingenting utav det. Är det ens en rotationsvolym eller två funktioner i två plan eller ja.. vadå.
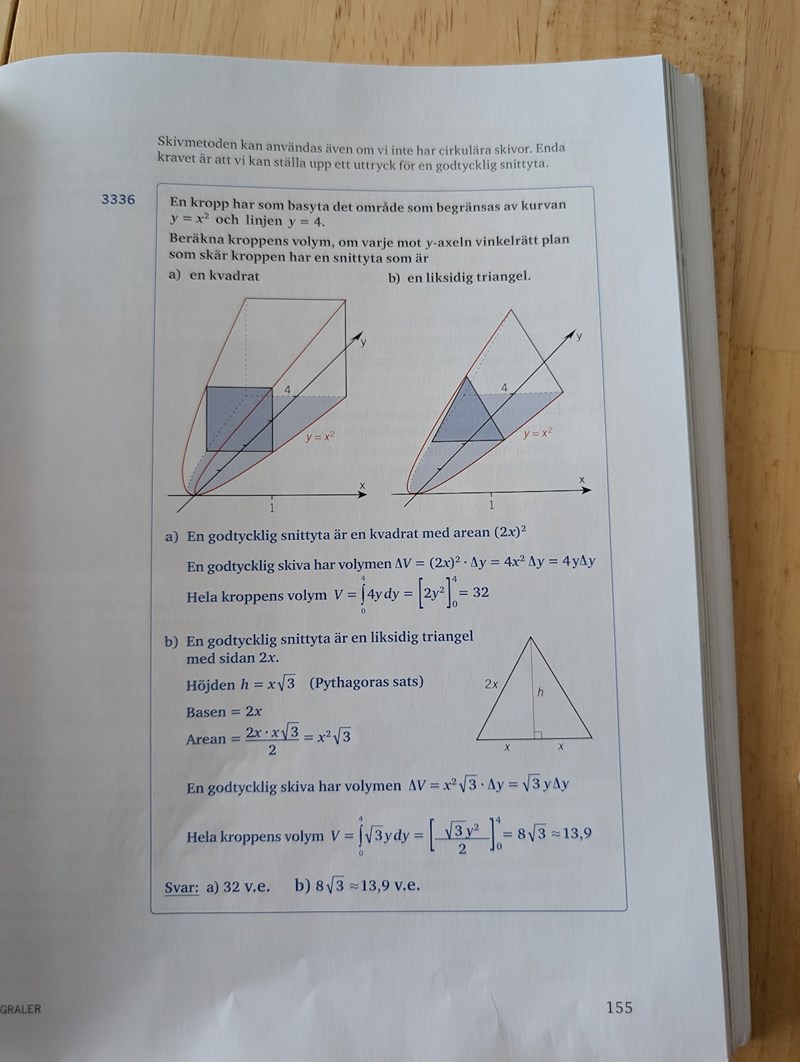
Hej,
Jag tycker att figurernas färgsättning förvirrar, så att man lockas tro att funktionen som är skriven i rött, y=x^2, drar iväg i ytterligare en dimension. Det gör funktionskurvan såklart inte.
Tänk dig istället det vanliga x-y-planet som du är van vid, och funktionskurvan y=x^2.
Men istället för att låta kurvan rotera,, med y-axeln som rotations axel, och därmed skapa en volym med cirkulär snittyta, så skapar man istället en kvadratisk snittyta, där kvadratens sida består av avståndet parallellt med x-axeln som stängs inne av funktionskurvan y=x^2.
(Kanske låter lika förvirrat som bokens beskrivning...)
Principen är att du tar fram ett uttryck för arean av en skiva som är vinkelrät mot integrationsriktningen. Skivorna behöver alltså inte vara cirkulära.
Vet inte exakt vad som gör mig förvirrad men, jag tänker typ att.. måste inte figuren som ska gestalta skivan.. vara symmetrisk i alla dimensioner? Som i triangeln, och lite i linje som Johan skriver, blir inte funktionen för kurvan som skär triangeln i dess högsta punkt en annan funktion är kurvan som utgör dess bas?
Tycker det känns lite knepigt.
Och även kurvan som tangerar sidorna på triangeln.. hela formen blir ju rund, egentligen, och får inte ihop hur vi kan använda oss av en figur som bara består av linjer och funktionen för en enda kurva för att räkna ut volymen av denna figur :p där ligger förvirringen, så är det.
********
Eller blir det kanske mer så att det enda som är "runt"/ kurvat på dessa figurer är basen på dem, och resten blir att bestå av just räta linjer?
*********
På följande länkar hittar du GeoGebra-figurer som du kan rotera / förstora så att du bättre ser hur kroppen med kvadrater ser ut:
- https://www.geogebra.org/calculator/frarcywb (själva kroppen)
- https://www.geogebra.org/calculator/p72udtzu (kvadratiska skivor som bildar kroppen)
EDIT:
och här är motsvarande figurer med liksidiga trianglar:
Figuren som gestaltar skivan (kvadrat eller triangel, i exemplet) behöver inte vara symmetrisk alls. Dess form beskrivs av text, och dess dimensioner (en av kvadratens eller triangelns sidor, i exemplet) definieras av funktionen i x-y-planet.
Dvs, det förekommer ingen rotationssymmetri överhuvudtaget.
Okej, men man skulle ha kunnat ha en triangel som inte är liksidig som figur för exempel b) lika gärna?
Coola figurer, bra grej 👍
Dkcre skrev:Okej, men man skulle ha kunnat ha en triangel som inte är liksidig som figur för exempel b) lika gärna?
Coola figurer, bra grej 👍
Ja precis! Du skulle kunna ta en pepparkaksgris, eller vilken tvådimensionel figur som helst. Bara det är möjligt att matematiskt beskriva dess yta med hjälp av funktionen i x-y-planet.
Javisst är det coolt!
Okej, tack 🙂
LuMa07 skrev:På följande länkar hittar du GeoGebra-figurer som du kan rotera / förstora så att du bättre ser hur kroppen med kvadrater ser ut:
- https://www.geogebra.org/calculator/frarcywb (själva kroppen)
- https://www.geogebra.org/calculator/p72udtzu (kvadratiska skivor som bildar kroppen)
EDIT:
och här är motsvarande figurer med liksidiga trianglar:
Fina bilder. Hur skapar man dessa?
Trinity2 skrev:LuMa07 skrev:...
Fina bilder. Hur skapar man dessa?
Tyvärr känner jag inte till något enkelt/automatiserat sätt att skapa sådana figurer. Jag fick ta fram en parameterisering av respektive kropps yta och sedan mata in parameterytorna m.h.a. kommandot Surface(...) / Yta(...) för själva kroppen, respektive kombinera Sequence(...) / Talföljd(...) med Polygon(...) för skivorna.
Trinity2 skrev:
Fina bilder. Hur skapar man dessa?
Om du klickar du på "Algebra" i menyn till vänster kan du se vad för kommandon som använts.





