"Skriv ett uttryck för arean hos den triangel som har sina hörn..."
Hej! Jag är medveten om att denna uppgift tidigare lösts på denna sida, jag blir dock inte helt klok av att läsa igenom dessa lösningsförslag.
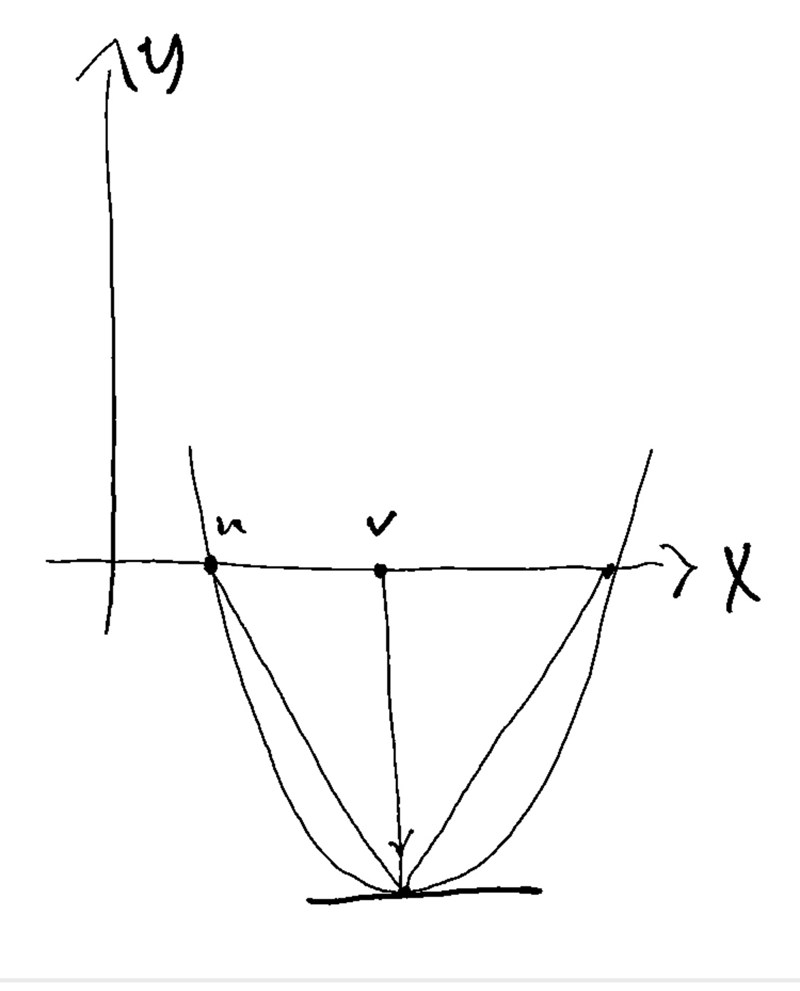
Uppgiften: En andragradsfunktion f(x) = ax^2 + bx + c (där a>0) har två nollställe, varav det ena är x=u. Derivatans nollställe är x=v. Skriv ett uttryck för arean hos den triangel som har sina hörn i de punkter där grafen skär i x-axeln samt i funktionens minipunkt. Uttrycket får innehålla a,b,c,u,v.
Obs. Jag är lite till åldern och har inte läst matte på länge. Dvs, det som man kanske antar fått med sig från matte 2, är inte direkt färskt i minnet.
Vad vet vi redan?/Min lösning hittills:
f(x) = ax^2 + bx + c
Arean för triangel: b*h/2
1. Det är en andragradare dvs. den är symmetrisk. Jag behöver ej ta reda på det andra nollstället. Använder mig av pq för att ta reda på symmetrilinjen.
2. Symmetrilinje med pq: ax^2 + bx + c = 0 (dividerar med a på bägge sidor för att få x^2 ensamt)
a^2 + bx/a + c/a = 0
x = - (b/a)/2 +-
Symmetrilinjen = det som står innan rottecknet = -(b/a)/2
3. Jag har ritat grafen, men vet ej hur jag infogar det här.
Fråga: Symmetrilinjen, är det hela linjen dvs. "höjden", eller är det bara punkten på x?
Fråga: Har sett i en annan tråd med samma fråga att man benämner basen som 2(u-v), men jag förstår inte riktigt varför man ska subtrahera v från u för att få fram basen? testade stoppa in lite siffror och så stämde det inte med den typen av uträkning.
Jag förstår givetvis att det är ett uttryck med bas i A = b*h/2. Och om symmetrilinjen är höjden, har jag ju en del av uttrycket. Men hur tar jag reda på resten?
MVH Tacksam för hjälp.
Obs, har tagit fram även:
f'(x) = 2ax + b
2ax + b = 0 ---> x = -b/2a
Om det är till någon hjälp.
Jag tycker det är tydligt att v-u är halva basen.
Hej! Har förstått det nu också. Behövde nog läsa om det bara.
Men är det övriga korrekt så jag nu endast behöver sätta in 2(v-u)?
Symmetrilinjen är en hel linje, den med x = -b/2a. Vi har fått veta att x = v är samma sak.
Höjden är funktionens värde i den punkten.
Tänk på att funktionens värde i mittpunkten kanske är negativt, men arean av en triangel är alltid positiv.
Laguna skrev:Symmetrilinjen är en hel linje, den med x = -b/2a. Vi har fått veta att x = v är samma sak.
Höjden är funktionens värde i den punkten.
Okej, så symmetrilinjen är inte det jag fick fram via pq-formeln : (b/a)/2
utan det jag fick fram när jag satte f'(x) = 0 (2ax + b = 0 ---> x = -b/2a)
om x = v
och x = -b/2a
innebär det att basen är: (-b/2a - u) * 2 är basen då?
Ja, men eftersom kan vi också uttrycka basen som
Sen vet vi ju egentligen inte om är nollstället till höger eller till vänster om mittpunkten. Det enda vi får veta är att det är ett av nollställena. Så jag skulle säga att basen är
Rubin_S skrev:Laguna skrev:Symmetrilinjen är en hel linje, den med x = -b/2a. Vi har fått veta att x = v är samma sak.
Höjden är funktionens värde i den punkten.
Okej, så symmetrilinjen är inte det jag fick fram via pq-formeln : (b/a)/2
utan det jag fick fram när jag satte f'(x) = 0 (2ax + b = 0 ---> x = -b/2a)
Du fick -(b/a)/2 och det är samma sak som -b/2a.
Är detta korrekt uttryck för triangeln?
( 2 | v-u | * -b/2a ) / 2
som sedan borde kunna förkortas till = | v-u | * -b/2a ?
(nu förutsätter jag att x:et jag fick fram för symmetrilinjen representerar hela linjen, och inte bara den punkten)
hmm, nej inser nog nu att x inte är hela symmetrilinjen utan bara den punkten, att jag måste ta fram y också, Så jag stoppar in x i funktionen...
återkommer

Ser detta rätt ut?
Är uträkningen av symmetrilinjen egentligen onödig?
och: Är det en ok förkortning när tvåorna tar ut varandra? Tänker att rent logiskt bör det funka.
Rubin_S skrev:
Ser detta rätt ut?
Är uträkningen av symmetrilinjen egentligen onödig?
Det verkar som om det fattas en bild.
vad konstigt. jag kan se bilden. Ska testa ladda om den
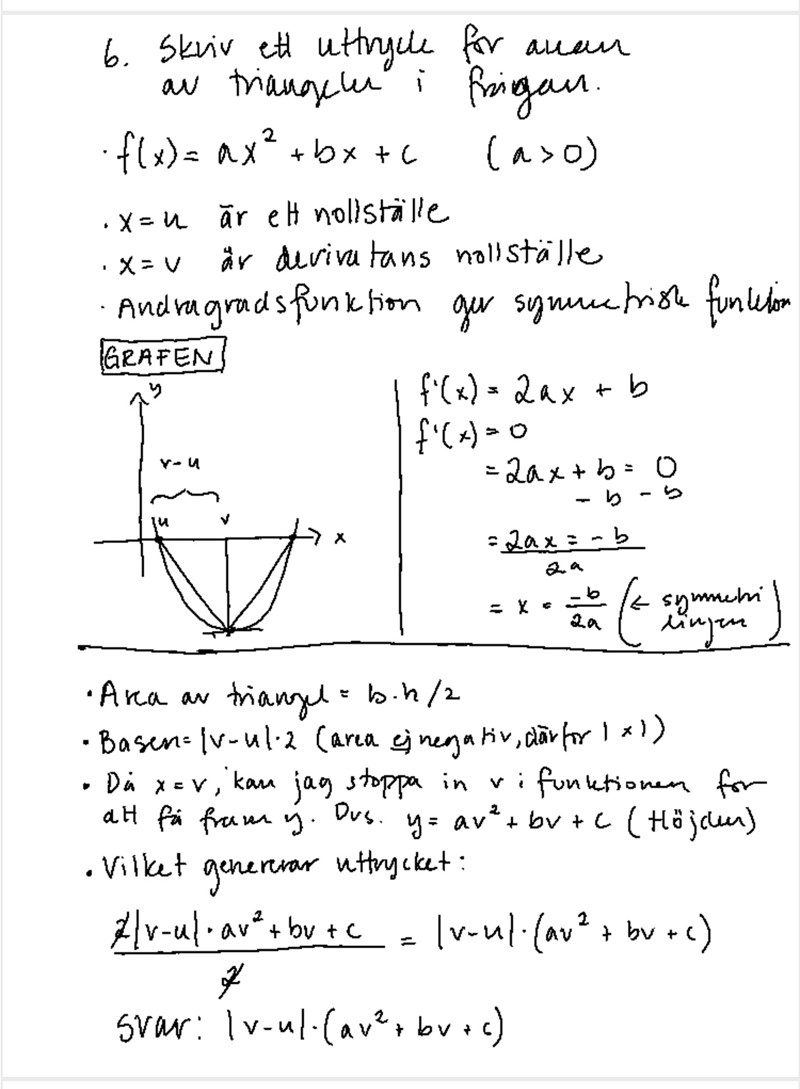
Syns den nu?
Ja, nu syns det,och det ser jättebra ut, förutom att du har missat parenteser i täljaren i ditt bråk. (Du har ju med parentesen när du har förkortat bort tvåorna.)
Tusen tack för all hjälp!
Förresten:
Hur va de nu: Är det egentligen helt onödigt att ha med uträkningen för symmetrilinjen?
För att lösa uppgiften är det inte nödvändigt att beräkna x-koordinaten för symmetrilinjen, om man bara motiverat att symmetrilinjen är dör derivatan är 0, d v s där x = v.
Eftersom är negativ (minpunkt under x-axeln) blir arean