Skriva talet på polär form
Håller på med uppgift 4310, har gjort a&b.. c&d känns lättare att fixa om det står skrivet på polär form, men hur skriver jag om z på polär form ?
Jag tog term för term först, men hur gör jag för att slå ihop termerna så det står skrivet på z=r(cosv+isinv) ?
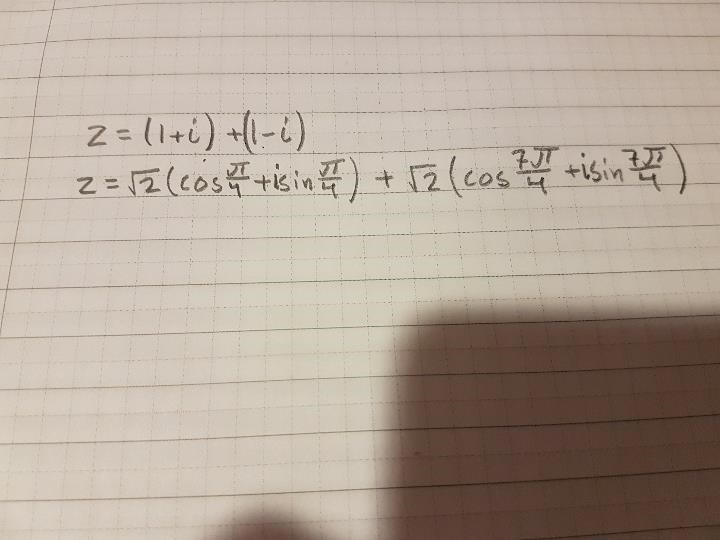
För den första kan du ju bara ta 1+i +(1-i)=2 + 0*i
z=2*( cos(0)+i*sin(0) ) , r=2 theta =0.
Rita in i komplexa tal planet är alltid bra med komplexa tal!
Egocarpo skrev:För den första kan du ju bara ta 1+i +(1-i)=2 + 0*i
z=2*( cos(0)+i*sin(0) ) , r=2 theta =0.
Får det inte till att stämma ändå, r=2 , (cos(0)+i*sin(0))=1
z=(2^3)*1 = 8
Svaret är -4
poijjan skrev:Egocarpo skrev:För den första kan du ju bara ta 1+i +(1-i)=2 + 0*i
z=2*( cos(0)+i*sin(0) ) , r=2 theta =0.
Får det inte till att stämma ändå, r=2 , (cos(0)+i*sin(0))=1
z=(2^3)*1 = 8
Svaret är -4
4310 a) då n=1 så stämmer det väl att z=2 eller 2* (cos(0)+i*sin(0)).
Jaha du ville skriva om z=(1+i)n+(1-i)n på polär form. Har ni pratat om de moivres formel eller att skriva det på e form? Det är enkelt att gå ifrån e form till de moivres formel.
Egocarpo skrev:Jaha du ville skriva om z=(1+i)n+(1-i)n på polär form. Har ni pratat om de moivres formel eller att skriva det på e form? Det är enkelt att gå ifrån e form till de moivres formel.
e-form har jag inte kommit till ännu, håller på med avsnittet om de moivres formel nu.
a) löste jag på ditt sätt, b) löste jag med kvadreringsregel
Skriv om (1+i)n och (1-i)n på polär form var för sig.
Du ska ta varje del upphöjt till n genom att ta siffran framför upphöjt till n och vinkeln innuti gånger n. Sen när du är klar med det så byter du tillbaka till a+bi och plussar ihop.
e-form som ni pratade om är bara ett kortare sätt att skriva, men det betyder precis samma sak som det du gjort här, så det kommer inte hjälpa dig med uträkningarna, bara spara lite på pennan ;P Man kan skriva rot(2)* e^i*(din vinkel) istället för sin och cos.
Laguna skrev:Skriv om (1+i)n och (1-i)n på polär form var för sig.
Det har jag gjort , men ville slå ihop dessa termer också så det står som z=r(cosv+isinv) men där tog det stop.. men inser nu att det kanske är onödigt . Men om jag ändå skulle vilja , hur göra?
Går inte, oftast iaf.
Micimacko skrev:Går inte, oftast iaf.
Missade ditt första inlägg, tack för supporten!
Micimacko skrev:Går inte, oftast iaf.
Var för snabb på "nöjd med hjälpen knappen" märkte jag nu..
Om jag sätter n=3 i sista termen jag skrev om på polär form :
får inte ut någon standardvinkel för cos & sin ?




