Skulle det gå att beräkna den med skrivmetoden, och cylindriskt skal?

Med skriv metoden skulle jag beräkna ett utryck för en ihålig skiva genom utryck för den större radien*pi minus utryck för den mindre radien*pi för dessa två omdråden ifrån y=-1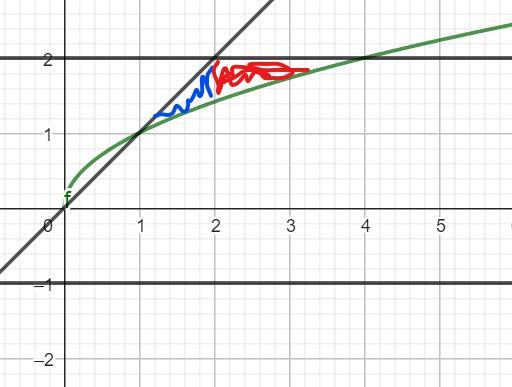

Sedan skulle jag beräkna volymen genom additionen av dessa två integraler som utgörs av dessa skivor inom dessa två områden, 2>=x>=1 och 4>=x>=2.

Sammanfattningsvis den blåa volymen+den röda volymen, färgerna med hänsyn till bilden :)

Jag får fel svar denna väg skulle någon kunna förklara om mitt tänk är rätt eller fel, i så fall också visa en korrekt uträkning genom denna väg då det förmodligen beror på nå slarv fel som jag inte hittar.
___________________________________________________________________

Sedan finns det en metod kallad för cylindriskt skal som jag har svårt att förstå?
Är ett cylindriskt skal arean som utgörs av omdrådet alltså hela arean av området, sedan det hela vägen runt för volymen, jag tänker att den arean snurrar runt mittpunkten y=-1, skulle man då behöva typ ta arean multiplicerat med omkretsen eller är det mer komplicerat än så? man behöver ju klämma in ett oändligt antal areaor i hela omkretsen för att få volymen.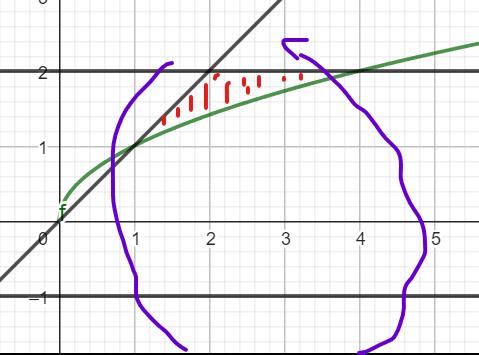

Här är en misslyckad lösning genom skrivmetoden, genom att använda den merod beskriven högst upp i mitt första medelande, vad gick snett? rätt svar ska vara 14.1 v.e

Du har ställt upp integralerna korrekt, men något har gått fel när du slagit på räknaren

Till exempel är

$\displaystyle[\pi\left(\frac{x^3}{3}+\frac{x^2}{2}-\frac{4 x^{3/2}}{3}\right)]_1^2\approx 4.38$

Nästa integral (från 2 till 4) verkar dock ha blivit korrekt (dvs 9.75329).

D4NIEL skrev:
Du har ställt upp integralerna korrekt, men något har gått fel när du slagit på räknaren

Till exempel är

$\displaystyle[\pi\left(\frac{x^3}{3}+\frac{x^2}{2}-\frac{4 x^{3/2}}{3}\right)]_1^2\approx 4.38$

Nästa integral (från 2 till 4) verkar dock ha blivit korrekt (dvs 9.75329).

tack för hjälpen, räknat om ett flertal gångr, det hela blir som en röra i skallen.

Kanske missade du att det ska vara $\frac{4}{3}x^{\frac{3}{2}}$ i sista termen i första integralen, det den primitiva funktionen du skrivit ned är lite otydlig där.

Hursomhelst blir det korrekt bara man håller tungan rätt i munnen när man sätter in gränserna :)

D4NIEL skrev:
Kanske missade du att det ska vara $\frac{4}{3}x^{\frac{3}{2}}$ i sista termen i första integralen, det den primitiva funktionen du skrivit ned är lite otydlig där.

Hursomhelst blir det korrekt bara man håller tungan rätt i munnen när man sätter in gränserna :)

fenomenalt!

Hur skulle man beräkna denna med cylindrisktskal? jag tänker mig att jag beräknar arean av området sedan försöker jag multiplicera det med omkretsen eller typ nå liknande, längden det är runt.

Ett cylindriskt skal vid koordinaten $y$ har en radie $r=y+1$ och därmed en omkrets $O=2\pi r$ , dvs $O(y)=2\pi (y+1)$ .

Varje skal har en höjd $h$ som är lika med det horisontella avståndet mellan grafen $y=x$ och $y=\sqrt{x}$ , vilket ger oss $h(y)=y^2-y$ .

Med tjocklek $\operatorname dy$ får vi att varje skal ger ett bidrag till den totala volymen som är $O(y)\cdot h(y)\cdot\operatorname dy$ .

Eftersom området bestäms av $1\leq y\leq2$ så får vi att volymen $V=\int_{1}^{2}2\pi (y+1)(y^2-y)\operatorname dy$

Svara

Visa senaste svar