Slumpförsök med flera föremål eller steg, urn-problem.

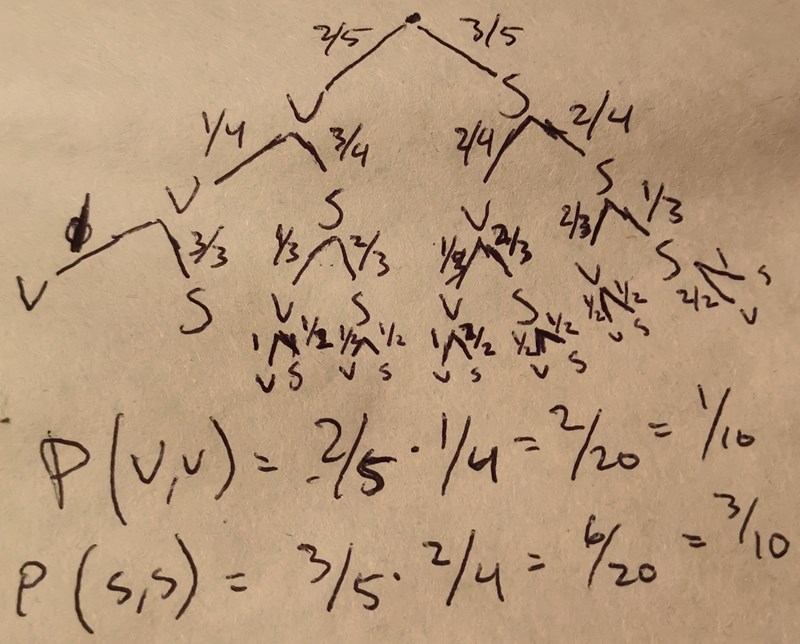
Hur ska jag tänka för att pröva om frågan stämmer?
Jämföra vinst med förlust antar jag. Men sen vet jag inte riktigt
Man vet inte hur många det finns av varje, antar jag?
Urnan finns i figuren.
3 svarta och 2 vita
Edit:
Det finns 3 olika statusar man har när man spelar detta spel:
1. man har dragit fler svarta än vita -> dra en till
2. man har dragit fler vita än svarta -> sluta
3. man har dragit lika många av varje -> sluta (det är det här som är det hemliga strategin)
Rita ett träddiagram över utfallen och räkna ut sannolikheterna.
Edit 2:
Frågan handlar bara om 1 och 2 så det som gör att det fungerar är 3.
3 kan ju vara mycket större än de andra men det spelar ingen roll bara 2 är dubbelt så stor som 1.
Det kunde ha varit ett exempel, bara. (Då får vi den roliga extrauppgiften att generalisera frågan: för vilka antal vita och svarta kulor gäller detta?)
En strategi innebär anvisningar om när man ska sluta, beroende på var i trädet man har hamnat. (En strategi i spel innefattar alla val man gör, men här finns inte så många val.) Så vad är strategin här?
Laguna skrev:En strategi innebär anvisningar om när man ska sluta, beroende på var i trädet man har hamnat. (En strategi i spel innefattar alla val man gör, men här finns inte så många val.) Så vad är strategin här?
men ... <snyft> ... min strategi uppfyller väl det .. eller?
Jaha, jag såg inte att du beskrev en strategi, det var riktat till trådskaparen.
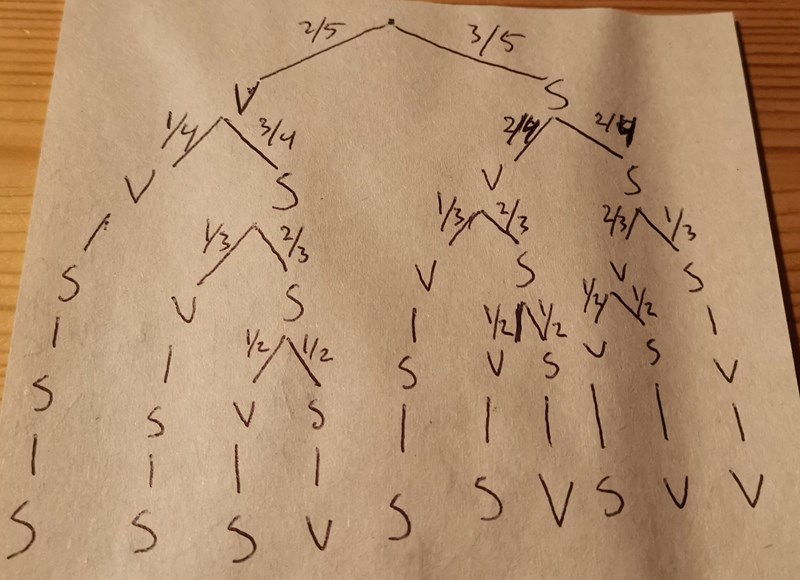
Ok. Jag har ritat ett diagram.
Men jag förstår inte riktigt hur jag ska räkna ut strategin?
Eftersom vi ska hitta en strategi som ger plus med dubbelt så stor sannolikhet som minus så kan man försöka maximera sannolikheten för plus och se var vi hamnar.
I så fall kan du beskära trädet, för det finns lägen där det är bäst att stanna och inte dra nån mer kula.
P(vinst, vinst) =2/5*1/4= 1/10
Var ska jag beskära träden.
Facit beskär trädet direkt vid först vinst.
Jag förstår inte detta
Om du ligger plus är det lika bra att sluta, för annars riskerar du att gå minus till slut, och du vill maximera sannolikheten för plus.
Men låt oss säga att vi har dragit kula och vinner. P=2/5. Då stannar vi där.
Och detta är att maximera vinsten. Annars riskerar vi att förlora.
Och nu vill vi förlora så mycket som möjligt?
P förlora) =3/5* 2/4* 1/3=1/10
Nej, vi vill fortfarande gå plus, så om vi först drog en svart kula så får vi fortsätta och hoppas att det kommer en vit senare.
Klipp bort det ur trädet som inte nås, och beräkna sannolikheterna för det som är kvar.
joculator skrev:1. man har dragit fler svarta än vita -> dra en till
2. man har dragit fler vita än svarta -> sluta
3. man har dragit lika många av varje -> slutaRita ett träddiagram över utfallen och räkna ut sannolikheterna.
Vad är det du tycker är oklart med detta?
På 1) kan man sluta om man dragit 3 svarta (det påverkar inte sannolikheten men gör det enklare att räkna.
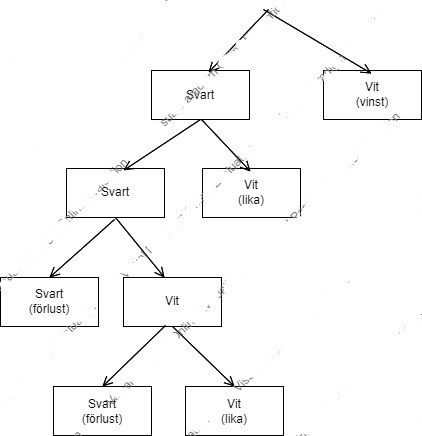
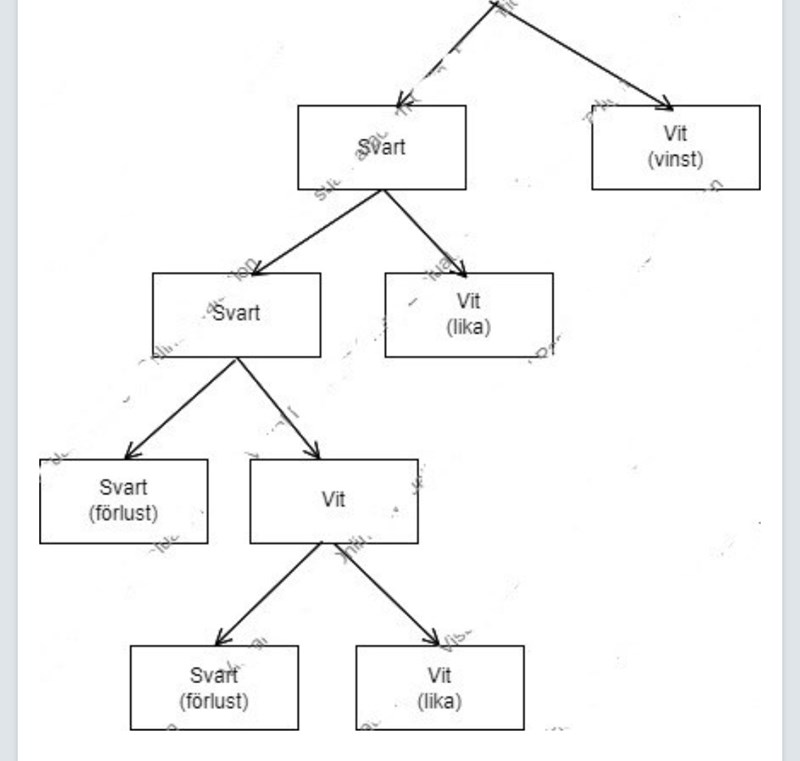
Varför skär du trädet som du gör?
Vad är poängen med det?
Du söker väl efter sannolikheten att förlora totalt, dvs 3 svarta kulor?
Och om vill vill vinna, varför stannar vi på lika vid den första förgrening på S och V?
Tillägg: 17 dec 2021 17:34
Jag fick läsa om och om igen.
Jag tror jag har förstått uppgiften nu.




