Slutsats funktion
 Behöver hjälp med denna uppgift, tror jag inte tänker rätt men har iaf tänkt såhär
Behöver hjälp med denna uppgift, tror jag inte tänker rätt men har iaf tänkt såhär
a) om p(x)=x så är g(x)=x^2. Då kan alltså g(x) vara både avtagande och växande. Växande då x>0 och avtagande då x<0.
b) p(x)=x ger g(x)=x^2. Och dom frågar alltså vad g(x) är då x>0?? Då måste g(x) vara alltså växande?
c) p(x)=x ger g(x)=x^2. Och nu frågar dom istället vad g(x) är då x<0.?? Och då måste g(x) vara avtagande?
d) tänkte samma som i a) att g(x) kan vara både avtagande och växande.
e) p(x)=-x ger g(x)=(-x)^2 => g(x)=x^2, då x>0 så är g(x) växande. Men det är fel, då i facit står att g(x) är avtagande.
f) p(x)=-x ger g(x)=x^2 då x<0 så kommer g(x) vara avtagande. Men det är också fel för att i facit står det att g(x) är växande.
Jag tror att du skulle ha stor nytta av att rita en skiss över hur p(x) kan se ut i vart och ett av fallen a) - f).
Tänk också på att rita flera förslag på p(x) i de fall där du inte vet om p(x) är positiv eller negativ. I till exempel det första fallet a) gäller det alltså att rita både p(x) positiv och p(x) negativ, för att se alla möjligheter.
Bubo skrev:Jag tror att du skulle ha stor nytta av att rita en skiss över hur p(x) kan se ut i vart och ett av fallen a) - f).
Tänk också på att rita flera förslag på p(x) i de fall där du inte vet om p(x) är positiv eller negativ. I till exempel det första fallet a) gäller det alltså att rita både p(x) positiv och p(x) negativ, för att se alla möjligheter.
Förstår inte varför jag ska rita? Varför ska jag rita p(x) som en negativ funktion när det står i uppgift a) att p(x) är växande?
Vad är det jag ska kolla på när jag har ritat?
Förstår inte varför jag ska rita? Varför ska jag rita p(x) som en negativ funktion när det står i uppgift a) att p(x) är växande?
Vad är det jag ska kolla på när jag har ritat?
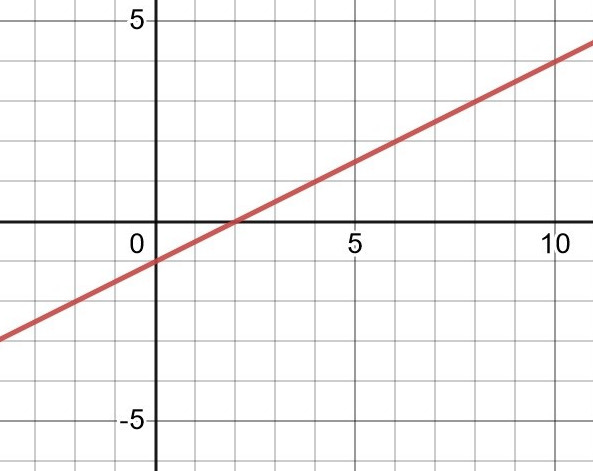
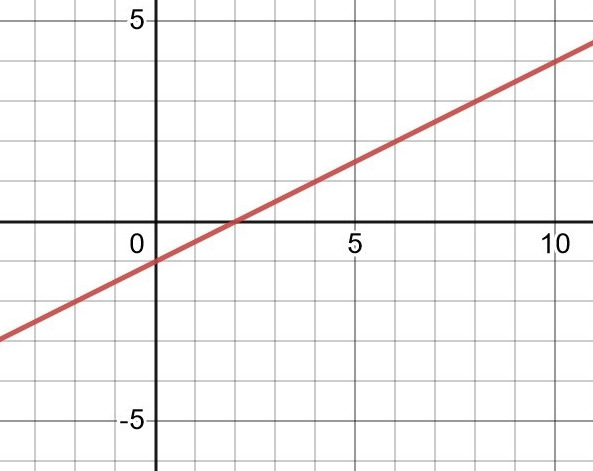
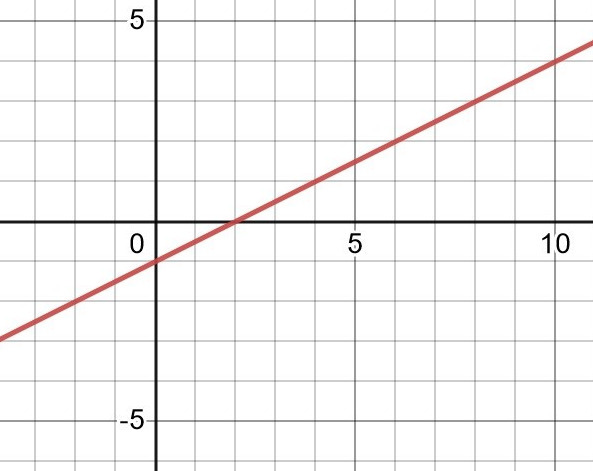
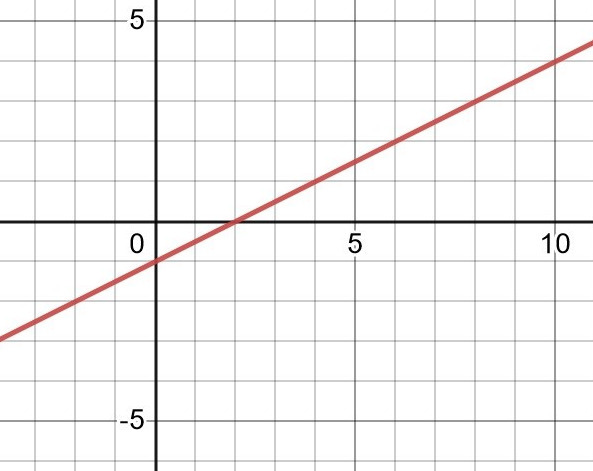
Om du ritar, måste du sätta dig in i vad det verkligen står skrivet, och då skulle du inse att a-uppgiften exempelvis kan illustreras av den här bilden:
Smaragdalena skrev:Förstår inte varför jag ska rita? Varför ska jag rita p(x) som en negativ funktion när det står i uppgift a) att p(x) är växande?
Vad är det jag ska kolla på när jag har ritat?
Om du ritar, måste du sätta dig in i vad det verkligen står skrivet, och då skulle du inse att a-uppgiften exempelvis kan illustreras av den här bilden:
Hm, försöker förstå men har inte lyckats än.
Antar att funktionen du ritade är p(x).
Och att den är ritad som p(x)=0,5x-1. Det är en växande funktion för alla x-värden i definitonsmängden, vilket uppgift a) ville att p(x) skulle vara.
Då är g(x)=(0,5x-1)^2. Funktionens nollställe är x=2 alltså, blir kurvan g(x) växande när x>2 och avtagande när x<2
På b-uppgiften kan funktionen exempelvis se ut så här:
.jpg?width=800&upscale=false)
Smaragdalena skrev:På b-uppgiften kan funktionen exempelvis se ut så här:
Förstår inte, tänker jag fel på uppgift a) ?
Nu i uppgift b) har du ritat en exponentialfunktion, är det den som är p(x)? ska jag ta reda på vad g(x) är med hjälp av den?
jordgubbe skrev:Smaragdalena skrev:Förstår inte varför jag ska rita? Varför ska jag rita p(x) som en negativ funktion när det står i uppgift a) att p(x) är växande?
Vad är det jag ska kolla på när jag har ritat?
Om du ritar, måste du sätta dig in i vad det verkligen står skrivet, och då skulle du inse att a-uppgiften exempelvis kan illustreras av den här bilden:
Hm, försöker förstå men har inte lyckats än.
Antar att funktionen du ritade är p(x).
Och att den är ritad som p(x)=0,5x-1. Det är en växande funktion för alla x-värden i definitonsmängden, vilket uppgift a) ville att p(x) skulle vara.
Då är g(x)=(0,5x-1)^2. Funktionens nollställe är x=2 alltså, blir kurvan g(x) växande när x>2 och avtagande när x<2
Har g(x) något nollställe?
jordgubbe skrev:Smaragdalena skrev:På b-uppgiften kan funktionen exempelvis se ut så här:
Förstår inte, tänker jag fel på uppgift a) ?
Nu i uppgift b) har du ritat en exponentialfunktion, är det den som är p(x)? ska jag ta reda på vad g(x) är med hjälp av den?
När jag svarade tänkte jag att du var klar och att du skulle gå vidare. Nu när jag har tänkt lite till kom jag på att det var något som saknades på a-uppgiften, så nu har jag svarat en gång till på det.
Funktionen i b-uppgiften kan exempelvis vara en exponentialkurva, men det finns andra varianger också som uppfyller kraven (men det enklaste för mig var att rita en exponentialkurva, så det gjorde jag - varför krångla till det när det inte behövs?). Vad kan man säga om g(x) i det här fallet? Positiv? Negativ? Nollställen?
Smaragdalena skrev:jordgubbe skrev:Smaragdalena skrev:Förstår inte varför jag ska rita? Varför ska jag rita p(x) som en negativ funktion när det står i uppgift a) att p(x) är växande?
Vad är det jag ska kolla på när jag har ritat?
Om du ritar, måste du sätta dig in i vad det verkligen står skrivet, och då skulle du inse att a-uppgiften exempelvis kan illustreras av den här bilden:
Hm, försöker förstå men har inte lyckats än.
Antar att funktionen du ritade är p(x).
Och att den är ritad som p(x)=0,5x-1. Det är en växande funktion för alla x-värden i definitonsmängden, vilket uppgift a) ville att p(x) skulle vara.
Då är g(x)=(0,5x-1)^2. Funktionens nollställe är x=2 alltså, blir kurvan g(x) växande när x>2 och avtagande när x<2
Har g(x) något nollställe?
om g(x)=(0,5x-1)^2, så kommer nollstället att vara x=2
Smaragdalena skrev:jordgubbe skrev:Smaragdalena skrev:På b-uppgiften kan funktionen exempelvis se ut så här:
Förstår inte, tänker jag fel på uppgift a) ?
Nu i uppgift b) har du ritat en exponentialfunktion, är det den som är p(x)? ska jag ta reda på vad g(x) är med hjälp av den?
När jag svarade tänkte jag att du var klar och att du skulle gå vidare. Nu när jag har tänkt lite till kom jag på att det var något som saknades på a-uppgiften, så nu har jag svarat en gång till på det.
Funktionen i b-uppgiften kan exempelvis vara en exponentialkurva, men det finns andra varianger också som uppfyller kraven (men det enklaste för mig var att rita en exponentialkurva, så det gjorde jag - varför krångla till det när det inte behövs?). Vad kan man säga om g(x) i det här fallet? Positiv? Negativ? Nollställen?
jag tror att funktion som du har ritat är p(x)=2^x , och då kommer g(x)=(2^x)^2. Och, om jag kollar med grafräknare hur g(x) ser ut så ser jag att det är en växande funktion.
Men jag har en fråga till, på b) skulle p(x) också exempelvis kunna vara p(x)=-(x^3) ?
nej, tänkte fel kan inte alls vara p(x)=-(x)^3
Du har rätt i att p(x) inte kan vara -x3. Vad är det som gör att det inte fungerar?
Smaragdalena skrev:Du har rätt i att p(x) inte kan vara -x3. Vad är det som gör att det inte fungerar?
Eftersom det kommer att vara en avtagande funktion, vilket p(x) inte skulle vara.
Tror jag förstår nu hur man ska tänka, har lyckats lösa dom andra också, men använde exponentialfunktion på vissa andra uppgifter också.
Har tänkt jättelänge på någon annan slags funktion som man skulle kunna ha istället för en exponentialfunktion, kommer inte på någon. Vad för annan funktion skulle det kunna vara på exempelvis b) uppgiften istället för exponentialfunktion?
En konstant funktion är både växande och avtagande samtidigt (men varken strängt växande eller strängt avtagande) så y = 5 är en funktion som är både växande och positiv, samt avtagande och positiv. man kan också tänka sig funktioner som är definierade på olika sätt i olika intervall, eller exempelvis y = 1,2x+5. Men som jag skrev tidigare - en exponentialfunktion är det enklaste exemplet jag kan komma på.