Smartare lösning?
Hej!
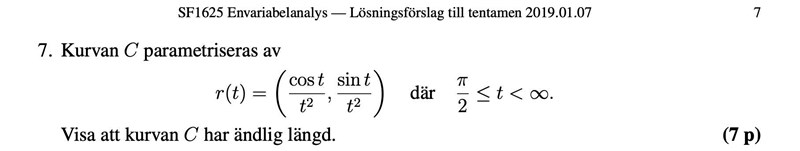
Jag undrar att det finns en smart lösning till det, till exempel att man ser direkt att
Dvs en ellips-cirkel med små och stor axel , eller nåt sånt. För att undvika lösa på detta sätt:

Vad händer om du skriver på polär form?
Hur menar du?
Alltså uttrycker kruvan med polära variabler?
Ja, jag förstår vad ni säger :) men jag vet inte hur ni menar med det. Det är redan i trigonometrisk form. Kan ni skriva vad ni menar?
Ja, bara för att det finns trigonometriska funktioner i parametrarna betyder det ju inte att det är skrivet i polär form än!
Det är nog bäst att vi väntar på någon annan, det här ligger inte på min nivå av matte så att säga.
Kurvan C är en cirkulär spiral med centrum i origo som snabbt spiraliserar in mot origo.
Laguna menar bara (förmodligen) att man kan slippa behovet av alla de där trigonometriska utskrivningarna om man använder kompaktare beteckningar som
där
Där kruxet alltså är att utnyttja att och .
Är samma princip. Bara en fråga om att använda vektoralgebra och några memorerade formler för att slippa göra hela trigonometriska utskrivningen.
Även någon underlighet i din lösning på sista raden när du tar bort rotenurtecknet dajamanté.
Det kan förstås även vara intressant att fundera på om det finns något allmänt kriterium för när en monotont minskande spiral, dvs en funktion på formen där är en minskande funktion konvergerande mot 0, ska ha divergent area.
Notera att det inte är nödvändigt att beräkna kurvans längd för att lösa uppgiften; det räcker att finna en ändlig övre begränsning till kurvans längd.
Till exempel är
och integralen av denna funktion är ändlig.
dajamanté skrev:Ja, jag förstår vad ni säger :) men jag vet inte hur ni menar med det. Det är redan i trigonometrisk form. Kan ni skriva vad ni menar?
Jag menade att parametrisera den som . Just när det är sin och cos i x/y-koordinaterna kan det vara bra. Men sen kommer väl trigonometrin tillbaka när man ska beräkna kurvlängden så jag vet inte om det var nån användbar idé.

Dags för mig att stänga butiken för dagen... tack för alla svar, jag återkommer imorgon med mer förvirring!
Edit: jag måste säga att jag förstår ingenting om spiralerna...
@SkarpBläckfisk : ja, min lösning är säkert full med slarv till o med...
Albiki skrev:Kurvan C är en cirkulär spiral med centrum i origo som snabbt spiraliserar in mot origo.
God morgon! Butiken har öppets.
Jag har aldrig sett spiralensekvation tidigare.
Hur kom du fram till att var lika med ?
SeriousCephalopod skrev:Laguna menar bara (förmodligen) att man kan slippa behovet av alla de där trigonometriska utskrivningarna om man använder kompaktare beteckningar som
där
Parametrisering med vilda hattar har jag inte sett förut heller.
Jag förstår inte heller vad har hänt med derivata, och varför du har vilda hat, och vilda hat prime när du deriverar f.
Laguna skrev:Jag menade att parametrisera den som . Just när det är sin och cos i x/y-koordinaterna kan det vara bra. Men sen kommer väl trigonometrin tillbaka när man ska beräkna kurvlängden så jag vet inte om det var nån användbar idé.
Jag är ledsen, jag ser inte alls hur det här har gått till:
Om , bör inte eller något i detta ända?
dajamanté skrev:Laguna skrev:Jag menade att parametrisera den som . Just när det är sin och cos i x/y-koordinaterna kan det vara bra. Men sen kommer väl trigonometrin tillbaka när man ska beräkna kurvlängden så jag vet inte om det var nån användbar idé.
Jag är ledsen, jag ser inte alls hur det här har gått till:
Om , bör inte eller något i detta ända?
Om du inte har lärt dig polära koordinater så var nog allt jag skrev ganska kryptiskt.
Om du ritar en bild så kan jag peka. Eller läs https://sv.wikipedia.org/wiki/Pol%C3%A4ra_koordinater.
dajamanté skrev:Albiki skrev:Kurvan C är en cirkulär spiral med centrum i origo som snabbt spiraliserar in mot origo.
God morgon! Butiken har öppets.
Jag har aldrig sett spiralensekvation tidigare.
Hur kom du fram till att var lika med ?
Kvadrera och addera så får du trigonometriska ettan i täljaren.
Men varför skulle får jag addera båda parameter överhuvudtaget?
dajamanté skrev:SeriousCephalopod skrev:...
Parametrisering med vilda hattar har jag inte sett förut heller.
Jag förstår inte heller vad har hänt med derivata, och varför du har vilda hat, och vilda hat prime när du deriverar f.
Hatt är en symbol som används för att beteckna att en vektorstorhet har längd 1. Hattar är sedan en av flera alternativa system för att beteckna enhetsvektorer alternativt betecknar enhetsvektorerna när man håller på med sfäriska koordinater.
Det är inte ovanligt att man använder för enhetsvektorerna i det kartesiska systemet.
Poängen här var dock att packa ihop till en enda symbol betecknades en vektor för att slippa skriva lika mycket men den symbolen kunde lika gärna varit eller något annat. Metoden är dock inte till karaktären annorlunda från din metod och ska bara ses som ett kompaktare och därmed snabbare sätt att skriva saker men är inte i övrigt en ny metod.
På temat av att skriva saker på olika sätt så kan man också, eftersom kurvan är ligger i planet, undvika vektoralgebra helt och arbeta direkt med komplexa tal istället. Då skulle man kunna skriva funktionen som en komplexvärd funktion
Stegen är likadana som med vektorrepresentationen men utifall man är mer rutinerad med komplexa tal så blir detta lite lättare att följa.
Laguna skrev:
Om du inte har lärt dig polära koordinater så var nog allt jag skrev ganska kryptiskt.Om du ritar en bild så kan jag peka. Eller läs https://sv.wikipedia.org/wiki/Pol%C3%A4ra_koordinater.
Nej nej det har jag gjort i matte 4, men just nu visste jag inte hur jag kan applicera det till en kurva som är redan parametriserad med sin och cos.
SeriousCephalopod skrev:dajamanté skrev:SeriousCephalopod skrev:...
Parametrisering med vilda hattar har jag inte sett förut heller.
Jag förstår inte heller vad har hänt med derivata, och varför du har vilda hat, och vilda hat prime när du deriverar f.
Hatt är en symbol som används för att beteckna att en vektorstorhet har längd 1. Hattar är sedan en av flera alternativa system för att beteckna enhetsvektorer alternativt betecknar enhetsvektorerna när man håller på med sfäriska koordinater.
Det är inte ovanligt att man använder för enhetsvektorerna i det kartesiska systemet.
Poängen här var dock att packa ihop till en enda symbol betecknades en vektor för att slippa skriva lika mycket men den symbolen kunde lika gärna varit eller något annat. Metoden är dock inte till karaktären annorlunda från din metod och ska bara ses som ett kompaktare och därmed snabbare sätt att skriva saker men är inte i övrigt en ny metod.
Ja, det har jag sett hos 3 brown one blue. Så när du deriverar en hat, måste du plussa på alla inre derivator?





