rotationskropp

Har du ritat? Lägg upp bilden här!

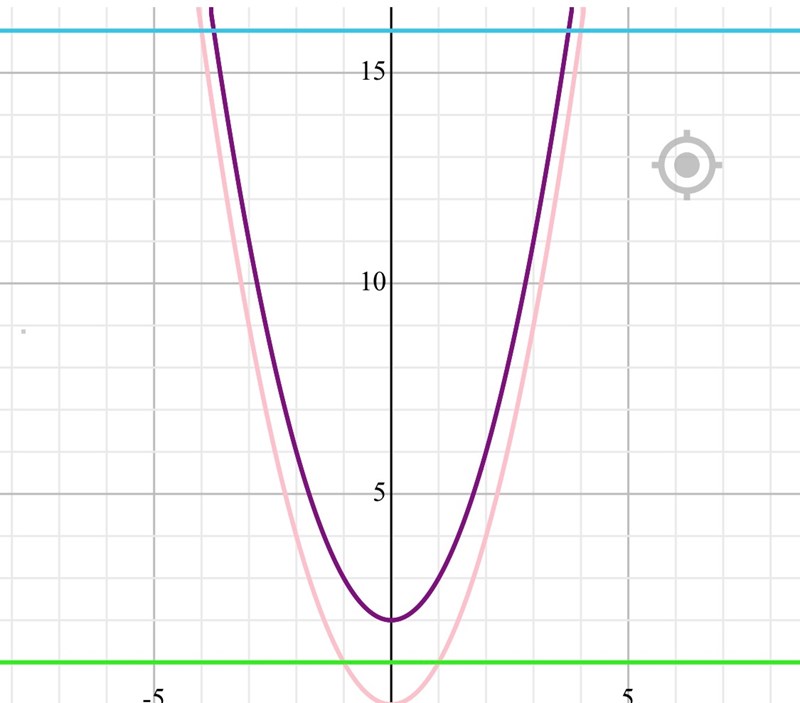såhär ser det ut, menas det att det är området till höger om x axeln?

Ja. I det här fallet hade det blivit samma resultat om man roterar högra delen, vänstra delen eller hela kurvan, men det ärinte alltid så.

Okej, behöver man då utgå ifrån det när man räknar och dela skivorna på 2? eller kan man göra som vanligt?

Jag skulle gå på uppgiftstexten och göra som vanligt.

när jag beräknar den inre kroppen (hålet). Och ställer upp integrationsgränserna. Ska jag då ställa från 16–> 2 på den. Istället för 16–> som på den andra. Eftersom att denna yta startar vid y=2

Om du räknar ut yttervolymen och innervolymen (hålet) separat - ja.

När man räknar på volymen o ställer upp, integralen mellan 16 till 2 för (πy-2) dy.

så kan man ju sätta π utanför integralen o därefter bara integrera y, kan jag göra detsamma med -2? Och alltså sätta π-2 utanför integralen?

Jag förstår inte vad du menar. Jag skulle beräkna rotationsintegralen från 0 till 16 med den yttre kurvan som integrand, minus rotationsintegralen från 2 till 16 med den inre kurvan sm integrand. Eller så skulle jag göra en integral från 0 till 2 där varje skiva är en cirkelskiva plus en integral från 2 till 16 där varje skiva är en cirkelring (d v s med hål i mitten).

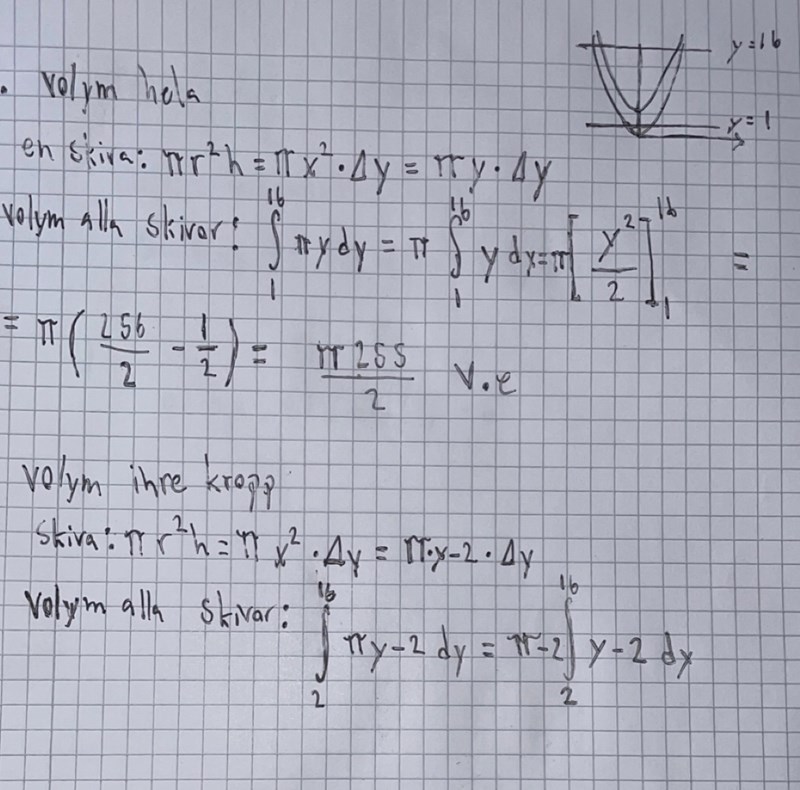såhär har jag gjort hittils, jag har beräknat rotationsintegralen för den yttre kurvan från 1till 16 eftersom att ytan skärs då y=1

där nere har jag börjat på den inre volymen, som jag sedan ska subtrahera från den totala

Ah, då vill jag ändra siffran 0 till 1 i mitt förra inlägg. Jag hade glömt att de hade den gränsen.

Skall det vara $\pi y-2$ eller $\pi(y-2)$ som integrand?

Kurvan är y=x²+2

så det blir väll egenligen så att Volymen inre: πx²dy

så integranden blri väll π(y-2), glömde parantesen. Antar att det inte går att lägga tvåan utanför i det fallet.

Har glömt bort helt hur jag gör för att få fram rätt primitiva funktion här y blir ju $\frac{y^2}{2}$, pi läggs utanför intergralen. Men har gör jag med tvåan, blir det 2y? Alltså $\frac{y^2-2y}{2}$

Du kan och bör alltid kontrollera ditt förslag på primitiv funktion genom att derivera det.

Om du då får tillbaka ursprungsfunktionen så var ditt förslag rätt, annars inte. 

(Detta pga att om F(x) är en primitiv funktion till f(x) så gäller det att F'(x) = f(x).)

Derivera därför ditt förslag på pimitiv funktion. Vad får du för resultat?

Rent spontant känns det som det är rätt, nämnaren försvinner när jag multiplicerar med 2.-2y blir 2 och y² blir ju y sedan. 

Nej det stämmer inte.

Visa i detalj hur du gör när du deriverar $\frac{y^2-2y}{2}$ så kan vi hjälpa dig att hitta felet.

blått är de steg jag genomfört vid derivering

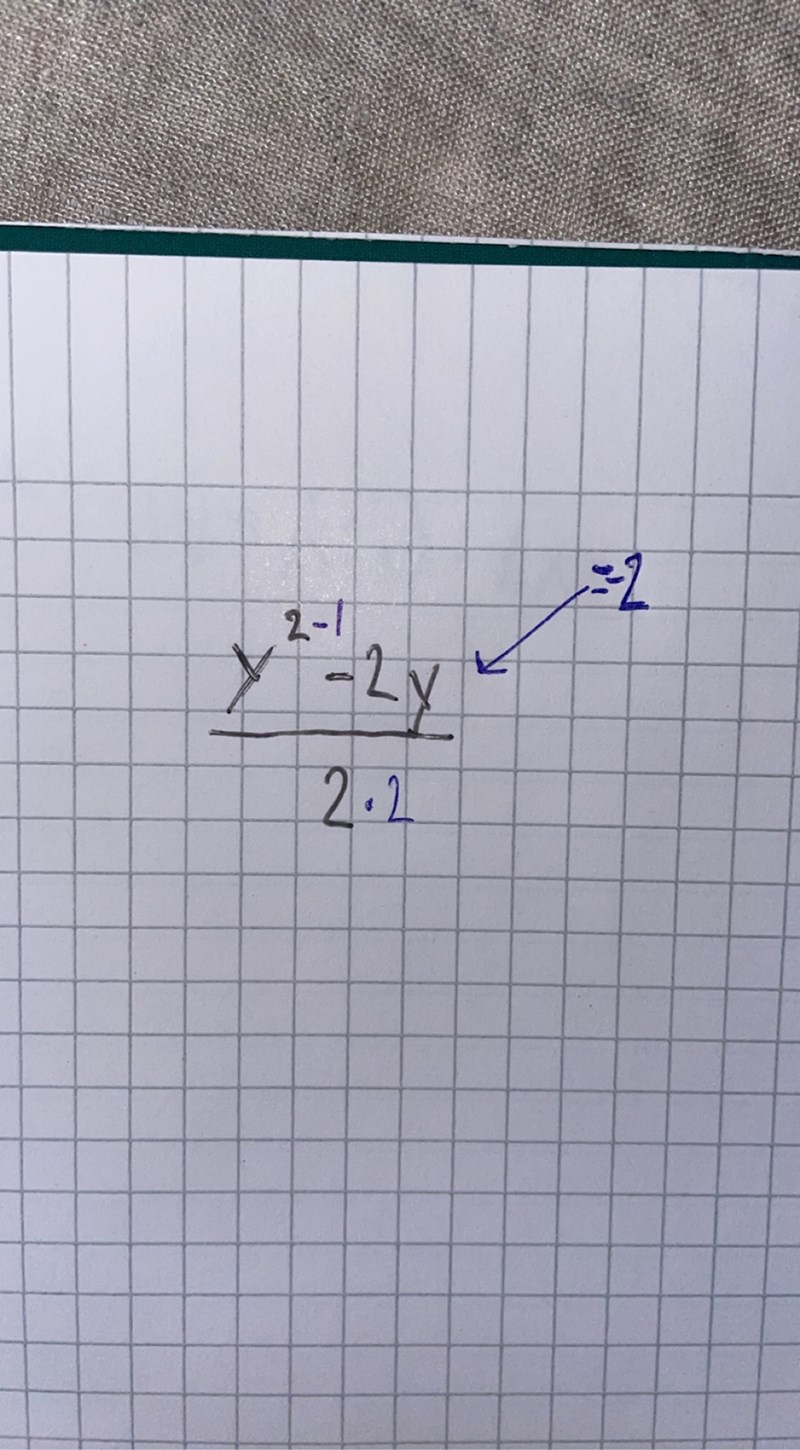
Jag förstår inte. Är det så här du tänker?

• Jag deriverar täljarens första term och får då 2y.
• Jag deriverar täljarens andra term och får då-2.
• Jag dividerar täljarens första term med 2.
• Jag multiplicerar nämnaren med 2.

I så fall har du

1. multiplicerat nämnaren med 2 utan att multiplicera täljaren med 2, vilket förändrar bråkets värde.
2. dividerat en av täljarens termer med 2 utan att göra något med vare sig nämnaren eller den andra termen i täljaren, vilket även det förändrar bråkets värde.

==================

Jag rekommenderar att du inte försöker derivera och förenkla samtidigt utan att du istället gör det steg för steg.

Antingen först derivera och sedan förenkla, som här:  Derivatan av $\frac{y^2-2y}{2}$ är lika med derivatan av $\frac{1}{2}\cdot (y^2-2y)$, som är lika med $\frac{1}{2}\cdot (2y-2)$, vilket efter förenkling blir $y-1$.

Eller först förenkla och sedan derivera, som här: Derivatan av $\frac{y^2-2y}{2}$ är lika med derivatan av $\frac{y^2}{2}-y$, som är lika med $\frac{2y}{2}-1$, vilket efter förenkling blir $y-1$.