Spänning
Hej!
Jag har inte riktigt förstått det här med spänning i kretsar.
När vi tänker oss spänningen i en krets, försummar vi kabelns inre resistens? Om ja, varför? För det är väl ändå ganska viktigt att ta hänsyn till. Kabelns resistens borde väl sänka strömmens energi hela vägen på grund av friktion, så att potentialen ständigt sjunker?
Dessutom, i ett batteri kommer strömmen gå från den positiva polen till den negativa. Strömmen har således en potential, och denna borde sjunka närmare de kommer batteriets negativa pol? För då förlorar den ju potentiell energi.
Säg då att batteriet har spänningen 3 V. Om en resistor är i vägen kommer strömmen få en "voltage drop" på 3 V också. Men varför? Strömmen kan ju inte minska sin potential så mycket om den ständigt genom kablarna har förlorat sin potential, ju närmare den kommer minuspolen. När den är framme vid resistorn har den redan förlorat en del av sin potential. Så den kan inte förlora 3 V helt plötsligt, den har inte kvar så mycket?
Tack.
Resistansen i en kabel är i en normal krets väsentligt lägre än den belastning som kretsen har totalt och kan därför sättas till 0.
Om det är en enkel krets med ett batteri och ett motstånd så är hela spänningsfallet, (elektronerna har tröttat ut sig kanske man kan säga först då de har passerat motståndet. )
Tänk på att elektricitet närmar sig kvantmekanik och kan inte helt appliceras på vår verklighetsuppfattning.
Men jag är väldigt förvirrad. I ett homogent fält kommer ju potentialen minska när laddningen närmar sig minuspolen. Borde inte motsvarande gälla i kretsar? Att när strömmen går från positiv till negativ kommer potentialen minska successivt längs kabeln? Därför förstår jag inte hur potentialskillnaden genom en resistor kan vara lika stor som spänningen i batteriet. När strömmen kommer fram till resistorn kommer ju en del potential redan ha förlorats, för då har strömmen närmat sig negativa polen. Hur kan strömmen då förlora ännu mer potential, genom resistorn, än den hade kvar när den var framme vid resistorn?
Om man förenklar lite och säger att resistansen i själva ledningen är 0, så blir spänningsfallet över ledaren 0. Om man vill modellera en lite mer realistisk situation kan man tänka sig ledaren som en ideal ledare (d v s med resistansen 0) i serie med en (liten) resistor.
Smaragdalena skrev:Om man förenklar lite och säger att resistansen i själva ledningen är 0, så blir spänningsfallet över ledaren 0. Om man vill modellera en lite mer realistisk situation kan man tänka sig ledaren som en ideal ledare (d v s med resistansen 0) i serie med en (liten) resistor.
Jag förstår nu att resistansen hos själva ledaren försummas. Men jag förstår fortfarande inte varför totala spänningsfallet längs en ledare blir noll. Längs ledaren kommer ju strömmen komma allt närmare minuspolen, så potentialen bör sjunka?
Har lidit så länge och filofiserat runt detta så länge nu. Tre dagar har det gått. Blir oerhört glad om någon hjälper mig.
Att potentialen faller beror på att det finns en resistans. Hur mycket faller potentialen, om det är en ideal ledare, d v s om resistansen är 0?
Smaragdalena skrev:Att potentialen faller beror på att det finns en resistans. Hur mycket faller potentialen, om det är en ideal ledare, d v s om resistansen är 0?
Jag vet att det rätta svaret är 0, men rent intuitivt skulle jag säga att potentialskillnaden bör vara över 0.
Även utan resistans anser jag att strömmen borde förlora potential eftersom den kommer närmare minuspolen i t.ex. batteriet. Jag har fått veta att detta är fel men kan inte förstå varför. Jämför bara med homogena elektriska fält. Där sjunker potentialen, ju närmare plusladdningen kommer minuspolen. Varför kan inte samma sak sägas om kretsar?
Om man mäter riktigt, riktigt noga så har du nog rätt, eftersom resistansen hos ledaren inte är exakt 0.
Smaragdalena skrev:Om man mäter riktigt, riktigt noga så har du nog rätt, eftersom resistansen hos ledaren inte är exakt 0.
Det var inte så jag tänkte... jag tycker jag har varit måttligt tydlig men ska göra ett till försök.
- Anta att resistansen i en kabel är exakt 0. Strunta i om det praktiskt sett vore omöjligt, bara låt det vara så.
- Anta nu att vi har en väldigt enkel krets där kabeln går från pluspolen i ett 3V-batteri till minuspolen i samma batteri.
- På vägen finns ingen resistor och ingen annan pryl heller. Det finns bara en kabel som är ansluten till ett 3V-batteri.
- Vi sätter på strömmen och då flödar strömmen från den positiva änden i 3V-batteriet till den negativa änden.
- Min fråga är följande. Bör det totala potentialfallet inte vara 3V? Från början har ju strömmen potentialen 3V. Potential är energi per laddning. När batteriets minuspol har utfört en kraft på laddningarna och dragit de en viss sträcka längs ledaren, då har ju en viss potentiell energi övergått till rörelseenergi. Alltså sjunker potentialen längs ledaren. Till slut i kretsen bör potentialen vara helt förlorad = 0 V. Tydligen är detta fel. Jag ber nu att du pekar ut varför jag har fel.
- Jämförelsevis kan vi ta homogena elektriska fält som exempel. Om en plusladdning sitter och nuddar vid den plusladdade plattan kommer laddningen ha en viss potential. Detta då plusladdningen känner en kraft i riktningen till den minusladdade plattan. Alltså, när plusladdningen närmar sig minusplattan, kommer denna laddningen få sänkt potential.
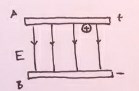
- Likadan princip borde kunna tillämpas på kretsar: att när strömmen närmar sig batteriets minussida kommer potentialen sjunka.
Låt mig snälla ha annat att tänka på under lovet än detta. Snälla hjälp mig bli klar i huvudet redan nu. :)
Hej
Jag ska göra ett försök.
När man handskas med elektriska kretsar använder man en modell där det ingår spänningskällor, resistanser och ledare att "koppla ihop" dem med. (Finns fler komponenter men vi håller oss till dessa så länge) I denna modell kan man använda ett antal matematiska samband som t.ex Ohms lag U=R x I
Kom ihåg att detta är en modell för dessa förutsättningar. För att räkna på laddningar i elektriska fält behövs en annan modell, som du beskriver.
Till din fråga: Bör det totala potentialfallet inte vara 3V?
Jo, det tycker jag. Det elektriska fältet följer helt och hållet ledaren. Det blir dock lite konstigt med resistansen 0. Det innebär att en oändlig mängd laddningar rör sig i ledaren. Kanske lättare att tänka sig en massa små resistanser i serie mellan polerna på spänningskällan. Över varje resistans får man då ett spänningsfall som motsvaras av den potentialförlust som varje laddning gör.
Hoppas jag var till någon hjälp.
Jag har fortfarande inte lyckats komma fram till ett svar.
Jag tror det kan ha att göra med min uppfattning av resistans. Som några av er har pekat ut gäller detta:
Att potentialen faller beror på att det finns en resistans.
Detta begriper jag inte. Jag ser inte sambandet mellan resistans och potential. Potentialen kommer ju sjunka automatiskt eftersom den omvandlas till rörelseenergi hos elektronerna. Rörelseenergin minskar i sin tur på p.g.a. resistans (friktion). Alltså, resistansen påverkar elektroners hastighet d.v.s. ström, men påverkar inte potential.
Än så länge har jag fått veta att resistans bara beror av friktion. Men det verkar inte alls så utifrån era svar. Vad är då resistans? Och hur kan resistans leda till potentialskillnad?
Hej
Resistans har att göra med vilket material det handlar om. Om vi tittar på metaller så har de sina atomer ordande i en så kallad kristallstruktur, eller ett tredimensionellt rutnät kanske man kan säga. Varje atom har ett antal grannar som den delar elektroner med och en del av dem är så fria att de kan flytta sig i rutnätet med hjälp av en elektrisk spänning som ansluts.
Olika metaller har olika mycket fria elektroner och därmed olika ledningsförmåga. Jag känner att jag är ute på lite hal is här, kanske nedanstående länk kan vara till hjälp:
https://www.electrical4u.com/what-is-electrical-resistance/
När man handlar om kretsar så ritar man ledare mellan komponenter som streck. Dessa symboliserar ideala ledare som inte har någon längd. Ett långt streck betyder inte att det är fysiskt långt mellan två komponenter.
Du säger att elektroners hastighet är ström men det nog inte rätt. Elektrisk ström är antalet laddningar som passerar ett tvärsnitt i en ledare, per tidsenhet.
ThomasN skrev:Hej
Resistans har att göra med vilket material det handlar om. Om vi tittar på metaller så har de sina atomer ordande i en så kallad kristallstruktur, eller ett tredimensionellt rutnät kanske man kan säga. Varje atom har ett antal grannar som den delar elektroner med och en del av dem är så fria att de kan flytta sig i rutnätet med hjälp av en elektrisk spänning som ansluts.
Olika metaller har olika mycket fria elektroner och därmed olika ledningsförmåga. Jag känner att jag är ute på lite hal is här, kanske nedanstående länk kan vara till hjälp:https://www.electrical4u.com/what-is-electrical-resistance/
När man handlar om kretsar så ritar man ledare mellan komponenter som streck. Dessa symboliserar ideala ledare som inte har någon längd. Ett långt streck betyder inte att det är fysiskt långt mellan två komponenter.
Du säger att elektroners hastighet är ström men det nog inte rätt. Elektrisk ström är antalet laddningar som passerar ett tvärsnitt i en ledare, per tidsenhet.
Hej!
Jag vet att elektroners hastighet inte är ström, men självklart finns en koppling däremellan.
Jag förstår även att olika metaller har olika resistivitet.
Men kan du snälla förklara vad som var fel specifikt, i mitt förra inlägg? Jag resonerade att potential och resistans inte har något samband. Men enligt Smaragdalena bland andra är detta falskt. Smaragdalena skrev:
Att potentialen faller beror på att det finns en resistans.
Kan du förklara varför potentialen faller när det finns en resistans? Det var det jag behövde veta. Tack.
Du kan skriva Ohms lag på formen
rI = E, där r är resistans per längdenhet hos ledaren.
Om r är mycket låg så blir den elektriska fältstyrkan E låg och därför blir potentialskillnaden mellan ledarens båda ändar också liten, om vi antar att ledaren inte är extremt lång. Strömmen i kretsen bestäms ju till största delen av resistansen hos resistorn, om vi antar att ledarens totala resistans är försumbar i sammanhanget.
Eller uttryckt annorlunda, om vi har en låg resistivitet så krävs det bara ett förhållandevis svagt elektriskt fält E för att driva strömmen genom ledaren, det blir därför ett försumbart spänningsfall över ledaren.
Stenenbert skrev:Smaragdalena skrev:Om man mäter riktigt, riktigt noga så har du nog rätt, eftersom resistansen hos ledaren inte är exakt 0.
Det var inte så jag tänkte... jag tycker jag har varit måttligt tydlig men ska göra ett till försök.
- Anta att resistansen i en kabel är exakt 0. Strunta i om det praktiskt sett vore omöjligt, bara låt det vara så.
- Anta nu att vi har en väldigt enkel krets där kabeln går från pluspolen i ett 3V-batteri till minuspolen i samma batteri.
- På vägen finns ingen resistor och ingen annan pryl heller. Det finns bara en kabel som är ansluten till ett 3V-batteri.
- Vi sätter på strömmen och då flödar strömmen från den positiva änden i 3V-batteriet till den negativa änden.
- Min fråga är följande. Bör det totala potentialfallet inte vara 3V? Från början har ju strömmen potentialen 3V. Potential är energi per laddning. När batteriets minuspol har utfört en kraft på laddningarna och dragit de en viss sträcka längs ledaren, då har ju en viss potentiell energi övergått till rörelseenergi. Alltså sjunker potentialen längs ledaren. Till slut i kretsen bör potentialen vara helt förlorad = 0 V. Tydligen är detta fel. Jag ber nu att du pekar ut varför jag har fel.
- Jämförelsevis kan vi ta homogena elektriska fält som exempel. Om en plusladdning sitter och nuddar vid den plusladdade plattan kommer laddningen ha en viss potential. Detta då plusladdningen känner en kraft i riktningen till den minusladdade plattan. Alltså, när plusladdningen närmar sig minusplattan, kommer denna laddningen få sänkt potential.
- Likadan princip borde kunna tillämpas på kretsar: att när strömmen närmar sig batteriets minussida kommer potentialen sjunka.
Låt mig snälla ha annat att tänka på under lovet än detta. Snälla hjälp mig bli klar i huvudet redan nu. :)
Du kanske redan har fått svar på dina frågor, men jag gör ett försök. Jo, såklart är det så att potentialen minskar utefter ledaren ju närmare minuspolen man kommer. Precis som exemplet med det homogena elektriska fältet. Vi kan räkna med ändliga värden istället, annars slår det lätt knut i huvudet...
Antag att du har en resistans på i ledaren, och på batteriet. Då skulle du få en strömstyrka på i ledaren, och om du hade en voltmeter att mäta potentialen mellan punkter utefter ledaren och minuspolen på batteriet så skulle du kunna mäta upp succesivt mindre spänningsfall ju närmare du mätte minuspolen. (Förutsatt att resistansen per längdenhet i ledaren är konstant, så att det elektriska fältet i ledaren blir homogent).
Men i praktiken kommer ditt experiment att misslyckas, av flera orsaker:
- Antag att du har ett litet batteri med inre resistans på . Den kan leverera max ström, sedan finns ingen polspänning kvar att driva mer ström genom ledaren. Dvs potentialen kommer inte att sjunka utefter ledaren eftersom potentialen redan är noll på batteriets pluspol. Batteriet är kortslutet.
Men om vi bortser från batteriets inre resistansen då?
- Antag att du har ett litet batteri med laddning. Du skulle ladda ur batteriet på och har svårt att hinna med att mäta potentialen utefter ledaren.
Men om vi bortser från batteriets kapacitet då?
- Effektutvecklingen i ledaren kommer att bli , och hela din mätuppställning skulle ögonblickligen brinna upp före du hann mäta. Om du hade tur så hade ledaren brunnit av som en säkring, och resten av mätupställningen klarat sig. (Då hade du kunnat mäta potentialen på ledarlängden före ledaravbrottet, och på ledarlängden efter ledaravbrottet.
Angående din ursprungsfråga i trådstarten, varför all batterispänning hamnar över resistorn och inte över anslutningsledarna.
Batteriet kommer att driva en ström av laddningar i den slutna kretsen som utgörs av anslutningsledare och resistor. Man antar att både anslutningsledare och resistor är ”ledare”, dvs dom leder ström och inga laddningar ansamlas någonstans (förutom i batteriet). Det betyder att drifthastigheten på elektronerna måste vara lika stor överallt i den slutna strömkretsen.
Drifthastigheten skapas av ett framdrivande elektriskt fält från batteriet, och tillsammans med friktionen (resistansen) som verkar i motsatt riktning skapas ett kraftjämviktsläge på laddningarna vid en viss drifthastighet, dvs en konstant ström, enligt Ohm’s lag. (Om ingen friktion funnits så skulle ju laddningarna istället accelerera).
För att åstadkomma samma drifthastighet på laddningarna (elektriskt ström) i hela kretsen så krävs olika stort elektriskt fält på olika ställen i kretsen. Det elektriska fältet blir alltså mycket större i resistorn än i anslutningsledare. Därför blir också potentialskillnaden mycket högre över resistorn än över anslutningsledarna. Och i normala fall när anslutningsledare har mycket mycket lägre resistans än resistorn, så kommer hela batterispänningen att hamna över resistorn.
Jag tror nyckelordet är laddningsfördelning, dvs att inga laddningar ansamlas någonstans, utan att samma ström av laddningar måste gå genom hela kretsen.
Jag uppskattar verkligen all hjälp, men tycker det har blivit för mycket på en gång. Jag har inte fått min fråga besvarad på ett sätt som jag kan förstå.
Just nu är det en enda sak, och inget annat, som jag vill kunna förstå. Hoppas det blir tydligare nu.
Here goes...
I en krets omvandlas potentiell energi hos elektronerna till kinetisk energi som i sin tur omvandlas till värme. Detta är logiskt och jag förstår det
Vad jag kämpar med att förstå är hur minskningen av potentiell energi sker så abrupt mellan ändarna i en resistor. Potentialen bör enligt mig falla successivt. Potentialen bör ju successivt övergå till kinetisk energi i kretsen.
Likställ detta med till exempel vatten. Föreställ er en stor konformad tratt fylld med vatten upp till kanten. Ner från tratten går ett smalt rör. Röret är "trångt" och ska symbolisera en resistor.
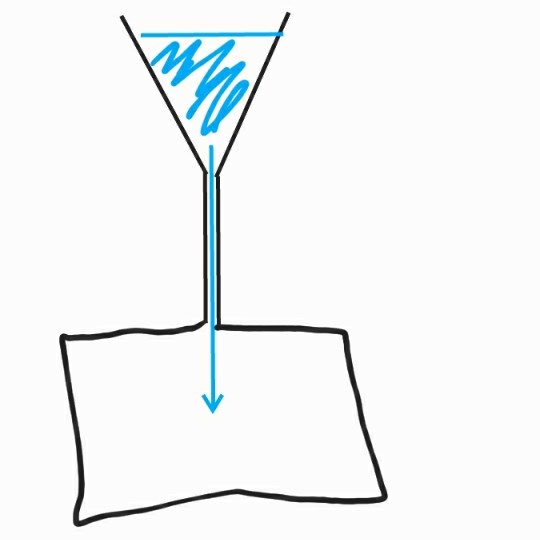
Från början har vattnet potentialla energin X. Men bara för det, kommer inte förlusten av potentiell energi förbi rörets ändar också vara X. Utan, som sagt, den potentiella energin bör sjunka successivt (i detta fall ju närmare vattnet kommer nollnivån. Alltså inte i en resistors ändar.)
Potentialfallet längs röret kommer inte utmärka sig från potentialfallet längs resten av anordningen, eftersom vattnet förlorar höjd SUCCESSIVT i hela systemet. Röret kommer enbart påverka (vatten)strömmen, så vattnet strömmar långsammare.
JohanF skrev:
För att åstadkomma samma drifthastighet på laddningarna (elektriskt ström) i hela kretsen så krävs olika stort elektriskt fält på olika ställen i kretsen. Det elektriska fältet blir alltså mycket större i resistorn än i anslutningsledare. Därför blir också potentialskillnaden mycket högre över resistorn än över anslutningsledarna. Och i normala fall när anslutningsledare har mycket mycket lägre resistans än resistorn, så kommer hela batterispänningen att hamna över resistorn.
Det som JohanF skriver här är egentligen svaret på din fråga Stenenbert men jag kan ge det ett försök.
Stenenbert skrev:Vad jag kämpar med att förstå är hur minskningen av potentiell energi sker så abrupt mellan ändarna i en resistor. Potentialen bör enligt mig falla successivt. Potentialen bör ju successivt övergå till kinetisk energi i kretsen.
En resistor är inte en magisk mojäng där det sker ett abrupt spänningsfall mellan ändarna. Den enklaste utformningen är en där man lindat en väldigt lång ledare med låg men faktisk resistans kring en insulerande keramisk kärna. Detta innebär att du självklart har ett successivt spänningsfall inuti resistorn men den idealiserade modellen som vi använder oss av beskriver förenklade komponenter. I denna modell beskriver vi en resistor som en magisk låda med plötsligt spänningsfall. Det finns en ocean av saker som försummas i denna modell (exempelvis att resistorer har parasiterande kapacitans).
Likställ detta med till exempel vatten. Föreställ er en stor konformad tratt fylld med vatten upp till kanten. Ner från tratten går ett smalt rör. Röret är "trångt" och ska symbolisera en resistor.
Du ska ha en eloge för att du försöker formulera ett pedagogiskt exempel. Du har varit väldigt tillmötesgående i denna tråd. Men, Ett batteri jämförs hellre med en vattenpump och den elektriska potentialen med trycket hos vattnet som flödar. Kolla den här länken och se om du förstår skillnaden mellan det du beskriver och den faktiska vatten-analogin:
Ha i åtanke att denna analogi egentligen är ganska problematisk då likheten mellan de fysikaliska systemen försvinner så snart du analyserar detaljer. Ännu värre är att om du har en växelströmskrets kan analogin orsaka stora problem för din intuition då det knappt finns någon överförbarhet.
Du gör analogin med det homogena E-fältet mellan två parallella plattor, där potentialen ökar (eller minskar, beroende på åt vilket håll man går) linjärt med avståndet. Men batteriets krets har inte ett homogent E-fält. Det är istället homogent ”i bitar”. Fältet är homogent/svagt i anslutningsledarna och homogent/starkt i resistorn. Och anledningen till att fältet fördelas på det viset utefter kretsen, är pga att jämvikten i laddningsfördelning måste till varje pris upprätthållas (dvs lika stor ström av laddningar genom varje tvärsnitt av kretsen, oavsett om tvärsnittet ligger i en anslutningsledare eller om tvärsnittettet ligger mitt genom resistorn), och strömmen blir då den styrande parametern som E-fältet måste rätta sig efter.
E-fältet måste helt enkelt bli större i resistorn för att kunna ”trycka igenom” samma mängd laddning per tidsenhet som i anslutningsledarna. Jämför analogin med vattentrycket som Ebola postade.
För att kunna förstå hur laddningsfördelningen skapar E-fältsfördelningen kan det kanske vara enklare att för ett ögonblick föreställa sig E-fältet som en konsekvens av den konstanta strömmen, även fast såklart strömmen överhuvudtaget inte uppkommer före man lagt på E-fältet. Men det är viktigt att förstå att det finns ett samspel (självreglerande återkoppling) mellan storheterna.
Tack för att ni försöker! Det känns bara som att en enda pusselbit fattas för att jag ska kunna ha ett okej grepp om spänningsfallet över resistorer. Du JohanF skrev detta:
Fältet är homogent/svagt i anslutningsledarna och homogent/starkt i resistorn. Och anledningen till att fältet fördelas på det viset utefter kretsen, är pga att jämvikten i laddningsfördelning måste till varje pris upprätthållas (dvs lika stor ström av laddningar genom varje tvärsnitt av kretsen, oavsett om tvärsnittet ligger i en anslutningsledare eller om tvärsnittettet ligger mitt genom resistorn), och strömmen blir då den styrande parametern som E-fältet måste rätta sig efter.
Hoppas det inte är för mycket begärt att fråga om varför jämvikt i laddningsfördelning till varje pris ska upprätthållas. Du skrev tidigare att detta ledde till en konstant och likadan hastighet (= drifthastigheten) i hela kretsen. Men varför är just konstant och jämn hastighet det enda alternativet? Varför måste detta upprätthållas? Finns det inte fall där laddningarna i en krets accelererar ( förutsatt att accelerationen är lika i hela kretsen)?
Jag nöjer mig även utan svar om detta inte är något enkelt att svara på. I vilket fall, detta lär bli min sista fråga. Tack så mycket återigen för att ni har försökt. :)
Oj, oj, oj vilka frågor! (Och jag visste att du skulle ställa dem, för det skulle jag ha ställt dem om jag hade varit i ditt ställe…).
Jag vet faktiskt inte om man kan använda klassisk fysik för att gå till botten med detta (eller så långt man kan gå...). Coloumbs lag om elektrostatiska krafter mellan laddningar kan nog förklaras lika lätt (dvs svårt…) som gravitationen kan förklaras.
Den konstanta drifthastigheten för laddningarna följer av Ohms lag , som är experimentellt framtagen och gäller bara ”för det mesta”. Laddningsjämvikten ställer in sig helt enkelt därför den kan, systemet strävar mot jämvikt enligt termodynamiska naturlagar. Materialet måste alltså vara av typen ”ledare” där det finns fria laddningsbärare tillgängligt. I ett sådant fall kommer alltid laddningsjämvikt att inträda, förr eller senare.
Men det finns fall där jämvikten varken kan ställa in sig förr eller senare och Ohms lag får stora problem. När man börjar observera och räkna på snabba signaler och snabba förlopp (tex AC med höga signalfrekvenser, istället för DC), och/eller när den fysiska längden på ledarna är ”långa i förhållande till tidsförloppen”. Fenomenet som inträffar är att laddningarna helt enkelt inte hinner ställa in sig i jämvikt innan det drivande E-fältet har hunnit vända riktning. Då måste man använda differentialekvationer för att förklara och beräkna hur ström och spänning fördelas längs ledare, istället för ohms lag, se https://en.wikipedia.org/wiki/Transmission_line#Telegrapher's_equations , och man får lösningar som får våg-liknande beteende. Det är till exempel därför som man måste räkna på ledningslängder och impedanser när man gör snabba databussar i datorer, annars riskerar man, precis som dina frågor delvis handlat om, att få områden på en anslutningsledare där spänning och ström helt enkelt ”tar slut” (så kallade stående vågor, med periodiskt återkommande minima och maxima, som du kommer att räkna på när ni läser om ljusvågor). Jag jobbar själv en del med sådana fenomen, och kom ihåg hur förvånad jag blev när jag stötte på dem för första gången i helt oväntade sammanhang.
Men så länge man pratar om ledare och andra elektriska komponenter där komponenterna beskrivs som diskreta element så ska du utan tvekan använda Ohms lag.
Jag försöker jättegärna svara på dina frågor, så var inte orolig för att fråga. Däremot tycker jag att du ska ställa dina kvalificerade funderingar i andra forum också, och till din fysiklärare, så att du får fler synvinklar. För rätt som det är så börjar någon omedvetet svamla och förklara fel. Den här kommer du att få kvalificerade svar ifrån, http://fragelada.fysik.org/
Hej
Vill bara stämma in i hyllningskören. Jag beundrar din envishet att vilja förstå.
Ibland får man godta att saker är som de är utan att helt och fullt förstå hur man kom dit.
En berömd engelsk 1600-tals fysiker lär ha sagt: "If I have seen further it is by standing on the shoulders of Giants."
Hälsningar
Thomas





