Spänning mellan P och Q
Hej! Jag förstår inte exakt varför man tar enbart spänning för 60 subtraherat med spänningen 12v för att få ut spänningen mellan P och Q
Kan någon förklara varför man gör så jag har svårt att förstå det
Du har ju hållit på med potentialvandring, så prova det.
Gå från batteriets minuspol, mot strömmen, som jag ritat:
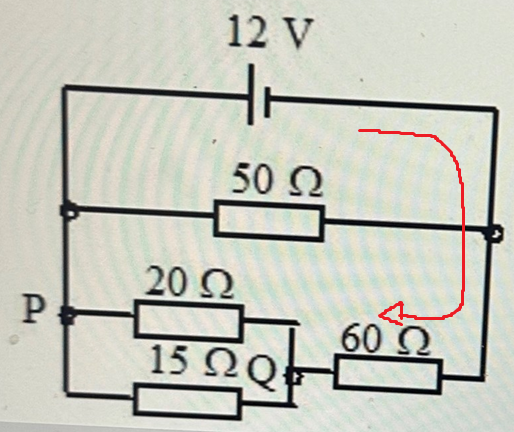
Vad får du då för spänning i Q?
Vilken spänning vet du att du har i P?
Jaha, vi har 12 v för P
och Q räknar jag som 12-15*0,175 = 9,375 v
men så de tar spänningen för p och subtraherar det med spänning för 60 för att få den spänning mellan de som är Q? Eller nu är jag lite Borta
R.zz skrev:Jaha, vi har 12 v för P
och Q räknar jag som 12-15*0,175 = 9,375 v
men så de tar spänningen för p och subtraherar det med spänning för 60 för att få den spänning mellan de som är Q? Eller nu är jag lite Borta
Nu tappade du resistorn som är 20 Ω. Vill du gå från P till Q så måste du beräkna ersättningsresistansen för parallellkopplingen.
Det var dock inte vad du frågade och heller inte vad jag bad dig göra.
Genom 60 Ω flyter strömmen 175 mA. Spänningen över resistorn är då 10,5 V.
Vi vandrar mot strömmen, så spänningen kommer att öka med varje resistor.
Vid minuspolen är spänningen 0 V, i det blå området.
Vi räknade ut att det ligger 10,5 V över 60 Ω.
Spänningen i Q är då 0+10,5=10,5 V.
Sedan kan vi räkna ut ersättningsresistansen för 20 Ω || 15 Ω, men det behöver vi inte.
Om vi fortsätter vandra genom dem kommer vi till det röda, där vi vet att spänningen är 12 V.
Då måste spänningen mellan P och Q vara P-Q=12-10,5=1,5 V.
Sedan kan vi ju roa oss med att kontrollera detta.
Eftersom vi nu vet att spänningen över 20 Ω || 15 Ω är 1,5 V och vi dessutom vet att strömmen genom dem är 175 mA så kan vi räkna ut vad ersättningsresistansen måste vara.
Ohms lag: 1,5=0,175R ger R≈8,6 Ω.
Vi räknar även på parallellkopplingen: 1/(1/20+1/15)≈8,6 Ω.
Ahaaa tack så mycket nu förstår jag !
