Spåravstånd Cd-skiva

Standardfråga 1a: Har du ritat?

Smaragdalena skrev:

Standardfråga 1a: Har du ritat?

 Nej.. är helt förvirrad och vet inte ens vart jag ska börja..

någon?

Visst är spåren cirkulära med en radie på kanske 4 cm - 7 cm, men du kan i en första (och ganska bra) approximation se CD:n som ett plant reflexionsgitter.

hjalpmedfysik skrev:

någon?

 hjalpmedfysik, det står i Pluggakutens regler att du behöver vänta åtminstone 24 timmar innan du bumpar din tråd. 15 timmar fär för lite. /moderator

någon?

Läs svaret från Dr G igen.

Bubo skrev:

Läs svaret från Dr G igen.

 Ja men förstår fortfarande inte vad jag ska göra. Är det bara gitterekvationen jag ska använda? 

Vad får du om du använder gitterekvationen?

Osäkerheterna kan du ta i nästa steg.

Dr. G skrev:

Vad får du om du använder gitterekvationen?

Osäkerheterna kan du ta i nästa steg.

gitterformel: n*λ = d*sin(An)

λ = våglängd (650-670)

n = ordningsnummer (1)

d = gitterkonstant (d = nλ/sin(An))

An = vinkel

avstånd mellan central och första ordningens maximum = 44,2/2 = 22,1cm

Så först måste jag ta reda på d = 1*λ/Sin(An), men vilken våglängd är det jag ska ta eftersom det är 650-670, och hur hittar jag vinkeln?

Om du ritar figur så kan du se att du vet tangens för vinkeln.

I brist på mer info så kan du ta λ ≈ 660 mm.

Dr. G skrev:

Om du ritar figur så kan du se att du vet tangens för vinkeln.

I brist på mer info så kan du ta λ ≈ 660 mm.

 Ska jag då rita av själva CD skivan, tavlan, laserpekaren och markera ut första ordnings & centralmaximum?

Ja, det låter bra. 

Dr. G skrev:

Ja, det låter bra. 

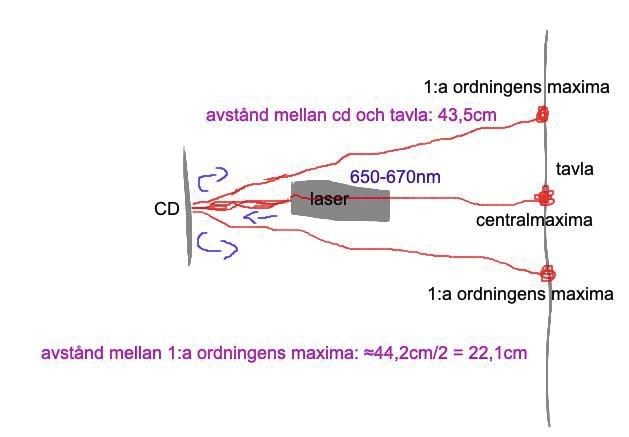
Ser du två rätvinkliga trianglar i din bild?

Hur stora är vinklarna?

Dr. G skrev:

Ser du två rätvinkliga trianglar i din bild?

Hur stora är vinklarna?

 trianglarna är alltså punkterna från CD/1:a/centralmaxima,  så 90 grader??

gitterkonstant: d = n*våglängd/sin(vinkel)

1*650/sin(90) ≈ 727nm

1*670/sin(90) ≈ 749nm

första våglängden: (n*våglängd)/d)sin^(-1)

(1*650)/727)sin^(-1) ≈ -0,75

(1*670/749)sin^(-1) ≈ -0,775

Är jag på rätt väg eller är jag helt ute och cyklar??

(sinus för) vinkeln som ska in i gitterekvationen är den som jag markerar med v i din figur.

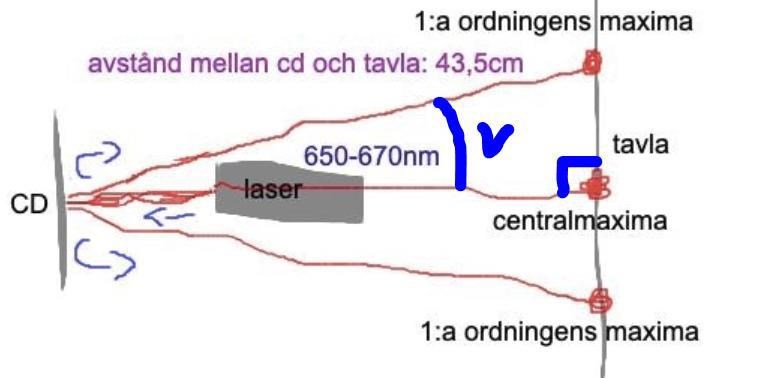
Enklast är kanske att beräkna v om du kan hitta ett uttryck för tan(v).  Annars går det bra att ta fram sin(v) direkt m.h.a Pythagoras.

Dr. G skrev:

(sinus för) vinkeln som ska in i gitterekvationen är den som jag markerar med v i din figur.

Enklast är kanske att beräkna v om du kan hitta ett uttryck för tan(v).  Annars går det bra att ta fram sin(v) direkt m.h.a Pythagoras.

 Blir tan(v)  då = 43,5/22,1 ≈ 1,96?

Nej, hur är tan(v) definierat i en rätvinklig triangel?

Dr. G skrev:

Nej, hur är tan(v) definierat i en rätvinklig triangel?

 För en rätvinklig triangel definieras de trigonometriska funktionerna enligt följande:

tan(v) = motstående katet/närliggande katet

alltså: 22,1/44,2 = 0,5. Blandade ihop motstående/närliggande

Så 

tan(v) = 22.1/43.5

Du behöver sin(v). sin(v) kan du ta direkt från geometrin ovan m.h.a Pythagoras, eller så kan du med miniräknare räkna ut v och sedan sin(v).

Dr. G skrev:

Så 

tan(v) = 22.1/43.5

Du behöver sin(v). sin(v) kan du ta direkt från geometrin ovan m.h.a Pythagoras, eller så kan du med miniräknare räkna ut v och sedan sin(v).

 just ja 43,5 och inte 44,2 hahah

hypotenusan: 43,5^2+22,1^2 = 2380,66, rotenur2380,66 ≈ 48,79cm

sin(v) = 22,1/48,79 ≈ 0,45

Precis.

Vad blir då avståndet mellan spåren?

Dr. G skrev:

Precis.

Vad blir då avståndet mellan spåren?

gitterekvationen är ju n*våglängd=d*sin(vinkel), men hur gör jag om formeln?

sen så har jag 2 våglängder 650-670, vilken ska jag använda? 

Kan du lösa ut d?

Våglängden är någonstans mellan 650 mm och 670 mm. Välj först en våglängd mitt i intervallet.

För osäkerheterna kan du välja värden på dina parametrar i intervallen så att d blir så liten eller så stor som möjligt.

Dr. G skrev:

Kan du lösa ut d?

Våglängden är någonstans mellan 650 mm och 670 mm. Välj först en våglängd mitt i intervallet.

För osäkerheterna kan du välja värden på dina parametrar i intervallen så att d blir så liten eller så stor som möjligt.

 d = n*våglängd/sin(alpha) = 1*660(om jag väljer våglängden mitt i intervallet)/sin(0,45) = 1517,3616028. Men ska gitterkonstanten inte vara x*10^(x)?

Du har fått fram att

sin(v) ≈ 0.45

Du ska inte ta sin(0.45).

$d = n\lambda/\sin(v) = ...$

Dr. G skrev:

Du har fått fram att

sin(v) ≈ 0.45

Du ska inte ta sin(0.45).

$d = n\lambda/\sin(v) = ...$

 Men om jag isåfall tar d = 1*660/0,45 = 1466,66667...

Om du inte avrundar sin(v) ≈ 0.45 så får du c:a 

1457

Vad är det för enhet?

Dr. G skrev:

Om du inte avrundar sin(v) ≈ 0.45 så får du c:a 

1457

Vad är det för enhet?

1467nm? 

Ja.

Hur ska du göra med osäkerheterna i våglängd och vinkel?

Dr. G skrev:

Ja.

Hur ska du göra med osäkerheterna i våglängd och vinkel?

 Osäkerheterna för avståndet har jag skrivit som +/-2mm, jag vet dock inte hur jag ska skriva när det kommer till våglängd och vinkel?

Med n= 1 har du att

$d=\lambda/\sin(v)$

Det största värdet på d får du när lambda är som störst (i det givna intervallet) och sin(v) är som minst (i det givna intervallet). 

Vilka värden på lambda och dina sträckor ska du använda för att få d så stor som möjligt?

Dr. G skrev:

Med n= 1 har du att

$d=\lambda/\sin(v)$

Det största värdet på d får du när lambda är som störst (i det givna intervallet) och sin(v) är som minst (i det givna intervallet). 

Vilka värden på lambda och dina sträckor ska du använda för att få d så stor som möjligt?

 lambda blir då 670, men sträckor/sin(v) är väl 0,45 oavsett?

Jag har väl redan fått reda på svaret på frågan eftersom gitterkonstanten = spårlängden, eller??

Du har inte ett exakt värde på vinkeln v - vilket värde har den som mest respektive som minst?

Smaragdalena skrev:

Du har inte ett exakt värde på vinkeln v - vilket värde har den som mest respektive som minst?

 Hur ska jag göra för att få ut de två värdena då? jag tog ju 

hypotenusan: 43,5^2+22,1^2 = 2380,66, rotenur2380,66 ≈ 48,79cm

sin(v) = 22,1/48,79 ≈ 0,45

Vilka andra värden är det jag ska räkna med?

Du har längden på de båda kateterna (med felmarginaler). Vilken är den största respektive minsta vinkeln de kan ge upphov till? Använd dig av arc tangens-funktionen.

Smaragdalena skrev:

Du har längden på de båda kateterna (med felmarginaler). Vilken är den största respektive minsta vinkeln de kan ge upphov till? Använd dig av arc tangens-funktionen.

 menar du +/-2mm? 

(+2mm): 43,7^2+22,35^2 = 2497,61, rotenur2497,61 ≈ 49,97

sin(v) = 22,35/49,97 ≈ 0,44

(-2mm): 43,3^2+21,9^2 = 2354,5, rotenur2354,5 ≈ 48,52

sin(v) = 21,9/48,52 ≈ 0,45

??

Har du testat de båda andra kombinationerna också?

(sinus för) vinkeln blir så stor som möjligt om kateten är lång och hypotenusan är kort. 

Kateten är som längst (44.2 + 0.2)/2 cm.

Hypotenusan är som minst när den andra kateten är (43.5 - 0.2) cm.

(Avrunda inte sin(v) till två decimaler i det här skedet.)

Dr. G skrev:

(sinus för) vinkeln blir så stor som möjligt om kateten är lång och hypotenusan är kort. 

Kateten är som längst (44.2 + 0.2)/2 cm.

Hypotenusan är som minst när den andra kateten är (43.5 - 0.2) cm.

(Avrunda inte sin(v) till två decimaler i det här skedet.)

kateten: (44,2+0,2)/2 = 22,2cm

hypotenusan: 43,5-0,2 = 43,3cm

sin(v) som störst = 22,2/43,3 = 0,511521

----

ska jag ta +0,2 på hypotenusan för att få ut sin(v) som minst?

kateten: (44,2-0,2)/2 = 22cm

hypotenusan: 43,5+0,2 = 43,7cm

sin(v) som minst = 0,503432

Du verkar nu räkna ut tan(v).

Dr. G skrev:

Du verkar nu räkna ut tan(v).

 Ja, och när du har tagit reda på vinkeln $v$ kan du beräkna $\sin \left(v\right)$.

Dr. G skrev:

Du verkar nu räkna ut tan(v).

 Förlåt men jag är helt förvirrad..

Du delar den ena kateten på den andra, inte på hypotenusan, eller hur? (och får därav tangens och inte sinus).