Speciell relativitet - rörelsemängd. Kolliderande partiklar.

Hej

Detta är min uppgift: 

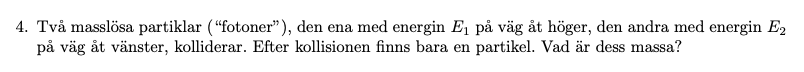
Min föreläsares vackra men kryptiska lösning är: 

Vill någon förklara hur han tänker?

En annan metod, som min föreläsares metod säkert bygger på, eller tvärtom är: 

Låt c=1 och positiv riktning åt höger.

Vet att: 

$E_{tot}^2-(pc)^2=(mc^2)^2$ (1)

För båda masslösa partiklar har vi då att:

$E_1 = |p_1| = p_1$ (den åker åt höger) och

$E_2 = |p_2| = -p_2$ (den åker åt vänster).

Sätt in i (1) där både rörelsemängd och energi är bevarat. Vi får då: 

$m=2\sqrt{E_1E_2}$, vilket är rätt. Är detta en korrekt metod? Är det korrekt att bestämma tecken på rörelsemängden efter absolutbeloppet? Eller går det att sätta in minus någonstans tidigare och använda den skumma skalärprodukten med ett minustecken..?