Spegelbild av en punkt
Hej, jag undrar om min metod fungerar att använda samt om det finns andra sätt att lösa uppgiften på.
Frågan lyder såhär:
Jag ritade bilden: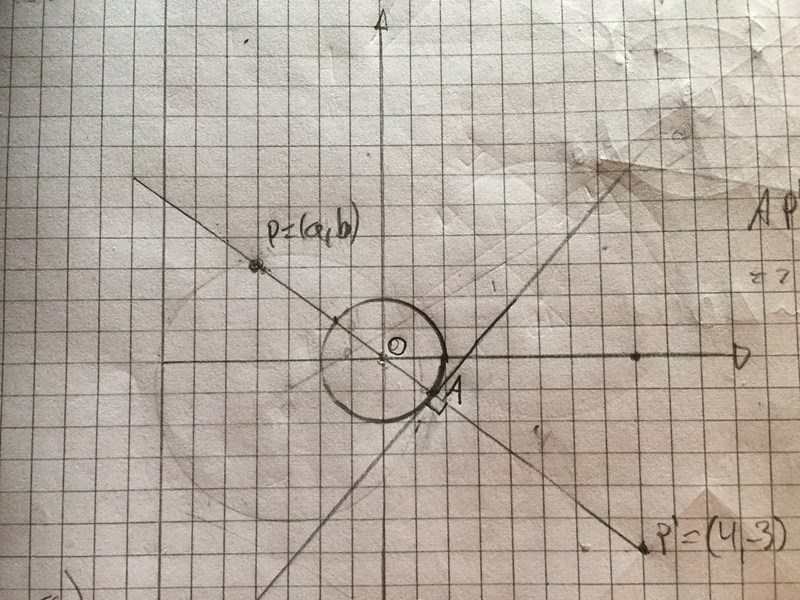
När det gäller spegling så vet vi att |P'A|=|PA|, vi kan även beräkna |OP'| mha pythagoras sats och får att |OP'|=. Då vi har en enhetscirkel med r= 1 så får vi att |AP'|=5-1=4. På liknande sätt får vi då att |PO|=4-1=3, om vi kallar punkten P koordinater för (x,y) ( och inte (a,b) som i bilden) så får jag att:
|PO|=3=
Då de två punkterna P' och P ligger på samma linje så kan vi även beräkna linjens ekvation som blir y=
Vi får då ekvationssystemet:
Löser vi detta så får vi att x=2,4 samt att y=1,8, stämmer detta?
Kan du rita en bild där mar ser att infallsvinkeln är lika med reflektionsvinkeln?
Vad betyder det att spegla i en cirkel? Analogt med att spegla sig i en metallkula? Det första jag tänkte på var en Möbius-transform, men det kan det ju inte handla om här.
Ekvationssystemet stämmer, men x blir -2,4
Smaragdalena skrev:Kan du rita en bild där mar ser att infallsvinkeln är lika med reflektionsvinkeln?
Vi har inte jobbat med infalls respektive reflektionsvinklar, så tror inte att vi ska använda det för att lösa problemet
Laguna skrev:Vad betyder det att spegla i en cirkel? Analogt med att spegla sig i en metallkula? Det första jag tänkte på var en Möbius-transform, men det kan det ju inte handla om här.
Det är ingenting som vi har gått igenom men vår lärare tyckte att vi skulle kunna lösa denna uppgift med hjälp av några ledtrådar ( se bifogad bild) samt med hjälp av det som vi lärt oss i kursen
det står dock en del om det här: https://en.wikipedia.org/wiki/Inversive_geometry
larsolof skrev:Ekvationssystemet stämmer, men x blir -2,4
Tack så mycket det blev ett slarvfel :D
Krasten skrev:
Det är ingenting som vi har gått igenom men vår lärare tyckte att vi skulle kunna lösa denna uppgift med hjälp av några ledtrådar ( se bifogad bild) samt med hjälp av det som vi lärt oss i kursen
det står dock en del om det här: https://en.wikipedia.org/wiki/Inversive_geometry
Om det är detta som innebär spegling i cirkel så stämmer inte din uträkning.
Det står att punkterna ligger på samma stråle, vilket innebär att båda punkterna ligger i fjärde kvadranten.
Det står att , men du har tolkat det som att .
Den punkt som uppfyller villkoren, dvs spegelbilden, är istället (1/5, -3/20).
Är detta verkligen Ma2? Vilken bok använder ni? /moderator
Smaragdalena skrev:Är detta verkligen Ma2? Vilken bok använder ni? /moderator
Om villkoren ovan är givna så borde uppgiften gå att lösa med kunskaper från Matte 2.
Det enda som behövs är att veta vad en stråle är samt hur man beräknar en vektors längd.
Yngve skrev:Krasten skrev:Det är ingenting som vi har gått igenom men vår lärare tyckte att vi skulle kunna lösa denna uppgift med hjälp av några ledtrådar ( se bifogad bild) samt med hjälp av det som vi lärt oss i kursen
det står dock en del om det här: https://en.wikipedia.org/wiki/Inversive_geometryOm det är detta som innebär spegling i cirkel så stämmer inte din uträkning.
Det står att punkterna ligger på samma stråle, vilket innebär att båda punkterna ligger i fjärde kvadranten.
Det står att , men du har tolkat det som att .
Den punkt som uppfyller villkoren, dvs spegelbilden, är istället (1/5, -3/20).
Stämmer (1/5, -3/20) ?
|OP'| är väl = 5 och r=1
då blir väl |OP| = 1/5 ?
Med (1/5, -3/20) blir |OP| = 1/4
larsolof skrev:
Stämmer (1/5, -3/20) ?|OP'| är väl = 5 och r=1
då blir väl |OP| = 1/5 ?
Med (1/5, -3/20) blir |OP| = 1/4
Tack larsolof, det var slarvigt av mig.
Det stämmer att det är |OP| och inte x-koordinaten för P som är 1/5.
Vi får då att koordinaterna för den speglade punkten P är (4/25, -3/25).
Yngve skrev:Smaragdalena skrev:Är detta verkligen Ma2? Vilken bok använder ni? /moderator
Om villkoren ovan är givna så borde uppgiften gå att lösa med kunskaper från Matte 2.
Det enda som behövs är att veta vad en stråle är samt hur man beräknar en vektors längd.
Enhetscirkeln lär man sig i Ma3. Man pratar lite om vektorer i Ma1c. Spegling undrar jga om det finns i gymnasiekursen alls.
Smaragdalena skrev:
Enhetscirkeln lär man sig i Ma3. Man pratar lite om vektorer i Ma1c. Spegling undrar jga om det finns i gymnasiekursen alls.
Det behövs ingen kunskap om vare sig enhetscirkeln eller spegling för att lösa uppgiften.
Den cirkel som ska användas är tydligt beskriven, likaså vad spegling i en cirkel innebär.
Dessutom låter det som att detta är en "extrauppgift".





