Standardsubstitution
Vi fick tipsen att ersätta såhär när vi har en krångligt integral.
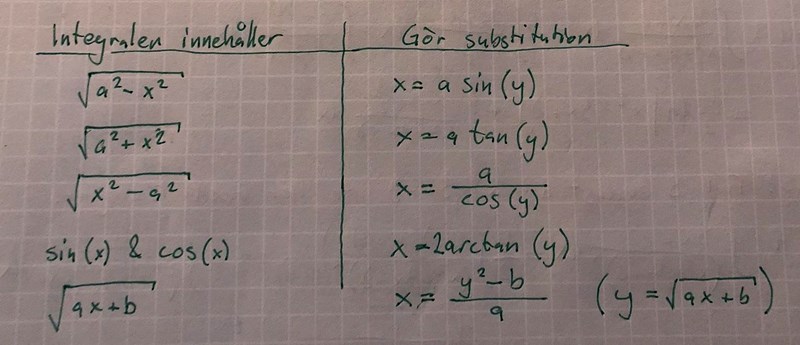
Grejen är... hur hanterar man dy/dx i variabelsubstitution?
Menar du vad man gör med i vid substitution?
Då nyttjar man kedjeregeln
och substituerar med det uttrycket man får vid . Differentialen man får kan alltså vara symboliskt ganska komplicerad om man har otur.
Men som alltid är det bra att utgå från några konkreta problem.
Här:
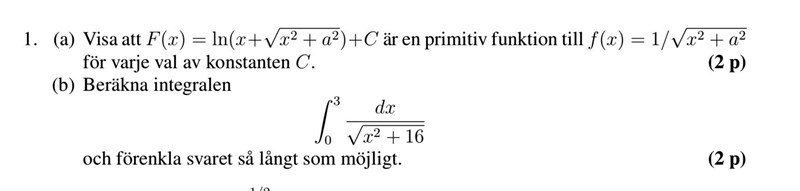
Hur kan man fixa dessa problem med substitutionen som ?
Varför vill du integrera talet med en substitution? Använd det du bevisat i a) för att hitta en primitiv till istället. :)
Det är inte det jag frågar om :)
Vad får du om du provar med x = a*tan(y)? dx = ...*dy
Du blir också av med rottecknet med
x = a*cosh(y)? dx = ...*dy
Prova båda!
Jag blir av med rottecken. Men däremot, jag blir "på" med en massa saker som jag kan inte vara av med.
(Herregud det var forfarligt grammatik)
Det är som den värsta skorv i ett litet barns huvud! Försök bara att borsta den bort, det är helt omöjligt!
Arabisk cos (cosh) har vi inte misshandlat så mycket i denna kurs, så jag vill gärna fatta först med tangent.
dajamanté skrev:Det är inte det jag frågar om :)
Om du låter så blir
och integralen kan skrivas
.
Trigonometriska ettan visar att
så att integralen är
.
Albiki skrev:dajamanté skrev:Det är inte det jag frågar om :)
Om du låter så blir
och integralen kan skrivas
.
Tack Albiki, försöker återkomma lite senare idag...
Albiki skrev:dajamanté skrev:Det är inte det jag frågar om :)
Om du låter så blir
Om , jag förstår inte varför ?
EDIT : Jag märkte att jag var nöjd med svaret av misstag!
Jag är jättenöjd mer era svar, men vi måste fortfarande klura ut den här!





