Statistik - väntevärde av funktion av S.V
Är förvirrad angående hur de väljer k i satsen och beviset. I beviset sätter dem g(X) = k, men i satsen 5.1 för diskreta fallet så har dem istället att X=k, vilket inte borde vara samma sak?

I beviset sätter dem g(X) = k
Nej, jag ser inte att de sätter g(X)=k. Kanske tänker du på detta:
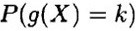
här kanske det ser ut som att de gör det som du säger, men uttrycket ska läsas som "sannolikheten för att g(X) är k". I nästa led kallar de denna sannolikhet för .
Jag tror att du förväxlar stokastiska variabler med "vanliga" variabler som t.ex. kan stå för ett reellt tal. En stokastisk variabel är mer komplicerad. Det är en funktion, se wikipedia. Man kan alltså inte heller säga, om en stokastisk variabel X, att X=k, där k är ett reellt tal. En stokastisk variabel är inte ett reellt tal.
Peter skrev:I beviset sätter dem g(X) = k
Nej, jag ser inte att de sätter g(X)=k. Kanske tänker du på detta:
här kanske det ser ut som att de gör det som du säger, men uttrycket ska läsas som "sannolikheten för att g(X) är k". I nästa led kallar de denna sannolikhet för .
Jag tror att du förväxlar stokastiska variabler med "vanliga" variabler som t.ex. kan stå för ett reellt tal. En stokastisk variabel är mer komplicerad. Det är en funktion, se wikipedia. Man kan alltså inte heller säga, om en stokastisk variabel X, att X=k, där k är ett reellt tal. En stokastisk variabel är inte ett reellt tal.
Så enligt boken definierar de sannolikhetsfunktionen av en diskret S.V som , där x=a1, a2, a3, ... etc är uppräkneligt många tänkbara värden som den S.V X kan anta.
Min förvirring kommer ifrån när jag jämför med i beviset.
Om man ska beskriva detta med ord verkar det som om man i sats 5.1 fokuserar på att addera ihop sannolikheterna dvs sannolikheterna då X antar värdena k multiplicerat med värdet g(k), medan i beviset i den inre summationen verkar man istället addera ihop sannolikheterna , men där j är sådant att g(j) = k uppfylls, och multiplicerar detta med g(j) = k.
För mig ser detta inte ut som om man lägger ihop samma saker så att säga. Den ena fokuserar på sannolikheterna P(X=k) medan den i beviset fokuserar på P(X=j) sådant att g(j) = k.
Jag förstår inte heller din kommentar helt och hur det påverkar min uppfattning. S.V är en reellvärd funktion som mappar från utfallsrummet till reella tallinjen, i fallen då utfallsrummet är just reella tallinjen blir S.V en identitetsfunktion antar jag (okej detta lär nog inte alltid stämma). Men i vilket fall, så har ju en funktion reella tal som den kan anta givet en input, talen den kan anta beskrivs väl av funktionens värdemängd.
bump
bump
Observera vad som först sägs i beviset, utan att skrivas med formler:
"Vi ordnar om termerna i högra ledet av den första formeln i Sats 5.1 och får genom att föra ihop alla med samma värde på g(k)".
Poängen är alltså att:
Det som är förvirrande här är att k inte betecknar samma sak i det två leden. I VL är k de värden X kan anta. I HL är j de värden X kan anta och k de värden som Y=g(X) kan anta. Det är inte förklarat på ett bra sätt i beviset. Men det är när vi väl förstått detta ett väldigt självklart samband. Vi klumpar ihop de termer i VL för vilka funktionen g antar samma värde.

