stokes sats

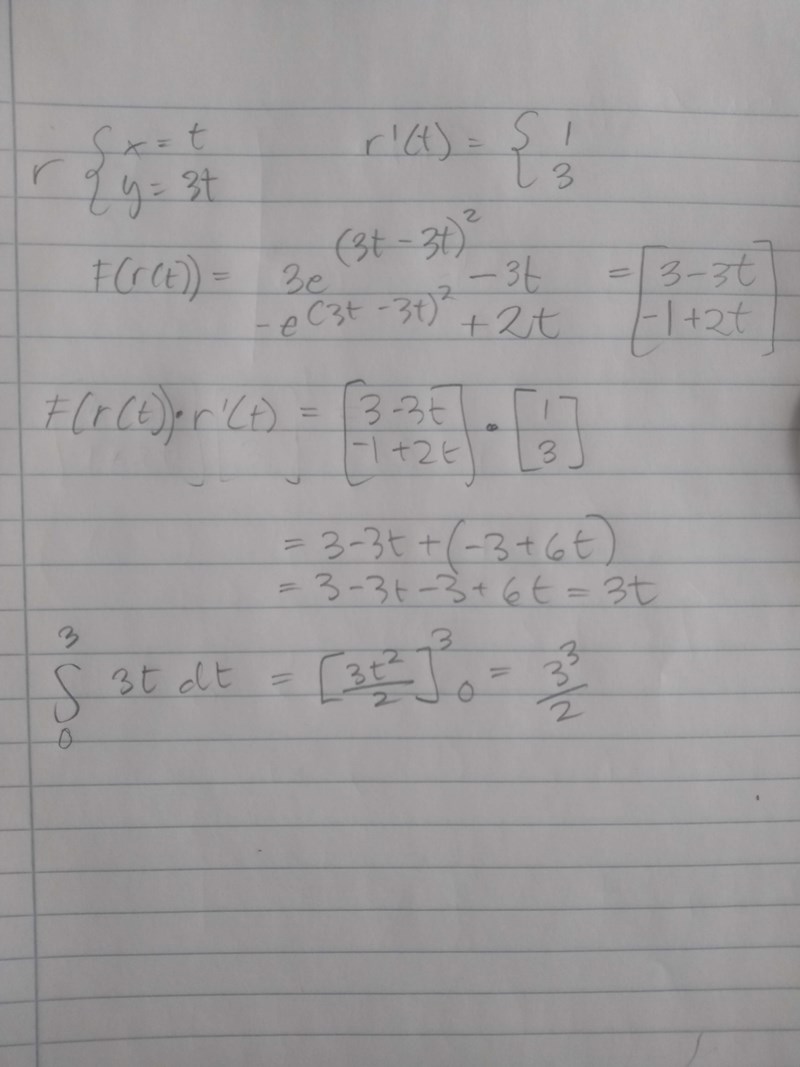
Varför har du valt just den parametriseringen?

Jag rekommenderar dig att kika på differensen:

$\dfrac{\partial Q}{\partial x}-\dfrac{\partial P}{\partial y}$

Om man beräknar denna differens får man ett enkelt uttryck, vilket kan tyda på att det kan vara klokt att använda en viss formel. Vet du vilken?

Hej. tydligen skall man ta integralen av det AlvinB's differens och mitt svar dvs 3^3/2. Jag förstår dock inte varför det skulle bli rätt för det

Du gör en parametrisering med en rät linje. Uppgiften anger dock att rörelsen sker längs en parabel. Du kan inte byta integrationsväg om ditt fält inte är ett potentialfält. Jag ser inte heller var du använder stokes sats, men det spelar ingen roll eftersom du inte kan använda stokes sats i 2 dimensioner(om du inte menar att du vill använda greens formel som ett specialfall av generaliserade stokes)

Jag har löst uppgiften men har inte riktigt förstått vad jag gjort eller varför. mitt svar är 27. jag förstår inte varför jag räknar ut två saker o sen adderar tsmns dom eller varför integrationsgärnsen för y är mellan x^2 och 3x på den ena integrationen. Här är mina uträkningar: 

Om du vill förstå vad du gör rekommenderar jag dig att noggrant läsa igenom formuleringen av Greens formel, eftersom det är den du använder. I detta fallet har du en parabel i planet du vill integrera över. För att kunna använda greens formel behöver du dock en sluten kurva så du sluter den med den räta linjen från (0,0) till (3,9) för att avgränsa ett område av planet. I y-led begränsas ju området nedåt av y=x^2 och uppåt av y=3x, därför blir det gränserna i din dubbelintegral.

Ja, nu är du på rätt spår. Vad vi använder oss av är Greens formel, som säger att en integral av en sluten kurva $C$ kan beräknas med dubbelintegralen:

$\displaystyle\oint_{C}P\ dx+Q\ dy=\iint_D\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\ dxdy$

Vi kan nästan applicera denna på vår kurva, förutom att den inte är sluten. Vi behöver därför lägga till ett linjestycke $\gamma_1$ mellan punkterna $(0,0)$ och $(3,9)$. Greens formel ger då:

$\displaystyle\int_\gamma P\ dx+Q\ dy-\int_{\gamma_1}P\ dx+Q\ dy=\iint_D\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\ dxdy$

(minustecknet framför $\gamma_1$-integralen kommer av att den genomlöps moturs med Greens formel, men vi har orienterat den medurs)

Med det du beräknat får vi då:

$\displaystyle\int_\gamma P\ dx+Q\ dy-\frac{27}{2}=\frac{27}{2}$

$\displaystyle\int_\gamma P\ dx+Q\ dy=\frac{27}{2}+\frac{27}{2}=27$

Blev det klarare då?

okej då hänger jag med tack! En liten följdfråga. skulle man kunna göra något sånt här liknande?

ifall $$integralen $$gick 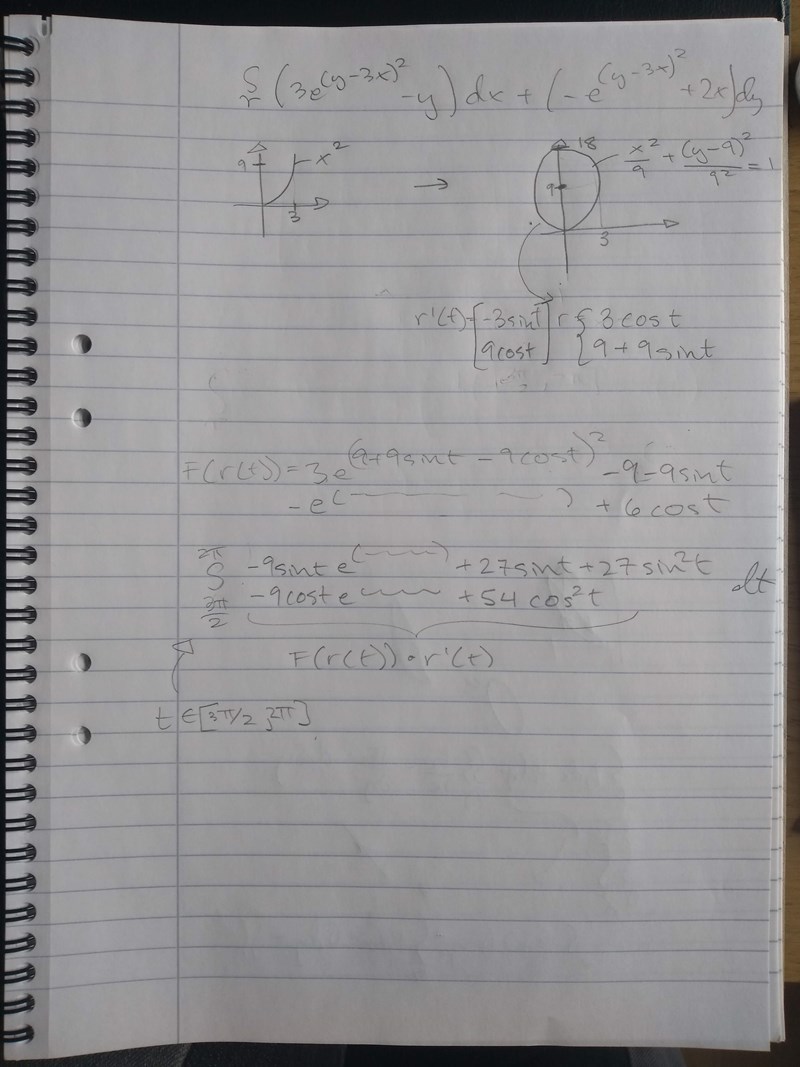$att lösa$

Nej, en parabel och en cirkel är inte samma sak. Den parametriseringen du skulle använda skulle isåfall vara r(t)=(t,t^2)