Stokes sats
Hur ska jag tänka om u har exponent tex u=(3z^2,5x^3,-2y^3) ist för som i uppg isf blir ju rotu=(-6y^2, 6z, 15x^2) ist för (-2, 3, 5) hur ska jag då tänka med variablerna x y z i rotu? Int rotuNdS= (15x^2-6z)pi 🤷♀️

Du vill alltså undersöka vad som händer ifall vi istället tar .
Enda skillnaden i så fall är att integranden inte blir konstant, men eftersom du tar en integral är det ju inget problem.
Visa oss hur du räknar när du kör fast.
AlvinB skrev:Du vill alltså undersöka vad som händer ifall vi istället tar .
Enda skillnaden i så fall är att integranden inte blir konstant, men eftersom du tar en integral är det ju inget problem.
Visa oss hur du räknar när du kör fast.
När jag läste ur boken så är ju integralen arean av ellipsen som uppstår (se bild) vilket gör att jag funderade på hur jag skulle gjort om u innehåller variabler som vid derivering för blev variabler tex som jag skrex exempel på.
Här är fortsättningen på bokens exempel:
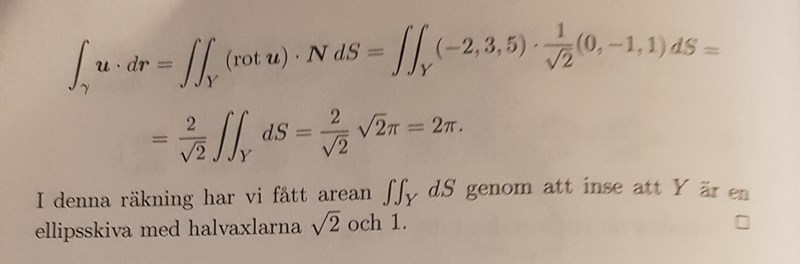
Ja, okej, facit använder ett fultrick för att slippa beräkna integralen. Men du kan ju fortfarande beräkna integralen på vanligt vis!
AlvinB skrev:Ja, okej, facit använder ett fultrick för att slippa beräkna integralen. Men du kan ju fortfarande beräkna integralen på vanligt vis!
Men hur gör jag då, när det blir en sned ellips?! Jag skulle vilja parametrisera, men de låser sig när det liksom är skärningen mellan en cylinder och ett plan 🤦
Jaha! Det är här problemet ligger.
Vi vill ju beräkna ytintegralen
När vi har är det inte så lätt, men vi kan omvandla det hela till att integrera över områdets projektion i -planet. Då blir integralen:
där normalen inte längre är en normerad normal, utan den ges av:
(Detaljerna om vad som egentligen händer här kan du förmodligen läsa om i din kursbok eller denna tråd. Fråga gärna mer också om det är något du inte förstår.)
Sätt nu in i det jag skrev ovan och se hur långt du kommer.
AlvinB skrev:Jaha! Det är här problemet ligger.
Vi vill ju beräkna ytintegralen
När vi har är det inte så lätt, men vi kan omvandla det hela till att integrera över områdets projektion i -planet. Då blir integralen:
där normalen inte längre är en normerad normal, utan den ges av:
(Detaljerna om vad som egentligen händer här kan du förmodligen läsa om i din kursbok eller denna tråd. Fråga gärna mer också om det är något du inte förstår.)
Sätt nu in i det jag skrev ovan och se hur långt du kommer.
Jag tror jag fattar vad du skriver men jag fattar inte hur jag ska göra när jag inte har en ekvation utan två för ytan 😥
Du skall ju parametrisera ytan, inte vektorfältet (?)!
Ytan är ju planet . Normalvektorn blir då:
Vad blir då integralen?
AlvinB skrev:Jaha! Det är här problemet ligger.
Vi vill ju beräkna ytintegralen
När vi har är det inte så lätt, men vi kan omvandla det hela till att integrera över områdets projektion i -planet. Då blir integralen:
där normalen inte längre är en normerad normal, utan den ges av:
(Detaljerna om vad som egentligen händer här kan du förmodligen läsa om i din kursbok eller denna tråd. Fråga gärna mer också om det är något du inte förstår.)
Sätt nu in i det jag skrev ovan och se hur långt du kommer.
Vad gör jag med "z" i rött 🙄
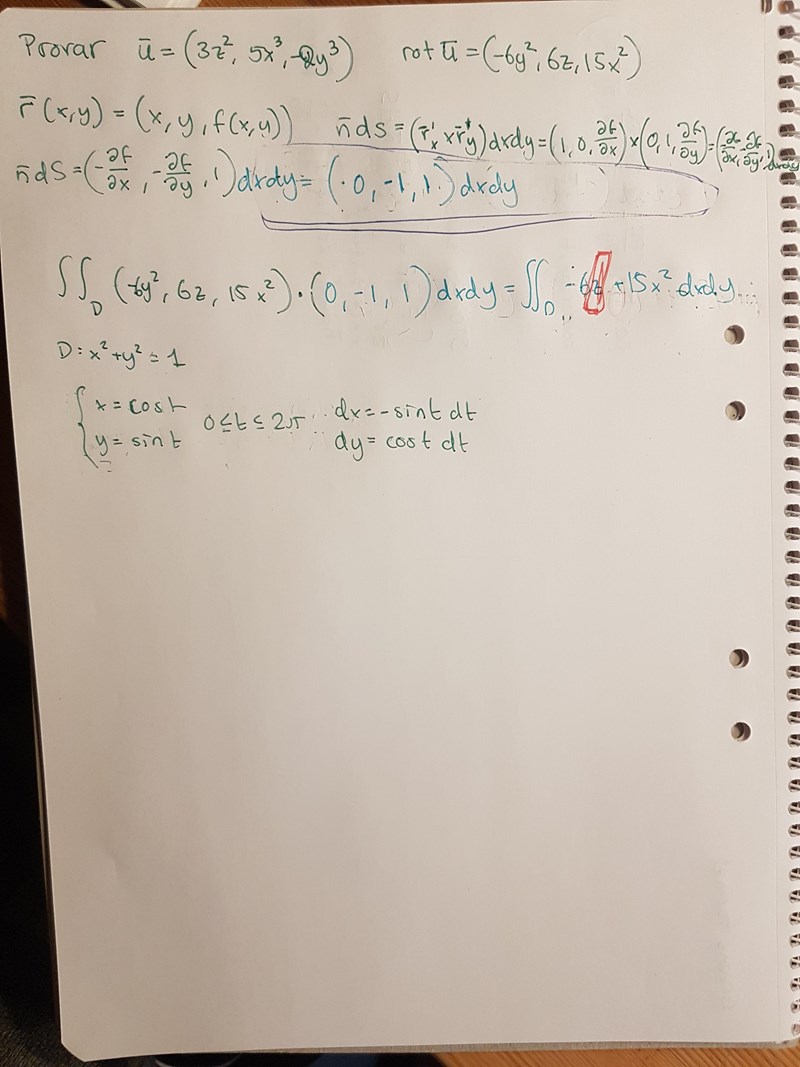
AlvinB skrev:Du skall ju parametrisera ytan, inte vektorfältet (?)!
Ytan är ju planet . Normalvektorn blir då:
Vad blir då integralen?
Vi skrev nog samtidigt för det var dit jag kom 🙂, men fick ett z med som jag inte vet vad jag ska göra med
Svårt att komma på om det är första gången, men lösningen är enkel. :-)
På ytan är ju , så byt ut mot !
AlvinB skrev:Svårt att komma på om det är första gången, men lösningen är enkel. :-)
På ytan är ju , så byt ut mot !
😂🤦♀️👍🙏
AlvinB skrev:Svårt att komma på om det är första gången, men lösningen är enkel. :-)
På ytan är ju , så byt ut mot !
Ser det ok ut nu? Det finns inget facit pga att det bara var hittepå för att försöka få grepp om det.
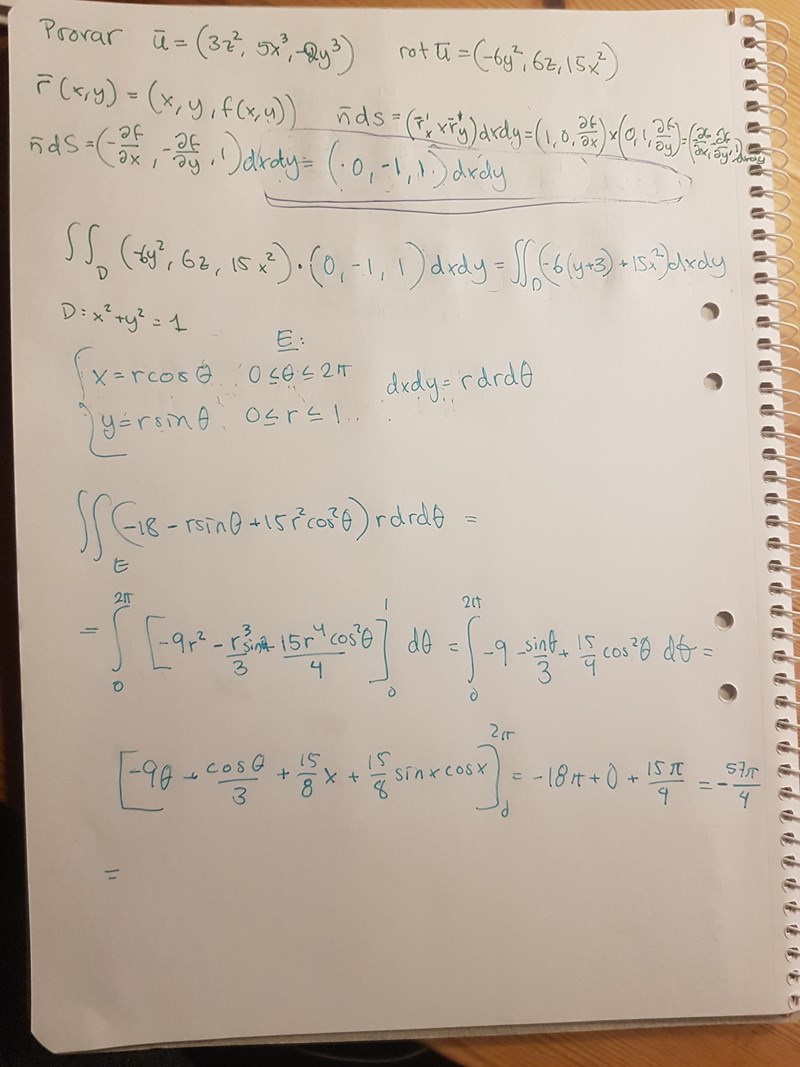
Det är rätt! Bra jobbat!
En annan sak jag kom att tänka på nu är att vi kan göra den riktiga uppgiften på samma sätt och då slippa räkna ut ellipsens halvaxlar.
Vi får ju:
Området :s projektion i -planet (det jag betecknar med ) är en cirkel med radie ett, och alltså får vi att integralen blir lika med .


