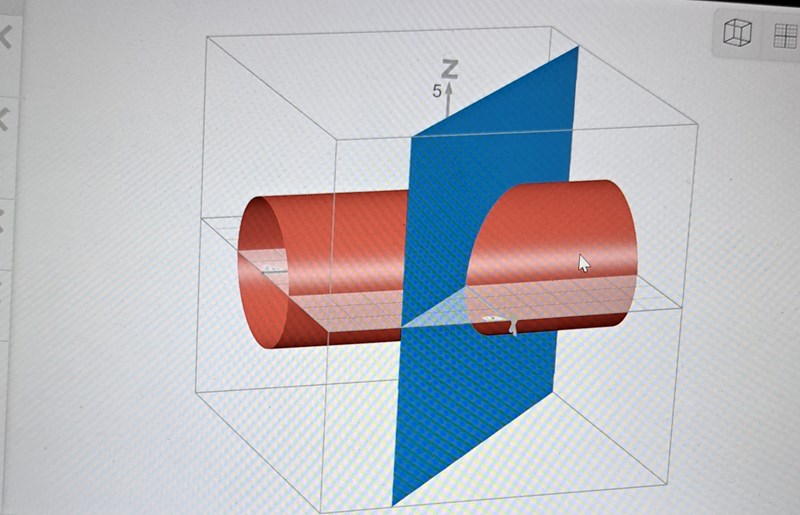
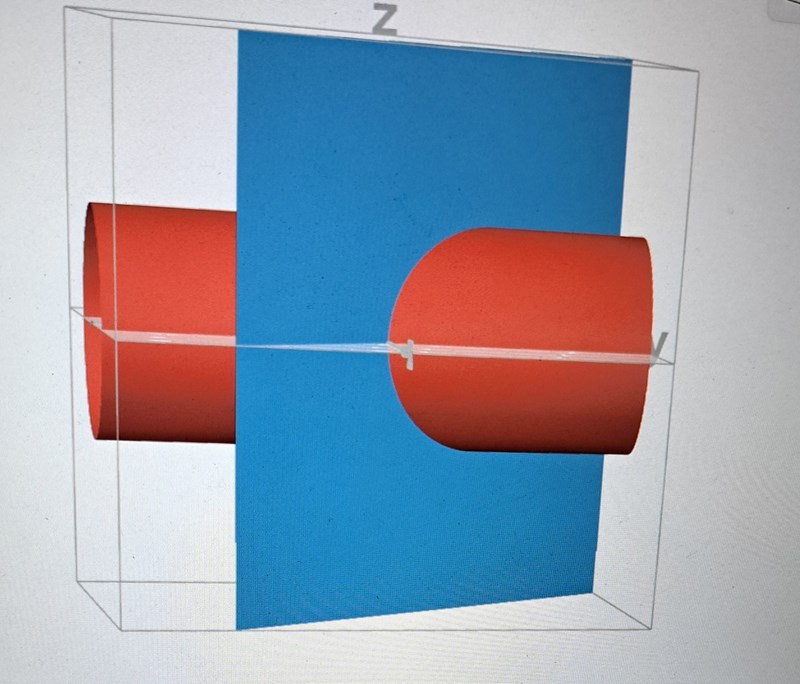
Stokes sats för att beräkna linjeintegralen
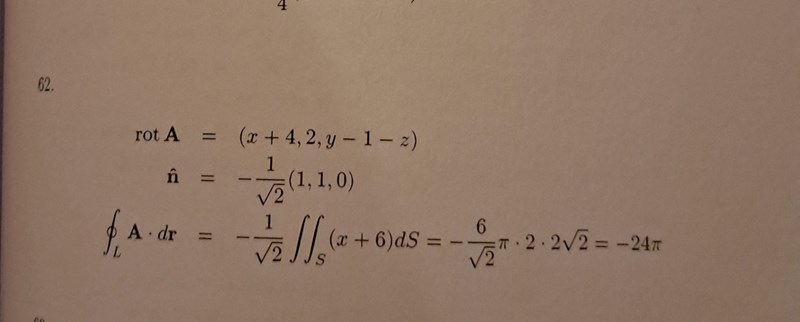


I den första bilden är det lösningsförslag till uppg 62 och jag förstår inte varför x inte räknas med i integralen samt var de får 2*2*sqrt(2)*pi ifrån? Jag gissar att det är ellipsens area. Men hur får man fram denna ellips utifrån hur jag försökte lösa ekvationssystemet i andra bilden? En annan sak jag undrar över är det här med enhetsnormalen, facit använde sig av -1/sqrt(2)(1,1,0) vilket verkar komma ifrån planet. Men varför normerar de den? Ibland är dS=n(hatt) dS och ibland är det dr(u,v) /du×dr(u,v)/dv.
Ytan av en ellips är , där a och b är halvaxlarna.
Här är a = 2 och b = . Rita en (snygg) figur och använd metoden.
Pga av symmetrin så integrerar termen med x till noll.
Du behöver förstå i vilken riktning som kurvintegralen skall utföras och använda högerhandsregeln för att bestämma rätt normalriktning när du skall använda Stokes.
PATENTERAMERA skrev:Ytan av en ellips är , där a och b är halvaxlarna.
Här är a = 2 och b = . Rita en (snygg) figur och använd metoden.
Pga av symmetrin så integrerar termen med x till noll.
Du behöver förstå i vilken riktning som kurvintegralen skall utföras och använda högerhandsregeln för att bestämma rätt normalriktning när du skall använda Stokes.
Men hur får du a=2 och b=2sqrt(2)? Vilken figur utgår du ifrån?
Det här med symmetri för x så att integralen av x blir 0 förstår jag inte. Det här med rätt normalriktning mha högerhandsregelm vet jag inte hur du menar man ska bestämma . Vi har ju givet att punkten (2,0,0) är (0,0,1) och det är där man kan se om orienteringen är moturs eller medurs, men hade svårt att rita den.
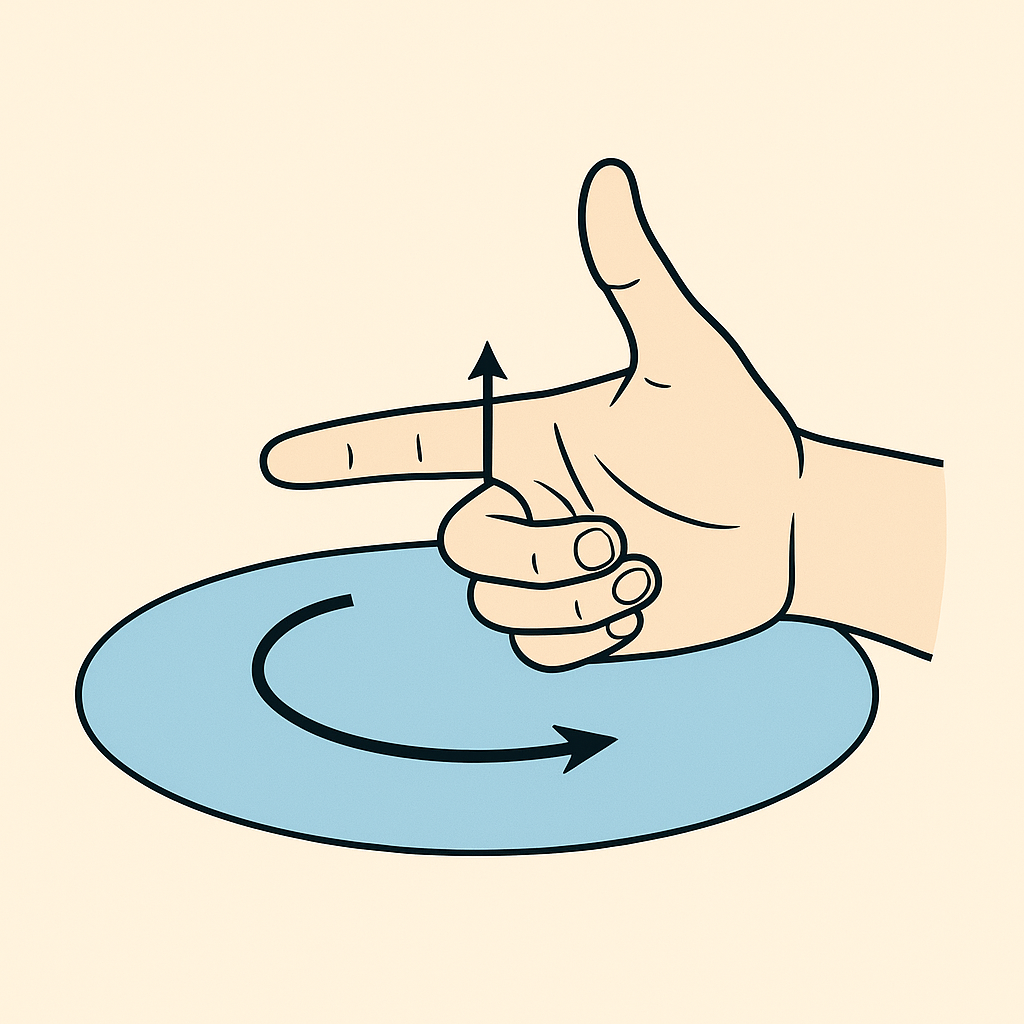
Börja med orienteringen. Var är (2, 0, 0)? Rita in vektorn (0, 0, 1); tänk dig att det är hastigheten hos en bil som kör runt ellipsen. Åt vilket håll runt ellipsen rör sig bilen? Vilken riktning på normalen får man då av högerhandsregeln?
Visa spoiler
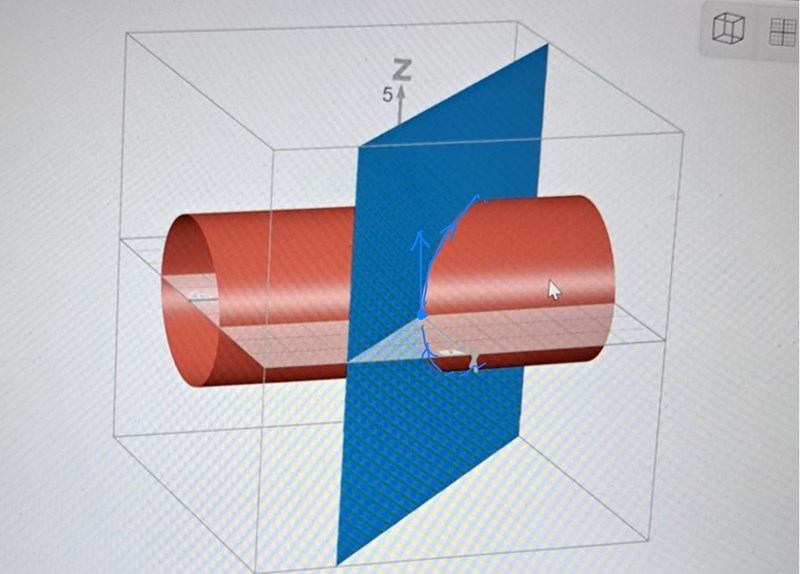
PATENTERAMERA skrev:Visa spoiler
Den här blåa uppåtritade tangentvektor är alltså (0,0,1)?
Ja, en enhetsvektor i z-riktningen.
PATENTERAMERA skrev:Ja, en enhetsvektor i z-riktningen.
Om vektorn är där , hur kan den samtidigt vara i punkten (2,0,0) som är i xy-planet? När det gäller dS riktnikgen så är den väl uppåt då tangentvektor pekar i z-led och mha högerhandsregeln så blir riktningen på kurvan L moturs
(2, 0, 0) är punkten på ellipsen där tangentvektorn till ellipsen är (0, 0, 1).
Det är lite svårt att förstå vad du menar med moturs.
Tangentvektorn visar bara i vilken riktning som ellipskurvan skall genomlöpas. Det är inte normalen till ytan. När du insett vilken riktning som kurvan genomlöpes så kan du lista ut vilken normal som gäller med högerregeln.
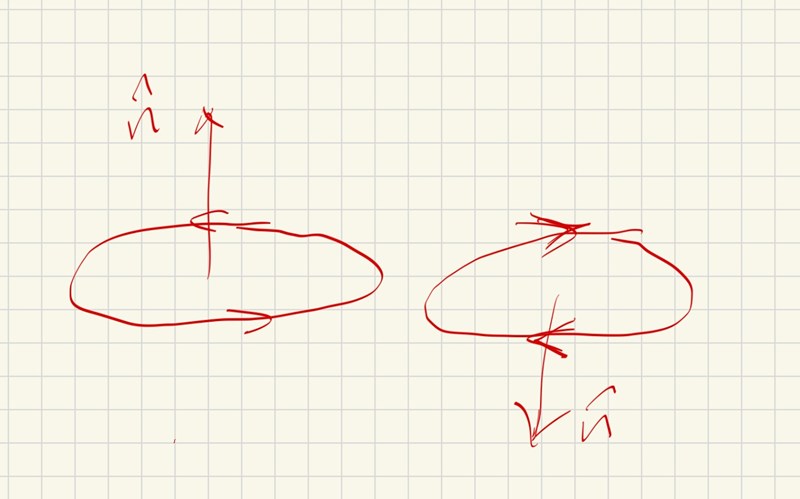
PATENTERAMERA skrev:(2, 0, 0) är punkten på ellipsen där tangentvektorn till ellipsen är (0, 0, 1).
Det är lite svårt att förstå vad du menar med moturs.
Tangentvektorn visar bara i vilken riktning som ellipskurvan skall genomlöpas. Det är inte normalen till ytan. När du insett vilken riktning som kurvan genomlöpes så kan du lista ut vilken normal som gäller med högerregeln.
Hm jag förstår inte kopplingen mellan dina två figurer , tangentvektor och punkten.
Obs detta är bilder som är tänkta att illustrera ett mera allmänt fall och inte precis vårt fall. Nedan visar jag hur man kan illustrera hur orienteringen med en tangentvektor till kurvan.
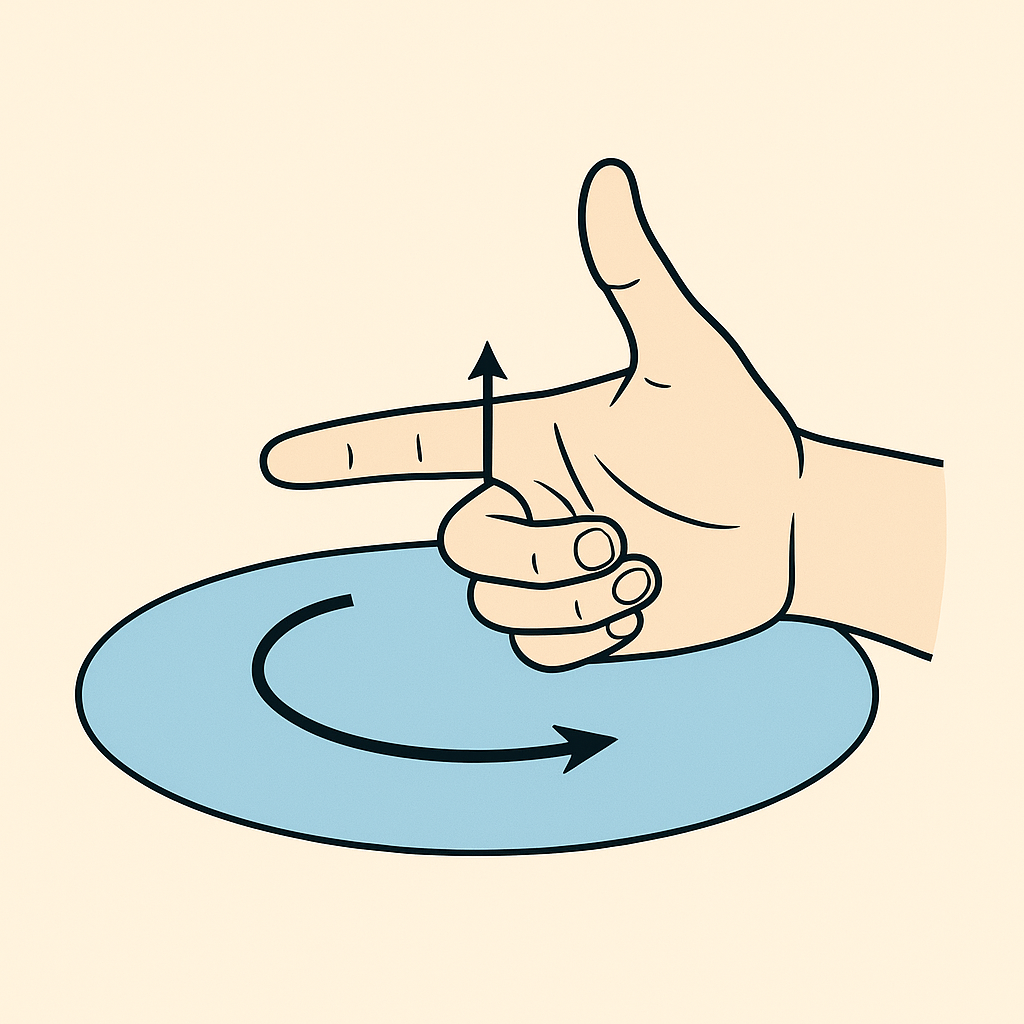
PATENTERAMERA skrev:Obs detta är bilder som är tänkta att illustrera ett mera allmänt fall och inte precis vårt fall. Nedan visar jag hur man kan illustrera hur orienteringen med en tangentvektor till kurvan.
Okej men såsom du ritade tangentvektor i förra bilden #6 så är det medurs. Då måste normalen vara riktad nedåt enligt högerhandsregeln
Ja, normalen skall ha samma riktning som (-1, -1, 0).
PATENTERAMERA skrev:Ja, normalen skall ha samma riktning som (-1, -1, 0).
Detta är alltså planets normalvektor. Varför normaliserar man normalen ? I #2 så sa du att man integrerar x till 0. Varför gör man det?
Var får de ellipsens halvaxlar ifrån? Chat ser området D: x2+z2<=4 som en cirkel i xz planet. Då räknade den ut arean av en cirkel vilket ger samma svar som facit.
Nja, arean av en cirkel med radien 2 är 4pi. Inte 4•sqrt(2)pi.
Men om du har svårt att visualisera halvaxlarna så kan du gå ”back to basics”.
Parametrisera ellipsytan med x och z som parametrar.
r(x, z) = (x, 2 - x, z). Med x2 + z2 4.
dS = (+/-)(dr/dx)x(dr/dz)dxdz. Tecknet väljs så att dS har samma riktning som (-1, -1, 0).
PATENTERAMERA skrev:Men om du har svårt att visualisera halvaxlarna så kan du gå ”back to basics”.
Parametrisera ellipsytan med x och z som parametrar.
r(x, z) = (x, 2 - x, z). Med x2 + z2 4.
dS = (+/-)(dr/dx)x(dr/dz)dxdz. Tecknet väljs så att dS har samma riktning som (-1, -1, 0).
Ja asså jag ser inte riktigt hur det blir en ellips förutom att du säger det. Desmos visade inte den ellips figuren jag var ute efter. Men ok det blir en ellips när skärningen mellan cylinder och planet uppstår , frågan är hur vi bestämmer den mha de ekvationerna vi har? din parametrisering är ingen ellips tror jag eller så missförstår jag den. Ekvationen x^2+y^2<=4 är väl en cylinder och ingen ellips. jag vet hur man bestämmer halvaxlar för en ellips , men då behöver man veta hur den ekvationen ser ut.
Ja i detta fall blir dS positivt ty riktningen på normalen är negativt. Sen tror jag att det är n(hatt) dS som är mer korrekt än ndS, men undrar när den ena gäller och den andra gäller?
Notera att cirkelskivan du nämner bara är parameterdomänen här.
Ellipsen får du genom paramtriseringen r(x, z) där x och z skall ligga inom ovan nämnda domän.
PATENTERAMERA skrev:Notera att cirkelskivan du nämner bara är parameterdomänen här.
Ellipsen får du genom paramtriseringen r(x, z) där x och z skall ligga inom ovan nämnda domän.
Parametriseringen av ellipsen blir (rcosv, 2-2rcosv,rsinv) om man inför polära koordinater till x^2+z^2<=4. Men hur får man halvaxlarna?
Om du parametriserar så behöver du inte bry dig om det utan behöver bara integrera på vanligt sätt.
PATENTERAMERA skrev:Om du parametriserar så behöver du inte bry dig om det utan behöver bara integrera på vanligt sätt.
Ja ok. Men facit normerade n , man måste inte det eller?
Använd formeln för dS som jag skrev i #18. Tänk på att du nu valt v och r som parametrar dock.
dS är en liten vektor som associeras med ett litet ytelement.
dS är riktad så att det är en normalvektor till ytelementet.
Beloppet av dS är lika med ytelementets area dS. dS = |dS|.
Vi kan skriva dS = (dS/dS)dS = ndS, där n = dS/dS är en enhetsvektor.
Om du har en parametriserad yta så kan du räkna ut ett lokalt dS med den formel som beskrevs i #18.
PATENTERAMERA skrev:dS är en liten vektor som associeras med ett litet ytelement.
dS är riktad så att det är en normalvektor till ytelementet.
Beloppet av dS är lika med ytelementets area dS. dS = |dS|.
Vi kan skriva dS = (dS/dS)dS = ndS, där n = dS/dS är en enhetsvektor.
Om du har en parametriserad yta så kan du räkna ut ett lokalt dS med den formel som beskrevs i #18.
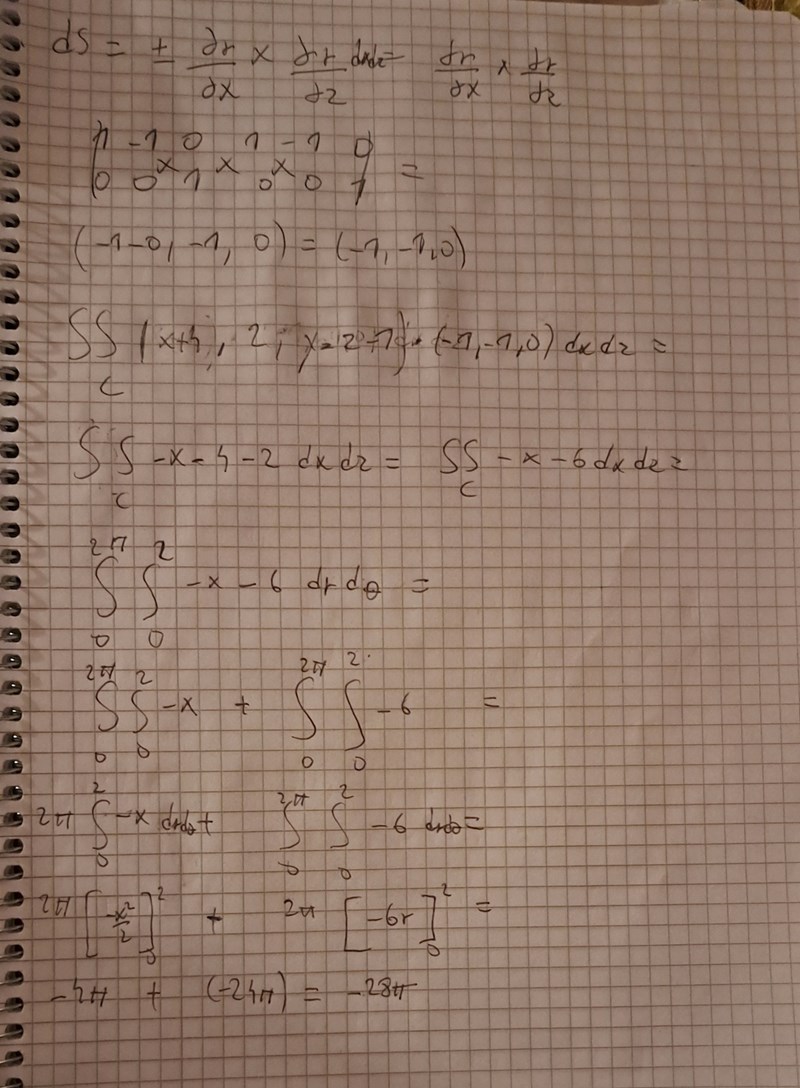
Rätt svar är inte -28pi
Du har , sedan går du över till polära koordinater, men då gäller x = rcosv och dxdz = rdrdv.
Tillägg: 24 sep 2025 18:38
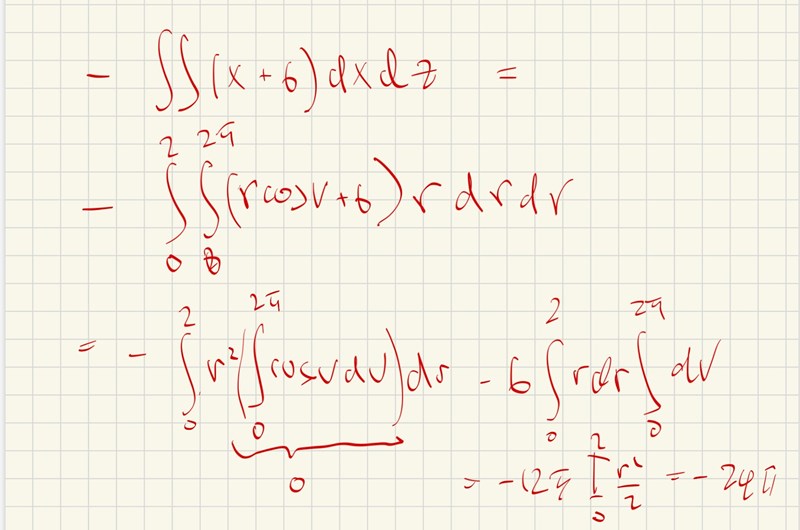
PATENTERAMERA skrev:Du har , sedan går du över till polära koordinater, men då gäller x = rcosv och dxdz = rdrdv.
Tillägg: 24 sep 2025 18:38
Ja nu blev det rätt.