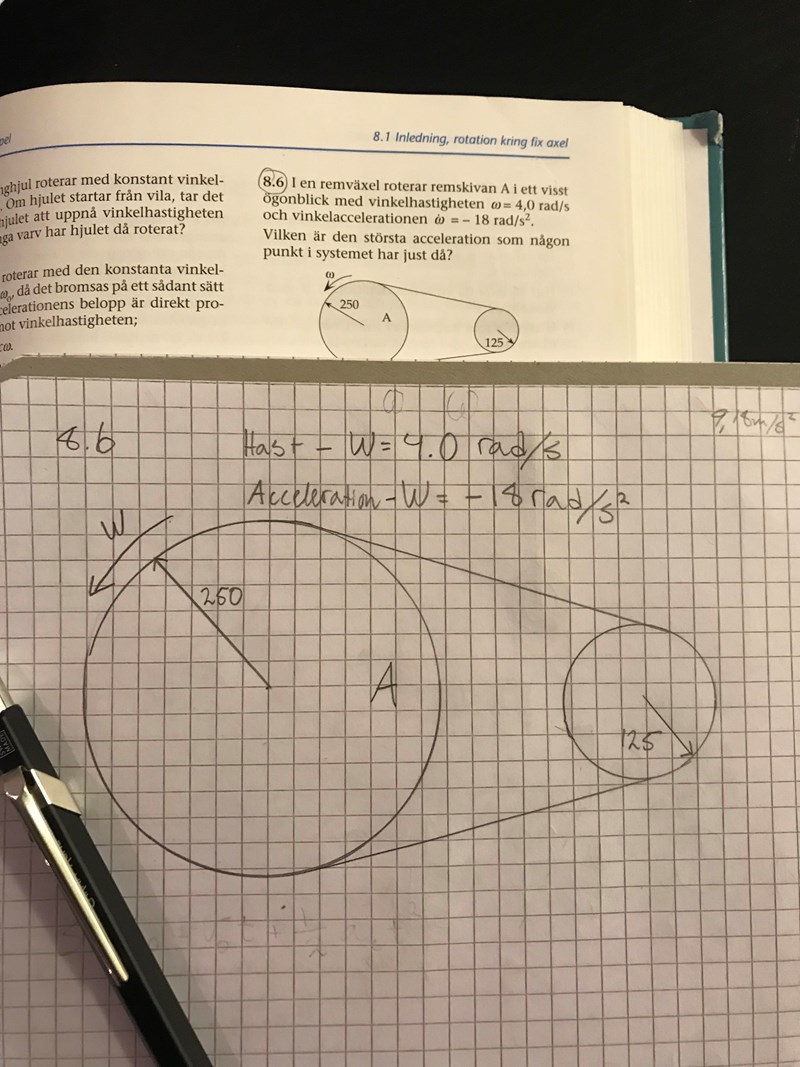
Största acceleration i remväxel
God afton!
Jag har en uppgift som lyder:
"I en remväxel roterar remskivan A i ett visst ögonblick med vinkelhastigheten O=4,0rad/s och vinkelaccelerationen är O=-18rad/s^2.
Vilken är den största accelerationen som någon punkt i systemet har just då?"
Övrig angiven info är att den större remskivan (A) har radien 250mm och den mindre 125mm.
Hur går jag tillväga för att lösa denna uppgift?
Tacksam för svar.
Mvh.
John
Välkommen till Pluggakuten!
Standadrfråga 1a: Har du ritat?
Smaragdalena skrev:Välkommen till Pluggakuten!
Standadrfråga 1a: Har du ritat?
Ja, det har jag.
Kan du lägga upp bilden här, så att vi också kan se den?
Vad har du för samband mellan hastigheterna för olika delar av systemet?
Smaragdalena skrev:Vad har du för samband mellan hastigheterna för olika delar av systemet?
Det enda jag kan anta är att det mindre hjulet roterar dubbelt så fort när det är hälften så stort som hjulet A
Kan du ladda upp en bild på facit?
J.markstrom skrev:Smaragdalena skrev:Vad har du för samband mellan hastigheterna för olika delar av systemet?
Det enda jag kan anta är att det mindre hjulet roterar dubbelt så fort när det är hälften så stort som hjulet A
Vad menar du med dubbelt så fort? Är det rotationshastigheten, eller är det hastigheten för en punkt på periferin?
Syftade på rotationshastigheten, eller tänker jag helt fel nu?
Du tänker rätt. Periferihastigheten måste vara densamma, eftersom hela remmen har samma fart (men inte hastighet).
Vad hittar du för formler som verkar relevanta? Skriv vad formlerna handlar om också, inte bara en bokstavssallad!
Rullningsvillkoret V=r*O , för att ta fram hastigheten för A och genom det använda V för att räkna ut vinkelhastigheten i det mindre hjulet?
Låter vettigt. Eftersom vi har en ninkelacceleration, innebär det att vinkelhastigheten inte är konstant, utan remmens hastighet minskar med tiden. Stämmer det när du sätter in siffror?
Det finns två accelerationer, vinkelräta mot varandra, vars vektorsumma är störst runt lilla hjulet.
- Centripetal-accelerationen:
- Remmens retardation: Den är ju samma runt lilla och stora hjulet 18*0.25=4.5m/s2
Det är sant..
Huruvida sifforna stämmer vet jag inte, Får ut att V=1m/s (för A) och att O=8rad/s (för det mindre hjulet) men det innebär att om jag lägger in det värdet i a=r*O får jag bara ut att O=1..
Är så himla osäker på hur jag skall gå tillväga
Det finns två accelerationer, vinkelräta mot varandra, vars vektorsumma är störst runt lilla hjulet.
- Centripetal-accelerationen:
- Remmens retardation: Den är ju samma runt lilla och stora hjulet 18*0.25=4.5m/s2
Eftersom vektorerna är vinkelräta, använder du sedan Pythagoras...
Nu!!
Tusen tack för hjälpen