Största möjliga area på en rektangel
Hej, jag har en fråga jag börjat räkna på, men har fastnat och vet inte vad mitt nästa steg är
frågan:
En punkt P ligger på grafen till funktionen y = x2 ; 0 < x < 2
Punkten P är ett av hörnen i en rektangel, där en av sidorna ligger på
x-axeln och en på linjen x = 2. Bestäm den största möjliga area, som
rektangeln kan ha.
Jag har skissat en modell:
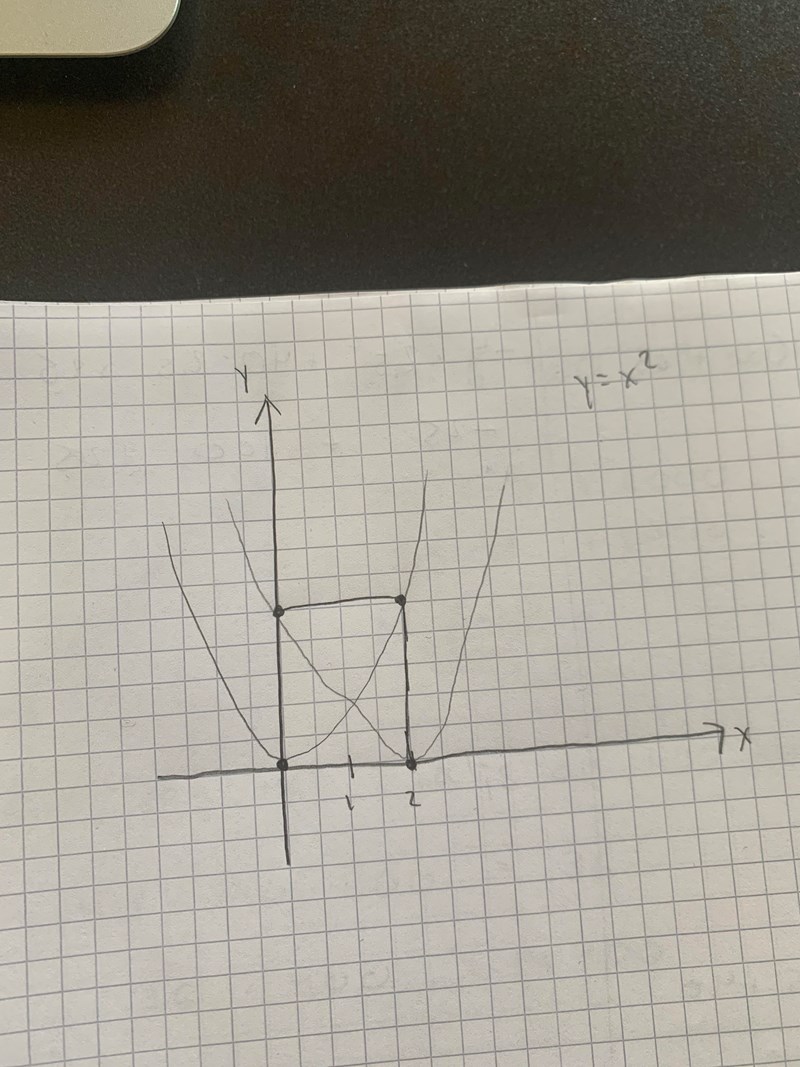
Där man ser rektangeln och de två möjliga graferna till y=x^2. Men hur ska jag nu gå tillväga för att räkna ut den största maximala arean på rektangen? tacksam för svar
y=x2 är en funktion och har ett utseende.
Vad är y(0)=?
Jag ser andra rektanglar som har x-axeln som en sida och x=2 en annan samt ett hörn i P.
Är det alla data som ges i uppgiften?
Din bild ser lite konstig ut. Du borde bara rita ut och .
Sen vill vi teckna ett uttryck för arean av rektangeln som funktion av x.
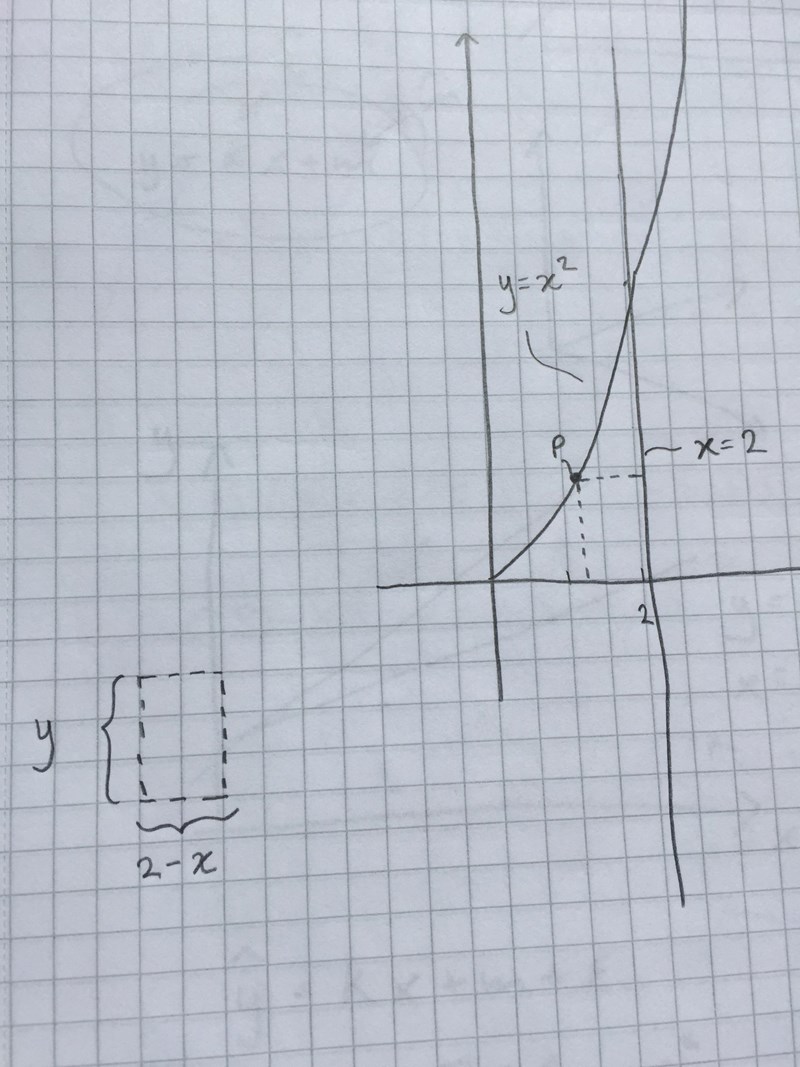
Nu borde det vara mer uppenbart hur du ska göra för att maximera uttrycket?
Denna fråga har varit upp här tidigare: PA-rektangel se om det hjälper dig.
Edit: VoXx har gett dig information som troligen gör att du kommer vidare ...


