Största och minsta värde av flervariabelsfunktion

Du får betrakta randen också.

Laguna skrev:

Du får betrakta randen också.

Hur menas? Vet bara att $f(x,y)=0$ på områdets rand.

Nej, på randen är f(x, y) oftast inte noll. f(1,1) är t.ex. 3.

Laguna skrev:

Nej, på randen är f(x, y) oftast inte noll. f(1,1) är t.ex. 3.

Du har förstås rätt. Men jag begriper inte hur jag ska gå tillväga.

Du får parametrisera randen, alltså hitta funktioner g(t) och h(t) sådana att x = g(t) och y = h(t) för t i något lämpligt intervall, t.ex. 0 till 2 pi.

Sedan uttrycker du f(x,y) i t på randen, och deriverar och håller på igen.

Laguna skrev:

Du får parametrisera randen, alltså hitta funktioner g(t) och h(t) sådana att x = g(t) och y = h(t) för t i något lämpligt intervall, t.ex. 0 till 2 pi.

Sedan uttrycker du f(x,y) i t på randen, och deriverar och håller på igen.

Ah, tack! Menar du något sånt här:

$$\begin{gathered} f(x,y)=x^2+xy+y^2 \iff \\ h\left(t\right)={\cos }^2\left(t\right)+\cos \left(t\right)\sin \left(t\right)+{\sin }^2\left(t\right) \iff h\left(t\right)=\cos \left(t\right)\sin \left(t\right)+1 \end{gathered}$$

Vet dock inte vad jag ska göra därnäst...

Bör jag subtrahera 1 från båda led så att jag får $\cos \left(t\right)\sin \left(t\right)=-1$?

Ett tips är att skriva:

$h(t)=1+\frac{\sin 2t}{2}$

tomast80 skrev:

Ett tips är att skriva:

$h(t)=1+\frac{\sin 2t}{2}$

Tack!!

Laguna skrev:

Du får parametrisera randen, alltså hitta funktioner g(t) och h(t) sådana att x = g(t) och y = h(t) för t i något lämpligt intervall, t.ex. 0 till 2 pi.

Sedan uttrycker du f(x,y) i t på randen, och deriverar och håller på igen.

Jag är hopplös, trodde jag hade hittat största och minsta värde av min funktion f(x,y)=x^2+xy+y^2 men har ju inte alls tagit hänsyn till att det ska vara på området x^2+y^2≤1.

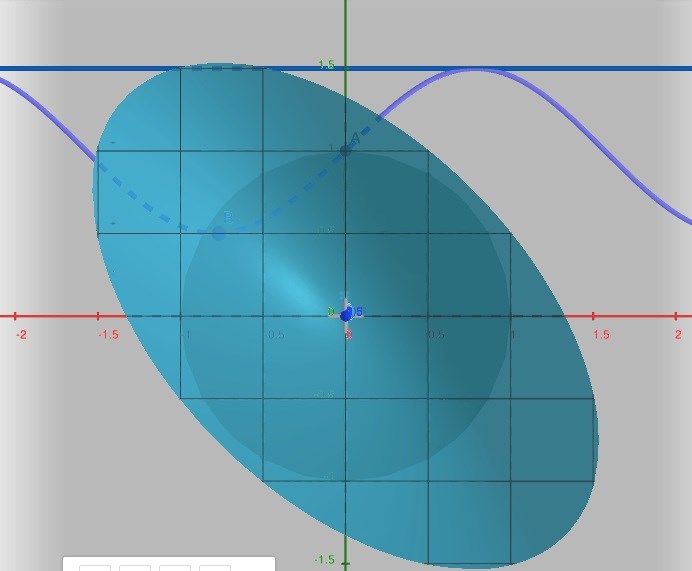
Hittar minsta och största värde på den parametriserade funktionen genom nedanstående figur, men hur ska jag ta hänsyn till randen? Förstår att om området har hörn så sätter man helt enkelt in respektive x- och y-värde i huvudfunktionen och ser vad man får i de olika fallen. Men här har jag ju enhetscirkeln.

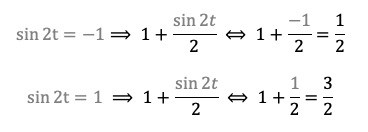
Nedan är min elliptiska funktion, och cirkeln med radie 1 innanför är alltså området där jag ska finna största och minsta värde. Sinusfunktionen som löper tvärs över är den parametriserade funktionen, och den raka linjen ovanför är alltså den övre gränsen (värdet 3/2) som ligger utanför randen, och alltså ej är ett största värde till funktionen? Eller är den det?

Nu inser jag att jag kanske ska derivera den parametriserade funktionen och sätta derivatan lika med noll? På så sätt får jag ju punkten B som är innanför randen, men den andra punkten A (värdet 1) får jag väl enbart genom att titta på figuren? Eller finns det något sätt att beräkna den utan figur?

Och visst är funktionens minsta värde ändå 0 i punkten (0,0)?

Ja, funktionen har sitt minsta värde i punkten (0,0). Och den punkten är en minpunkt!

Funktionen antar sina största värden på randen till området, dvs på kanten till cirkeln.

Låt oss visa det genom att parametrisera randen till cirkeln  med radien 1 så här

$x=cos(\theta),\quad y=\sin(\theta)$

Funktionen $f(x,y)$ blir (ersätt alltså x och y)

$f(\theta)=(\cos(\theta))^2+\cos(\theta)\sin(\theta)+(\sin(\theta))^2=1+\cos(\theta)\sin(\theta)=1+\frac12 \sin(2\theta)$

För t.ex. $\theta=0$ blir funktionnsvärdet i just den punkten  på randen

$f(0)=1$.

Men det är viktigt att du är med på att det är exakt samma sak som att studera punkten $x=1,\, y=0$ dvs, $f(1,0)=1$. Vi har alltså bara parametriserat randen.

Nu gäller det alltså att hitta eventuella extremvärden och jämföra dem med det värde du redan hittat.

Det kan man göra genom att derivera funktionen och ta reda på för vilka $\theta$ derivatan är noll.

Men är man bara intresserad av funktionens största- respektive minsta värde räcker det med att konstatera att det minsta värdet omöjligt kan vara mindre än 1/2 på randen varför punkten (0,0) med värdet 0 är minimum.

Vidare inser vi (eller räknar ut derivatan) att de största värdena antas för $\theta=\frac{\pi}{4},\,\frac{5\pi}{4}$ och så vidare. T.ex.  när $x=\frac{1}{\sqrt{2}},\,y=\frac{1}{\sqrt{2}}$

$f(\frac{\pi}{4})=\frac32$

D4NIEL skrev:

Tack snälla för utförlig förklaring! Det är nästan exakt så som jag svarat i min uppgift och fått fram samma minsta och största värde, men jag är fortfarande färsk på detta, i och med att det största värdet $\frac{3}{2}$, som sagt ser ut att befinna sig helt utanför mitt område som jag trodde att jag skulle hålla mig inom. Begriper liksom inte vad vitsen i såna fall är med det området (syns på min andra figur i förra inlägget).